统计全为1的正方形子矩阵

 题目：

力扣（LeetCode）

登录tzoj

描述

给定一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的正方形子矩阵的个数。

输入

第一行为n和m，表示矩阵的行数和列数(1≤n， m≤300)

之后有n行，每行m个整数，只有0或1组成。

输出

输出全为1的正方形子矩阵个数。

样例输入

3  3

1 0 1

1 1 0

1 1 0

样例输出

7

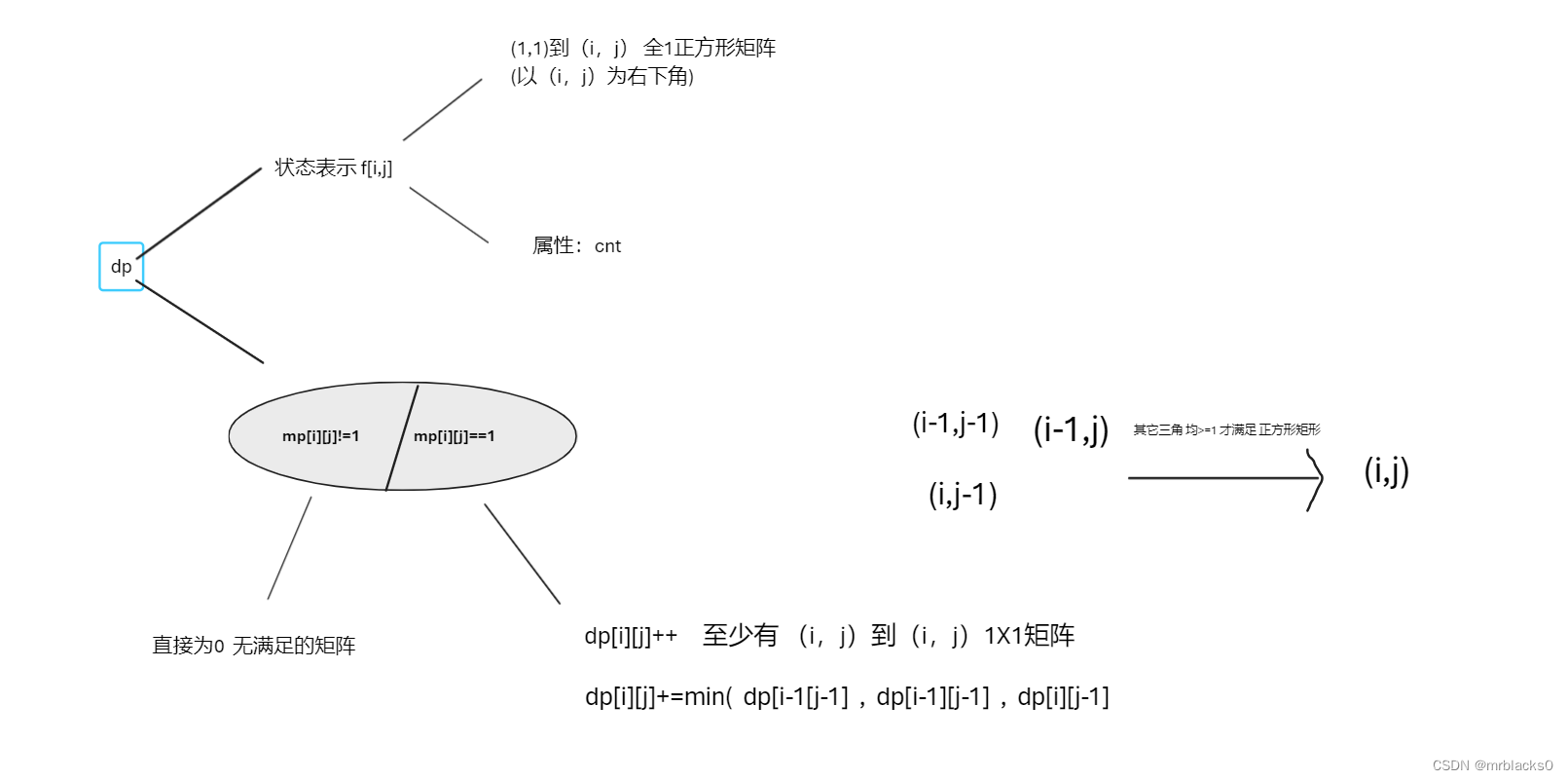
意缘盯真，很容易想到dp(动态规划)问题，但关键在于 f[i,j]的集合表示与关系式（第一次做时 执着于 f[i,j]集合可以直接表示从坐标（0,0）到（i，j）的正方形子矩阵数量总和，但是半天没出来 qwq

但是其实可以换着思路思考，题目给的范围很小，完全可以将f[i,j]看成 (1,1)到f [i,j] 在(i,j)上的矩阵右下角的重复数量（不知道 描述的清楚没，见谅 pwq） 再计数累加。

关键就是状态转移式了 dp[i,j]+=min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j]);因为我们选定了右下角 ，所以只要判断剩下的三个位置，取三点的最小值（数值可能>=1）也就是三点要都是1才会对右下角的个数有贡献。

代码：

#include<bits/stdc++.h>
using namespace std;


typedef long long ll;

const int N=310;
int mp[N][N];
int dp[N][N];

int n,m;
int Min(int a,int b,int c)
{
	return min(min(a,b),c);
}

int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>mp[i][j];
		}
	}
	
	int cnt=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(mp[i][j]==1)
			{
				dp[i][j]+=Min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j])+1;
			} 
			
			cnt+=dp[i][j];
		}
	}
	

	cout<<cnt<<endl;
	return 0;
}

点点赞吧   qwq