传送门:预备队第四周训练
注意: 代码 仅供参考 严谨抄袭
注:代码中的cin,cout 是输入输出 ,和scanf,printf 功能类似。
想要了解可以 先看看 这个。
C++新手入门——标准输出流cout和标准输入流cin语句的超详细解释_c++输出语句-优快云博客
后面代码用到了pair,string,mp等stl的容器,有的同学可能不知道,可自行了解一下。
A:水题 模一下160 就好。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int op;
while(cin>>op)
{
cout<<op%160<<endl;
}
return 0;
}B: 水题 直接 暴力 判断 2^n 应该 也可以,也可以看看我的代码 lowbit 函数有什么作用。
(返回 一个数二进制的末位的值)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
int n;
int lowbit(int x)
{
return x&(-x);
}
int main()
{
while(cin>>n)
{
if(n-lowbit(n)==0) cout<<"ACM"<<endl;
else cout<<"MCA"<<endl;
}
return 0;
}
C:贪心 先砍消耗少的树。
#include<bits/stdc++.h>
using namespace std;
int main()
{
long long n,m,t,i,sum=0;
cin>>n>>m>>t;
int a[n];
for(i=0;i<n;i++)
{
cin>>a[i];
}
sort(a,a+n);
for(i=0;i<n;i++)
{
if(t>a[i])
{
t-=a[i];
sum++;
}
else break;
}
if(sum>=m) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
return 0;
}D:
逆序对数量,冒泡排序 即可 n^2=10000*10000=1e8 时间上恰 不会爆。
#include<bits/stdc++.h>
using namespace std;
const int N=10000;
int a[N];
int b[N];
int n;
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
b[i]=a[i];
}
int cnt=0;
for(int i=0;i<n;i++)
{
for(int j=0;j<n-1;j++)
{
if(a[j]>a[j+1])
{
int t =a[j];
a[j]=a[j+1];
a[j+1]=t;
cnt++;
}
}
}
cout<<cnt<<endl;
return 0;
}
E:
二分 ,不过这题是 数是 从大到小排的,因此二分的条件判断要稍改一下。注意 mid 因为找的数字 是小于等于的 最终位置 靠右 因此 mid=(l+r+1)>>1;
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1000000+10;
int a[N];
int n;
int m;
signed main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
while(m--)
{
int q;
cin>>q;
int l=1;
int r=n;
while(r>l)
{
int mid=r+l+1>>1;
if(a[mid]>=q) l=mid;
else r=mid-1;
}
if(r>n||a[r]!=q) cout<<"None"<<endl;
else cout<<r<<endl;
}
}F:
可以从上往下 dp (也可以从下往上),展示代码是从上往下 。
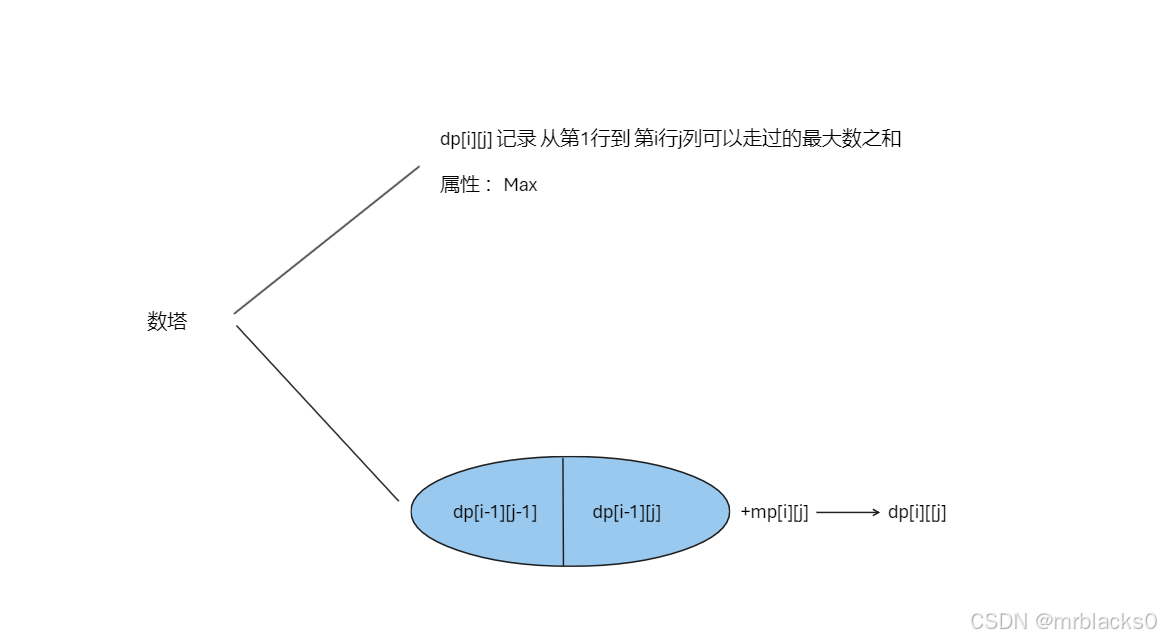
dp 数组 记录 到这个位置的最大数字和,当前位置 由 上方和上方靠右 两个位置 转移而来。
状态转移方程是 dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+map1[i][j];
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int map1[N][N];
int dp[N][N];
int main()
{
int t;
cin>>t;
while(t--)
{
int n,i,j;
cin>>n;
for(i=1;i<=n;i++)
{
for(j=1;j<=i;j++)
{
cin>>map1[i][j];
}
}
memset(dp,0,sizeof(dp));
for(i=1;i<=n;i++)
{
for(j=1;j<=i;j++)
{
dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+map1[i][j];
}
}
int x=0;
for(j=1;j<=n;j++)
{
if(dp[n][j]>x)
{
x=dp[n][j];
}
}
cout<<x<<endl;
}
return 0;
}G:
与上题相比 多了一步 输出 路径,那么dp 完之后 ,只需要 找到 最后 一行 的最大值(dp是 从上往下处理 则不需要这步,直接往下走即可)
往上走,找上方和上右的数是不是到该层 最大的数值和-数值 。
注:代码中 用了 结构体,num是数塔原来的值,maxall是到这个位置最大的数值总和。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=110;
struct in{
int num;
int maxall;
};
in mp[N][N];
int n;
void solve()
{
cin>>n;
memset(mp,0,sizeof(mp));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>mp[i][j].num;
}
}
int mx=-1;
int x,y;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
if(i==1&&j==1)
{
mp[i][j].maxall=mp[i][j].num;
continue;
}
mp[i][j].maxall=max(mp[i-1][j-1].maxall,mp[i-1][j].maxall)+mp[i][j].num;
}
if(i==n)
{
for(int j=1;j<=i;j++)
{
if(mp[i][j].maxall>mx)
{
mx=mp[i][j].maxall;
y=i;
x=j;
}
}
}
}
cout<<mx<<":";
vector<int>a;
a.clear();
while(y!=0)
{
a.push_back(x);
int temp=mp[y][x].maxall-mp[y][x].num;
if(mp[y-1][x-1].maxall==temp)
{
y=y-1;
x=x-1;
}
else
{
y=y-1;
x=x;
}
}
for(int i=a.size()-1;i>=0;i--)
{
cout<<' '<<a[i];
}
cout<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
H:
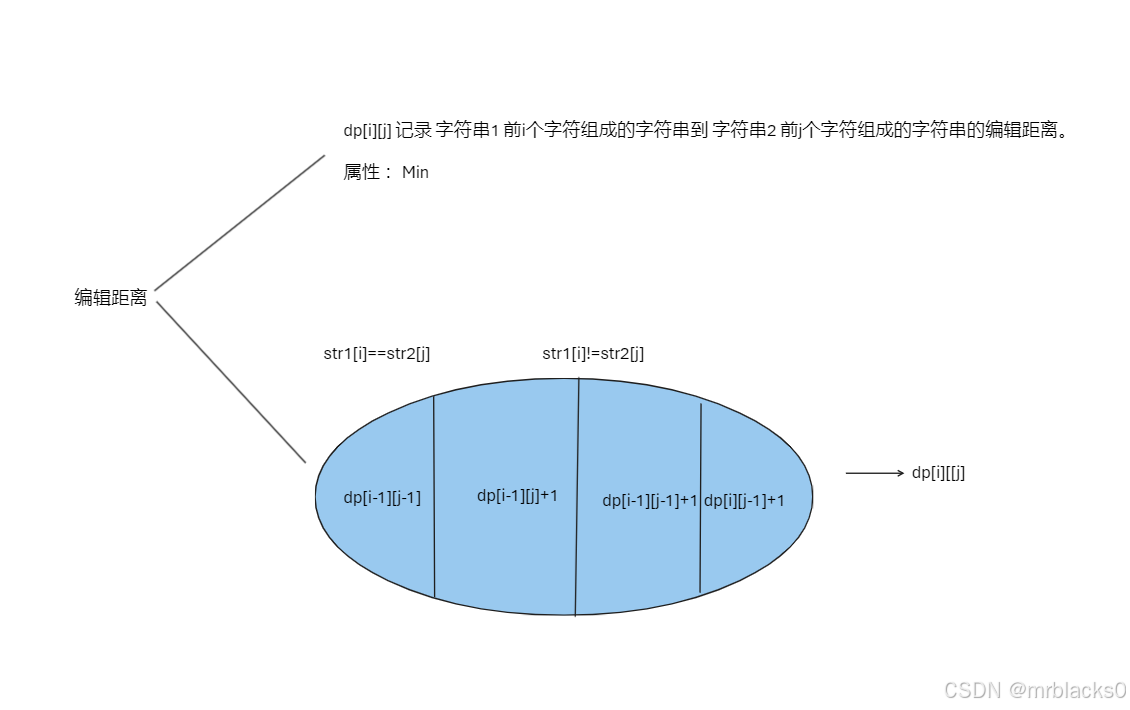
dp[i][j] 状态表示 :dp[i][j] 是 字符串1 前i个字符组成的字符串到 字符串2 前j个字符组成的字符串的编辑距离。
不过 比较特殊的情况就是 i=0或是j=0时的情况,也就是 空字符到字符串的情况,预处理一下。
状态表示:
如果字符串1 第i个字符与 字符串2 第j个字符 相同,就等同于 比较字符串1前i-1的字符串和 字符串2前j-1的字符串,dp[i][j]=dp[i-1][j-1];
如果不同,则处理 增 删 改,的状态:
增加:由字符串1前i-1的字符串增加而来 dp[i][j]=dp[i][j-1]+1;
修改:将最后字符串1 的最后一个字符串修改,dp[i][j]=dp[i-1][j-1]+1;
删除:由字符串1删除一个字符 dp[i][j]=dp[i-1][j]+1;
取三者最大值。
#include<bits/stdc++.h>
using namespace std;
const int N=1030;
char zifu1[N];
char zifu2[N];
int dp[N][N];
int main()
{
while(scanf("%s",zifu1+1)!=EOF)
{
scanf("%s",zifu2+1);
int i,j;
int n,m;
n=strlen(zifu1+1);
m=strlen(zifu2+1);
memset(dp,0,sizeof(dp));
for(j=0;j<=m;j++)
{
dp[0][j]=j;
}
for(i=0;i<=n;i++)
{
dp[i][0]=i;
}
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
if(zifu1[i]==zifu2[j])
{
dp[i][j]=dp[i-1][j-1];
}
else
{
int x;
x=min(dp[i-1][j],dp[i-1][j-1]);
dp[i][j]=min(x,dp[i][j-1])+1;
}
}
}
printf("%d\n",dp[n][m]);
}
return 0;
}I:
与上题 不同的一点是 少了修改这一操作 ,
那只要两个字符串不同的时候 比较 删除 增加状态的操作次数就好。
就是 上题 稍微修改一下。
#include<bits/stdc++.h>
using namespace std;
int n,m;
string x,y;
int f[1100][1100];
int main()
{
cin>>x;
cin>>y;
x=' '+x;
y=' '+y;
int n=x.size();
int m=y.size();
for(int i=0;i<=n;i++)
{
f[i][0]=i;
}
for(int j=1;j<=m;j++) f[0][j]=j;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(x[i]==y[j])
{
f[i][j]=f[i-1][j-1];
}
else
{
int x;
f[i][j]=min(f[i-1][j],f[i][j-1])+1;
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
J:
bfs,每层 都可以 选择上或是下(楼层数>=1)。因为最先走过的楼层步数必然是最少的,开个数组标记一下,防止重复。到了结束位置退出即可。否则输出-1。
pair<int,int> 可以简单理解为 一个存了 两个int 的东西
变量.first访问第一个数,变量.second 访问第二个数。
#include<bits/stdc++.h>
using namespace std;
signed main()
{
pair<int,int>a;
printf("this is input\n");
scanf("%d%d",&a.first,&a.second);
printf("\n");
printf("this is output\n");
printf("%d %d\n",a.first,a.second);
}
//示例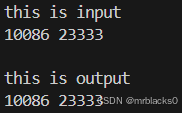
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
typedef long long ll;
const int N = 255;
typedef pair<int, int> pii;
int an[N];
int n,a,b;
int vis[N];
void bfs()
{
queue<pii>q;
q.push({a,0});
vis[a]=1;
while(q.size())
{
auto cur=q.front();
//cout<<cur.first<<endl;
q.pop();
if(cur.first==b)
{
cout<<cur.second<<endl;
return ;
}
for(int i=-1;i<=1;i+=2)
{
int t=i*an[cur.first]+cur.first;
if(t>=1&&!vis[t]&&t<=n)
{
vis[t]=1;
q.push({t,cur.second+1});
}
}
}
cout<<-1<<endl;
}
signed main()
{
cin>>n>>a>>b;
for(int i=1;i<=n;i++)
{
cin>>an[i];
}
bfs();
}K:
数学推导,具体看我推导(字丑勿喷 QWQ)
也可网上搜搜 其它题解。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll N=1000000+10;
ll a[N];
ll c[N];
ll n;
int main()
{
cin>>n;
ll sum=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
c[i]=c[i-1]+a[i];
sum+=a[i];
}
sum/=n;
for(int i=1;i<=n;i++)
{
c[i]-=sum*i;
}
sort(c+1,c+1+n);
ll mid;
if(n%2==1)
{
mid=c[n/2+1];
}
else{
mid=(c[n/2]+c[n/2+1])/2;
}
ll cnt=0;
for(int i=1;i<=n;i++)
{
cnt+=abs(c[i]-mid);
}
cout<<cnt<<endl;
return 0;
}L:
题目给的数组 最大值是 100*100,比较大。如果单纯dfs+回溯时间上不行。
题目找最小的 差值,可以用二分优化时间。
但是回溯还是一个问题,那么我们限定一个区间范围,dfs 搜索是不是有这样的区间 满足可以到终点的路径,这样我们走过的路径是必然合法的,就不需要回溯了。
#include <bits/stdc++.h>
using namespace std;
#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
#define endl "\n"
int n;
int mp[110][110];
int vis[110][110];
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int mn = 200;
int mx = 0;
bool f;
void dfs(int y, int x,int mnn, int mxx)
{
if(f) return ;
if (y == n && x == n)
{
f=1;
return ;
}
for (int i = 0; i < 4; i++)
{
int yy = y + dir[i][0];
int xx = x + dir[i][1];
if (yy >= 1 && yy <= n && xx >= 1 && xx <= n && !vis[yy][xx]&&mp[yy][xx]<=mxx&&mp[yy][xx]>=mnn)
{
vis[yy][xx]=1;
dfs(yy,xx,mnn,mxx);
//vis[yy][xx]=0; 不需要回溯
}
}
}
bool check(int mid)
{
for(int i=mn;i<=mn+mid;i++)
{
if(mp[1][1]<i||mp[n][n]<i||mp[1][1]>i+mid||mp[n][n]>mid+i) continue;
memset(vis,0,sizeof(vis));
vis[1][1]=1;
f=0;
dfs(1,1,i,i+mid);
if(f)
{
return 1;
}
}
return 0;
}
signed main()
{
ios;
cin >> n;
mx=0;
mn=200;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
cin >> mp[i][j];
mn = min(mn, mp[i][j]);
mx = max(mx, mp[i][j]);
}
}
int l =0, r = mx - mn;
while (l < r)
{
int mid = (l + r)>>1;
if (check(mid)) r = mid;
else l = mid + 1;
}
cout << l << endl;
return 0;
}
M:
小故事 :
某帅气同学:学长 有道传送门 还蛮难的 。
出题人:真的吗? 现已加入 第4周周训套餐! QwQ
我的代码思路:map存储两个相互的传送门,bfs拓展路径,注意遇到传送门时需要特殊处理。
因为有种情况是通过传送门a1传送到a2,在a2向外探索,又通过a2传送回a1(可能 a1 离终点更近)。
所以我们不能提前标记 传送过去的a2,只把a1标记掉,因为a1走过了。这样就有余地可以通过a2往回传送。
也可以看看 这篇题解
拯救小Q (多传送门求最短路径问题)(bfs)-优快云博客
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
const int N = 55;
int n, m;
typedef pair<int, int> pii;
int dir[4][2] = {1, 0, 0, 1, -1, 0, 0, -1};
char a[N][N];
int vis[N][N];
int stx, sty, edx, edy;
map<pii, pii> mp;
vector<pii> b[30];
struct in
{
int y, x;
int step;
};
bool check(int y, int x)
{
return y >= 1 && y <= n && x >= 1 && x <= m && !vis[y][x] && a[y][x] != '#';
}
void bfs()
{
queue<in> q;
q.push({sty, stx, 0});
vis[sty][stx] = 1;
while (!q.empty())
{
in cur = q.front();
q.pop();
if (cur.x == edx && cur.y == edy)
{
cout << cur.step << endl;
return;
}
for(int i=0;i<4;i++)
{
int yy=cur.y+dir[i][0];
int xx=cur.x+dir[i][1];
if(check(yy,xx))
{
if(a[yy][xx]>='a'&&a[yy][xx]<='z')
{
vis[yy][xx]=1;
pii t=mp[{yy,xx}];
q.push({t.first,t.second,cur.step+1});
}
else
{
vis[yy][xx]=1;
q.push({yy,xx,cur.step+1});
}
}
}
}
cout << -1 << endl;
}
void solve()
{
cin >> n >> m;
mp.clear();
memset(vis, 0, sizeof(vis));
for (int i = 0; i < 30; i++)
b[i].clear();
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
if (a[i][j] == 'Q')
{
edy = i;
edx = j;
}
else if (a[i][j] == 'L')
{
sty = i;
stx = j;
}
else if (a[i][j] >= 'a' && a[i][j] <= 'z')
{
char temp = a[i][j];
pii cur = {i, j};
if (b[temp - 'a'].size() == 1)
{
pii other = b[temp - 'a'][0];
mp[cur] = other;
mp[other] = cur;
}
else
{
b[temp - 'a'].push_back(cur);
}
}
}
}
bfs();
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while (t--)
{
solve();
}
}额外提供两组 数据:
/*
样例输入
1
5 5
....L
.#a#.
b#Q#.
##b##
..a..
答案 6
*/
/*
1
5 5
....L
.###.
a#Q#.
##.##
a.b.b
答案 12
*/
END




















 186
186

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








