Reinforcement Learning - An Introduction memo

1.MDP(Markov Decision Processes)

finite MDP: finite state space&finite action space

transition probabilities：p(s′ | s, a) = Pr{S_t+1 = s′ | S_t = s, A_t = a}

r(s, a, s′) = E[R_t+1 | S_t = s, A_t = a, S_t+1 = s′]

2.Value Functions

state-value function: v_$\pi$(s)=E_$\pi$[G_t|S_t = s] = E_$\pi$[$\sum_{k=0}^{\infty}\gamma ^{k}R_{t+k+1}$| S_t = s]

action-value function: q_$\pi$(s, a) = E_$\pi$[G_t|S_t = s, A_t = a] = E_$\pi$[$\sum_{k=0}^{\infty}\gamma ^{k}R_{t+k+1}$| S_t = s, A_t = a]
G_t: return (cumulative discounted reward) following t
R_t: reward at t, dependent, like S_t, on A_t−1 and S_t−1
G_t = $\sum_{k=0}^{\infty}\gamma ^kR_{t+k+1}$

v_$\pi$, q_$\pi$: v_$\pi$(s) = $\sum_a\pi(a|s)q_\pi(s, a)$ q_$\pi$(s, a) = $\sum_{s'}p(s'|s, a)[r(s, a, s')+\gamma$v_$\pi$(s’)]
$\pi(a|s)$: probability of taking action a when in state s

Bellman Equation for v_$\pi$: v_$\pi$(s) = $\sum_{a} \pi(a|s)\sum_{s'}p(s'|s, a)[r(s, a, s')+\gamma v_\pi(s')$]
Bellman function => learn v_$\pi$

Bellman Equation for q_$\pi$: q_$\pi$(s, a) = $\sum_{s'}p(s'|s, a)[r(s, a, s')+\gamma\sum_{a'}\pi(a' | s')q_\pi(s', a')]$

3.Policy Evaluation

policy evaluation: compute v_$\pi$ for policy $\pi$
Iteration policy evaluation:
1. For state s, the initial v₀ is chosen arbitary(terminal state 0)
2.Successive approximation is obtained by using the Bellman Equation:
v_k+1(s) = E$_\pi$[R_t+1+$\gamma$v_k(s_t+1) | S_t = s]
code:

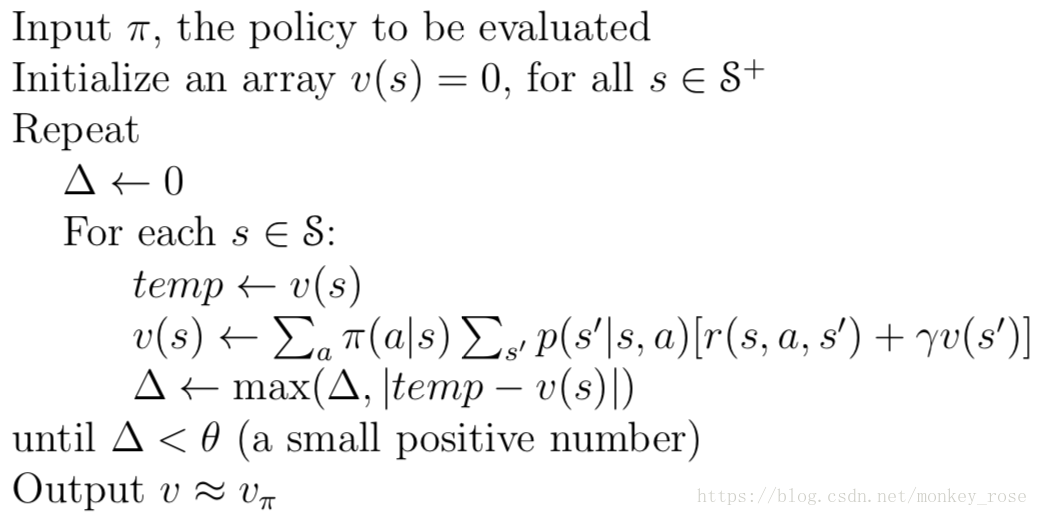
4.Policy Improvement

policy improvement: evaluate policy to find better policies

greedy policy $\pi'$: $\pi'$(x) = arg $\mathop{}_{a}^{max} q_\pi(s, a)$
The greedy policy takes the action that looks best in the short term—after one step of lookahead—according to v$_\pi$.

5.Policy Iteration&Value Iteration

policy iteration

code:

an example:

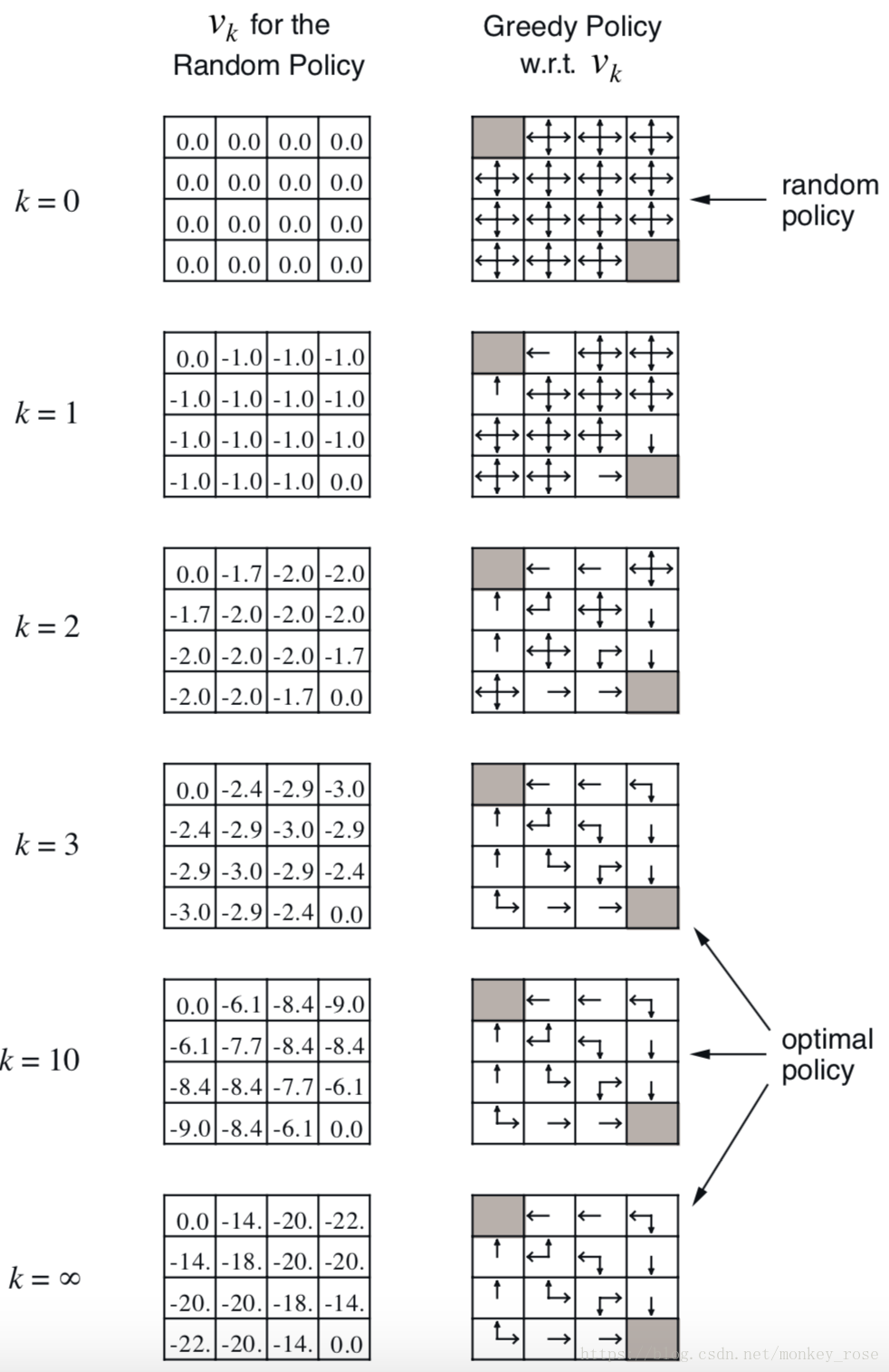
value iteration

It can be written as a particularly simple backup operation that combines the policy improvement and truncated policy evaluation steps, more efficient.

v_k+1(s) = $\mathop{}_{a}^{max}$ E[R_t+1+$\gamma$v_k(S_t+1) | S_t = s, A_t = a]

code:

Q-Learning

Initialize Q(s,a) arbitrarily
Repeat (for each episode):
    Initialize s
    Repeat (for each episode):
        Choose a from s using policy derived from Q(e.g.,ε-greedy)
        Take action a, observe r, s'
        Q(s, a)←Q(s, a) + α[r + γmaxQ(s', a')-Q(s, a)]
        s←s'
    util s is terminal

Evaluation:

update Q-table, in every episode, Q(s, a) is the value in the table, max_a’Q(s’, a’) is the max approximation for Q(s’)

decision policy:

ε-greedy: ε = 0.9, choose the best action for 90%, choose others randomly for 10%