运放电路噪声

1 电阻噪声

        放大器电路的噪声性能受到电阻器约翰逊噪声的极大影响：电源电阻和反馈电阻器，电阻器的戴维宁噪声模型由与噪声电压串联的无噪声电阻器构成。

图1 

        噪声电压与电阻、带宽和温度（开尔文）的平方根成比例。电阻的理论噪声是“白噪声”，这意味着噪声在频率上均匀分布。它在每个等带宽的频带内具有相等的噪声。
        每 1Hz 频带内的噪声总和等于每个噪声的平方和再开方。通常将伏/平方根赫兹作为频谱密度。对于 1Hz 带宽，这个数值就等于噪声大小。对于白噪声，频谱密度与带宽的平方根相乘，可以计算出每 1Hz 频带的随机贡献之和。要测量和量化总噪声，需要限制带宽（图2）。如果不知道截止频率，就不知道要对多少噪声求积分。 

图2

         电阻器噪声也服从高斯分布，高斯分布是描述其振幅分布的概率密度函数。它之所以服从高斯分布，是因为它是由大量小的随机事件产生的。交流(AC) 噪声的均方根 (RMS) 电压等于±1 σ 的振幅分布（图 3）。对于 1V RMS 噪声，瞬时电压在 ±1V 范围内的概率为 68%(±1σ)。一种常见的误解是将白噪声与高斯分布关联或等同起来，但它们是不相关的。例如，滤波电阻器噪声不是白噪声，但仍然服从高斯分布。二进制噪声肯定不服从高斯分布，但它可能是白噪声。电阻器噪声是白噪声并且服从高斯分布。

图3 

        纯粹主义者会大声斥责高斯噪声没有定义的峰间值 – 他们说它是无限的。确实，高斯分布的两侧是无限伸展的，因此理论上来说，任何电压取值确实都是有可能的。然而，在实际中噪声尖峰超过RMS 值 ±3 倍的可能性非常小，许多人用大约 RMS 的六倍来表示峰峰值。通过使用RMS的八倍值可以使您在添加一个较大的额外保护频带的同时免受极大程度的更改该值的风险。

        两个串联电阻器的噪声电压随机求和，其结果与这两个电阻器值之和的噪声相同。类似地，并联的电阻器噪声之和等于其并联电阻产生的噪声。如果不是这样，那么就会出问题：考虑将一个物理电阻器平分成两份，然后将其串联或并联。但一切都正常。
        放在您的桌子上的高阻值电阻不会因为无限的自生噪声电压而产生电弧和火花。杂散并联电容将限制带宽和总电压。类似地，可以想象绝缘体上产生的高噪声电压也会被杂散电容和其周围的导体电阻分流。

2 同相放大噪声

        将输入源建模为具有串联电阻的电压噪声源（图 4），众所周知，信号源的内阻 RS 具有与其电阻的平方根成比例的噪声（图5中的直线）。低噪电阻的目标是，在既有的电压噪声源的基础
上，带来尽可能小的额外噪声。

图4 

        如图4所示，放大器噪声建模为与一个输入串联的电压噪声和与每个输入连接的电流噪声源。将电压噪声视为失调电压的时变分量。类似地，电流噪声是输入偏置电流的时变分量，每个输入上一个。
        图5显示了两个运算放大器的电路的总输入相关噪声 – 双极结型晶体管 (BJT) 输入 OPA209 和结型 FET (JFET) 输入 OPA140。每个都显示为与 25°C 下电源电阻的噪声相关。三个噪声源通过每个运算放大器的平方和根值求和。

图5

        当电源电阻减小时，其伴随的约翰逊噪声会降低（电阻平方根的倒数），在某一点，放大器的电压噪声起主导作用。总噪声会变平，其值等于放大器的电压噪声。当电源电阻增大时，流过电源电阻的电流噪声会产生以线性方式增加的噪声，从而以更快的速度增加，并最终超过电源电阻的噪声。因此，在高电源电阻下，电流噪声的影响起主导作用。
        低噪放设计中的巨大挑战主要来源于对电源电阻的要求—尽可能低于2kΩ。该区域中的较低电源电阻噪声需要具有极低电压噪声的放大器。一般而言，BJT 输入放大器在该范围内非常出色。还请注意，图5 中 OPA209 的总噪声最接近位于“极佳位置”的电源电阻噪声。这个具有出色噪声性能的电源电阻产生条件为 RS = VN / IN 。
        当电源电阻高于 20 kΩ 左右时，FET 输入放大器产生的额外噪声很小。除非您达到几千兆欧姆的电源电阻，否则 FET 运算放大器的电流噪声通常不会产生重要的作用。准则：电源电阻低于
10kΩ 时，低噪声 BJT 放大器通常会产生较低的噪声。在高于大约 10kΩ 时，FET 或互补金属氧化物半导体 (CMOS) 运算放大器可能具有优势。
        反馈网络 R1 和 R2 也会产生噪声，但一般可以使其变得无关紧要。如何实现？简单说来，如果 R1 和 R2 的并联组合是 RS 的十分之一（或更小），那么它们对总噪声的提升将不到 10% (<1 dB)。无论为了达到闭环增益而采用的二者的阻值的比例如何，都是如此。

3 放大器反馈电阻噪声

        反相输入端的噪声贡献包含反馈电阻器的热噪声和运算放大器的电流噪声（受 R1 和 R2 组件的影响）。可以使用基本的运算放大器假设来计算这些噪声源的输出贡献：
• R1 的热噪声电压以电路的反相增益倍数 – R2/R1 放大到输出中
• R2 的热噪声直接贡献到输出噪声中
• 反相输入电流噪声流过 R2，从而带来了IN ×R2 的输出噪声
        这些噪声源是不相关的，因此它们以平方和根值的形式“相加”。但是，可以通过一种更直观的方法来考虑它。将多个噪声源等效为一个在通向输入端的噪声源输入是非常便利的。输出噪声贡献将除以同相增益。
        利用该输入相关 (RTI) 方法，可以轻松地将噪声源与输入信号进行比较。
        在反相输入端发生的噪声与 R1 和 R2 的并联组合相关。当涉及到同相输入时，R1 和 R2 的组合 RTI 热噪声等于 R1//R2 的热噪声。反相输入端的电流噪声 RTI 等于 IN ×(R1//R2)。可见，这些噪声量都取决于R1/R2。

图6

        R1 和 R2 的噪声贡献和反相电流噪声：

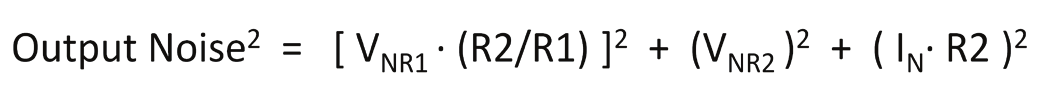
        除以同相增益以得到输入：

        该结果揭示了低噪声涉及的一个重要因素。使 R1//R2 < RS ，这样反相输入端的噪声贡献可以忽略。如果 R1//R2 = RS ，那么反馈网络贡献的噪声与电源电阻的噪声相等。这样的噪声量对于一些特定的设计而言可能显得过多了。
        在高增益中，可以轻松地将并联电阻保持在较低的值 – 可以使R1远小于 Rs，而 R2较大。然而在中等增益时，同样的操作会变得更加困难。当R1和R2相等时，G=2，这是极其糟糕的情
况。例如，如果您使并联电阻为 100Ω，那么R1和R2需要为200Ω。
        那么，反馈网络将会在运放上施加400 Ω的负载，而在大多数情况下，这样的负载值是非常低的。当R1较大而R2较小时，很容易再次接近 G = 1。这种情况并不常见，因为您通常需要在第一个低噪声级实现很高的增益。
        为了解决常见的问题：在使 R2 具有高电阻值时，不存在固有的噪声恶化情况。如果可以通过增大 R2 和减小 R1 同时保持恒定的并联电阻来实现更高的增益，那么噪声性能会保持恒定。

3 1/f 闪烁噪声

        放大器的1/f低频噪声区域似乎有些神秘。它也称为闪烁噪声，就像闪烁的烛光。在示波器上使用慢扫描进行观察时，可以看到它有一条漂移的基线（图 7），因为高频噪声叠加在较大的低频成分上。另一个隐喻名称粉色噪声也暗示了较强的低频分量，闪烁噪声始终存在于在物理系统和生命科学中。

图7

        闪烁噪声的频谱具有 -10 dB/十倍频的标称斜率，这是单极点系统（RC极点）的一半。请注意，电压的平方（或功率）以 1/f 的斜率下降。噪声电压以 1/sqrt(f) 的斜率下降。实际的斜率可能稍微有些变化，但是这并不会较大地改变其行为或结论。
        0.1Hz 噪声成分的周期为 10 秒，因此，要对低至 0.1Hz 的频率进行很好的测量，需要求许多 10 秒周期的平均值 – 这可能会花上五分钟甚至更长的时间。而对于0.01Hz的噪声成分，这样一段长时间的测量时间甚至足够我们去享受一顿悠长的午餐了。另外，这些数据在不同的测量中很可能会得到不同的值。噪声很嘈杂，1/f 噪声似乎比大多数其他噪声更加繁琐。

        为了计算 某个带宽（f1到f2）上的总噪声VB ，对1/f函数求积分，这将得到频率比 f2/f1的自然对数。

va 是 fa 频率下的闪烁点噪声密度。
需要考虑的要点：

• 每十倍频（或其他恒定的频率比）对总噪声具有相同的贡献。每个相继的十倍频具有更低的噪声频率，但具有更大的带宽
• 通过频谱图，可能推断出，当以越来越长的周期进行测量时，1/f 噪声会无限增长。的确是这样，但非常缓慢。0.1 到10Hz 噪声是 3.17e-8Hz 较低带宽（周期为一年）的两倍（大约）。10 年后会增加额外的 6%
• 过滤 1/f 噪声具有挑战性，但并非不可能。0.1Hz 到 1 kHz（四十倍频）的闪烁噪声过滤到 10Hz（二十倍频）仅仅减少了3dB 的噪声。低频噪声的电阻器值必须很小，从而使电阻器具有较大的值，以得到截止频率下限

        放大器噪声由1/f 噪声和白噪声组成。白噪声继续存在于低频率，但 1/f 噪声起主导作用（图 8）。1/f 噪声继续存在于高频率，但白噪声起主导作用。这两种噪声在转角频率处混合，它们随
机相加，使得噪声增加 3dB。在 f1到f2带宽上，分别在该带宽上对1/f 噪声和白噪声求积分，然后以平方和根值的形式进行组合，即得到放大器噪声。
需要考虑的其他要点：

• 闪烁噪声密度增加 N 倍时，转角频率增加 N 2 倍
• 尽管 1/f 噪声区域“看起来较大”，但是从转角频率的下一个十倍频到上一个十倍频的总噪声中白噪声起主导作用 (68%)。

        具有双极结型晶体管 (BJT) 输入级的放大器 (OPA211) 通常具有较低的 1/f 噪声，但新一代模拟集成电路 (IC) 工艺已经极大地改进了结型 FET (JFET) 和互补金属氧化物半导体 (CMOS) 晶体管的闪烁噪声。例如，OPA140 (JFET) 和 OPA376 (CMOS) 运算放大器分别具有 10Hz 和 50Hz 的转角频率。斩波放大器通过校正失调电压变化几乎消除了1/f 噪声。

图8 

4 斩波运放

        斩波运放可提供很低的失调电压，可以极大地降低低频1/f（闪烁）噪声。它们是如何做到的？

        图 9 显示了斩波运算放大器的输入级。该放大器是相对传统的跨导级，具有差分输入和差分输出电流。斩波是在输入和输出的换向开关上完成的，它们同步地反转极性。由于差分输入和输出同时反向，因此输出电容C1上的最终极性是恒定的单向极性。

图9 

        跨导级的失调电压位于输入开关网络内部，因此它对输出的贡献会由输出开关定期反向。失调电压导致的输出电流会导致 C1 上的电压以相同的速率上升和下降。内部逻辑可确保相等的上升和下降时间，因此 C1 上的平均输出电压为零。因此，失调电压为零！早代斩波器仅提供不大的三角斩波滤波，从而导致它们被贴上极度嘈杂的器件的标签，仅用于极低的失调电压至关重要的场合。尤其麻烦的是，预斩波失调电压决定了三角波形的幅度，因此斩波噪声在单元之间可能差异很大。
        新一代斩波器的噪声要小得多，其中包含一个开关电容器滤波器，该滤波器具有多个与斩波频率及其奇次谐波对齐的陷波。这是通过对 C1 上的电荷求一个完整周期的积分，然后将其电荷传输到运算放大器的下一级来实现的。在一个完整的上/下周期上进行积分之后，其净值为零 – 完全平均。在频域中，这将生成一个 sinc(x)或 sin(x)/x 滤波器响应，其零位与三角波的基波和所有谐波准确对齐（图 10）。

        在其最终实现中，输出换向网络中的八个开关交替对两个 C1 电容器进行充电。这可以实现对一个电容器上输入信号的积分，同时另一个电容器上的电荷传输到运算放大器的下一级。
        由于 1/f（闪烁）噪声仅是缓慢的时变失调电压，因此斩波器几乎可以在低频范围内消除该增加的噪声频谱密度。斩波将基带信号移至斩波频率，超出输入级的 1/f 区域。因此，斩波器低频信号范围的噪声频谱密度等于放大器高频范围的噪声频谱密度。
        失调电压为零... 太完美了！当然，仍然存在一些由开关电荷注入以及电容和寄生效应不匹配而产生的残余失调电压误差。输入级增益极大地降低了后续运算放大器级贡献的失调电压。一般而言，较宽的放大器带宽需要较快的斩波，这会增加残余失调电压误差。残余失调电压往往在整个产品生命周期内针对温度非常稳定，这是这些器件的一个重要属性。
        现代斩波运算放大器已经完全取代了标准运放，事实上，完全没有。但是，新一代斩波器确实在更广泛的应用范围中发挥着它们的作用。它们提供极低且稳定的失调电压，几乎没有闪烁噪声，具有非常类似标准运算放大器的表现。

图10