贝叶斯滤波器

最新推荐文章于 2024-06-04 22:20:41 发布

原创最新推荐文章于 2024-06-04 22:20:41 发布 · 661 阅读

0 ·

CC 4.0 BY-SA版权

本文深入探讨了隐马尔科夫模型的核心原理，包括序列组合、联合似然函数、贝叶斯计量求解、时间与测量更新，以及算法流程。通过数学公式详细解析了模型如何基于观测序列进行状态估计，适用于信号处理、语音识别等领域。

1、给定的序列组合

当前状态 $x_n$ 仅取决于最近的过去的状态 $x_{n-1}$ ,通过状态过度分布 $p(x_n|x_{n-1})$ ,初始态 $x_0$ 是分布式的，根据
$p(x_0|y_0)=p(x_0)$

2、联合似然函数

观测值 $y_1,y_2,...,y_n$ 仅条件依赖于相应的状态 $x_1,x_2,...,x_n$ ；这一假设意味着观测值的条件联合似然函数如下：
$l(y1,y2,...,yn∣x1,x2,...,xn)=∏i=1nl(yi∣xi)l(y_1,y_2,...,y_n|x_1,x_2,...,x_n)=\prod _{i=1}^n l(y_i|x_i)$
后验分布 $p(x_n|y_n)$ 在贝叶斯分析至关重要，包含在n时刻，已经接收整个观测序列 $Y_n$ 的条件下，关于 $x_n$ 的全部知识。包含了所有状态估计的必要信息。

3、根据贝叶斯计量求解

例如希望决定状态 $x_n$ 满足最小均方误差时的最优滤波估计，需要解：
$x^n∣n=Ep[xn∣yn]=∫xnp(xn∣Yn)dxn\hat x_{n|n}=E_p[x_n|y_n]=\int x_np(x_n|Y_n)dx_n$
为了滤波估计 $x^n∣n−1\hat x_{n|n-1}$ 精度的评估，计算协方差矩阵：
$Pn∣n=Ep[(xn−x^n∣n)(xn−x^n∣n)T]=∫(xn−x^n∣n)(xn−x^n∣n)Tp(xn∣Yn)dxnP_{n|n}=E_p[(x_n-\hat x_{n|n})(x_n-\hat x_{n|n})^T]=\int (x_n-\hat x_{n|n})(x_n-\hat x_{n|n})^Tp(x_n|Y_n)dx_n$
4、总结
4.1 时间更新
给定观测序列 $Y_{n-1}$ ，计算 $x_n$ 的预测分布，如下所示：
$p(xn∣Yn−1=∫p(xn∣xn−1)p(xn−1∣Yn−1)dxn−1p(x_n|Y_{n-1}=\int p(x_n|x_{n-1})p(x_{n-1|Y_{n-1}})dx_{n-1}$
4.2 测量更新
$p(xn∣Yn)=1Znp(xn∣Yn−1)l(yn∣xn)p(x_n|Y_n)=\frac{1}{Z_n}p(x_n|Y_{n-1})l(y_n|x_n)$
其中
$Zn=p(yn∣yn−1)=∫l(yn∣xn)p(xn∣Yn−1)dxnZ_n=p(y_n|y_{n-1})=\int l(y_n|x_n)p(x_n|Y_{n-1})dx_n$
5 算法框图
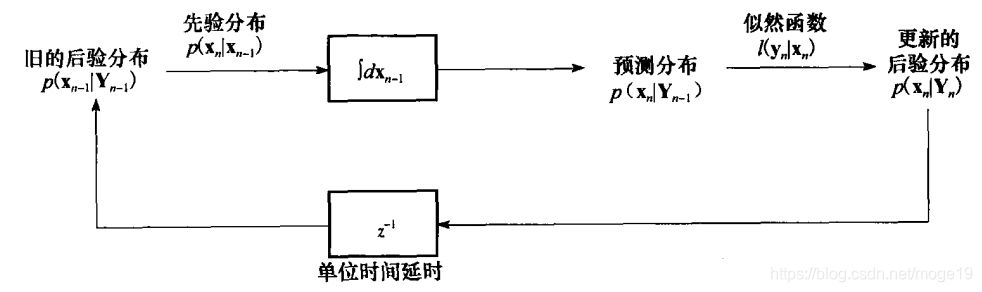
在这里插入图片描述