论文笔记《Accelerating Primal Solution Findings for Mixed Integer Programs Based on Solution Prediction》

1. 引言

1.1 背景

1. 疫情期间，面对收到影响的运输网络，如何规划路由与车线，利用有限的货车资源尽快将积压的包裹运达目的地，这是物流领域典型的组合优化问题，该问题可建模为混合整数规划问题 (Mixed Integer Programing, MIP)，并利用求解器进行求解。
2. 问题：
   （1）快递网络规划问题通常规模很大，包含决策变量和约束条件众多，求解耗时，很难在短时间内求解完成并应用到线上。
   （2）快递网络每天在运转，相似的组合优化问题也需要反复求解，当前尚无处理相似MIP问题的通用方法，每天计算时通常将其视为全新的求解任务

因此，如果能从历史求解中，采用机器学习的方法学习到类似MIP问题的结构特点，则有望大幅提高求解效率。

1.2 文献综述

本文的文献综述主要从两个角度阐述：

1. 将ML(Machine Learning) 和OR(Operations Research，运筹学) 集成以解决CO(combinatorial optimization，组合优化) 问题的研究情况
2. 将ML应用到MLP中，以提高MLP(Mixed Integer Programming，混合整数规划) 效果的研究情况

1.3 创新点

基于上述文献综述，引出本文不同于以往工作的两个方面：

1. 以往研究解决CO问题的方法，都是基于特定的问题结构。本文提出的框架不限于特定的问题类型，而是可以应用到绝大多数的可以用MLP建模的CO问题，即适用范围更大。
2. 以往研究为提高MLP求解效果，均采用人工特征，并且独立对每个变量进行预测。然而实际上，变量的解与目标函数、约束密切相关，因此我们提出三分图(a tripartite graph) 以表征MIP问题，在不需要人工介入的情况下，基于 graph embedding technique 以提取变量、约束、目标函数之间的相关性。

2. 求解框架

2.1 生成训练数据

针对组合优化问题，产生 $p$ 个MIP实例 I = { I 1 , . . . , I p } \mathbb{I}=\left \{I_1,...,I_p\right \} I={ I1​,...,Ip​}，每个 $I_i$ 都存有变量特征、约束特征、边界特征，利用迭代近邻搜索方法(the iterated proximity search method)计算每个 $I_i$ 中的二元变量的label。

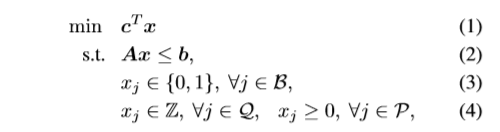
决策变量的索引集 U : = { 1 , . . . , n } \mathcal{U}:=\left \{1,...,n\right \} U:={ 1,...,n} ，被分割成$(\mathcal{B},\mathcal{Q},\mathcal{P})$ ，其中：

• $\mathcal{B}$：二进制变量
• $\mathcal{Q}$：一般整数变量
• $\mathcal{P}$：连续变量

这样做的目的是预测 最优情况下 二元变量 $x_i,j\in \mathcal{B}$ 取值为1或0的概率。

2.2 GCN模型

针对每个 $I_i$ 根据其MIP公式，产生一个三分图。基于已知的特征、label、三分图，训练GCN网络，以求得二元变量预测值。

2.2.1 产生三分图

三分图 $\mathcal{G}=$