论文笔记《Spatial-Temporal Synchronous Graph Convolutional Networks》

最新推荐文章于 2025-10-02 15:59:01 发布
原创 最新推荐文章于 2025-10-02 15:59:01 发布 · 7.2k 阅读 · 71 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

目录

Chao Song, Youfang Lin, Shengnan Guo, Huaiyu Wan*. Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal Network Data Forecasting. Proc. of the 34th AAAI Conference on Artificial Intelligence (AAAI), 2020. (CCF A)

回顾下前面的这篇文章 论文笔记《Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting》
在这里插入图片描述
在这篇文章中存在一个问题，即模型中的时空图卷积块(GCN+Conv 部分) 先在空间维度图卷积，再在时间维度一维卷积，这样的分步操作并没有实现时空相关性的同步捕获。所以，本篇文章重点解决这个问题。

1. Introduction

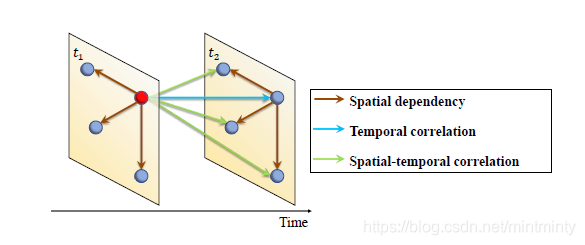
在这里插入图片描述
首先，需要明确在时空网络中的节点的三类依赖关系。之所以会存在这三类依赖关系，是因为时空网络的信息分别在时间和空间维度同时传递。

  • 在同一时间片中，邻居节点与特定点的依赖关系（棕色箭头）
  • 在不同时间片中，特定点对其自身的依赖关系（蓝色箭头）
  • 在不同时间片中，邻居节点对特定点的依赖关系（绿色箭头）

其次，明确现有模型存在的问题。

  • 多数模型都只直接捕获了前两种依赖关系，然后通过将空间表征喂入到针对时间维度建模的模块中，以捕获第三种依赖关系，并不是同时捕获的。
  • 时空网络数据通常在时间维/空间维具有异质性，例如在城市路网中，居住区和商业区在不同时刻常具有不同观测特征，但是以往的模型针对不同时间 共享模型结构，这样一来不能很好地捕获异质性。

最后，明确本文思路。

  • 构造了局部时空图，它将相邻时间步长的单个空间图连接成一个图。
  • 设计Spatial-Temporal Synchronous Graph Convolutional Module (STSGCM) 模块，用以提取局部时空图的时空相关性。
  • 设计Spatial-Temporal Synchronous Graph Convolutional Layer (STSGCL) 层，即在不同时间段部署多个STSGCM，用以捕获长程时空网络数据的异质性。
  • 堆叠多个STSGCL 以聚合长程时空关系和异质性，并得到最终预测结果。

2. Spatial-Temporal Synchronous Graph Convolutional Network

2.1 Localized Spatial-Temporal Graph Construction

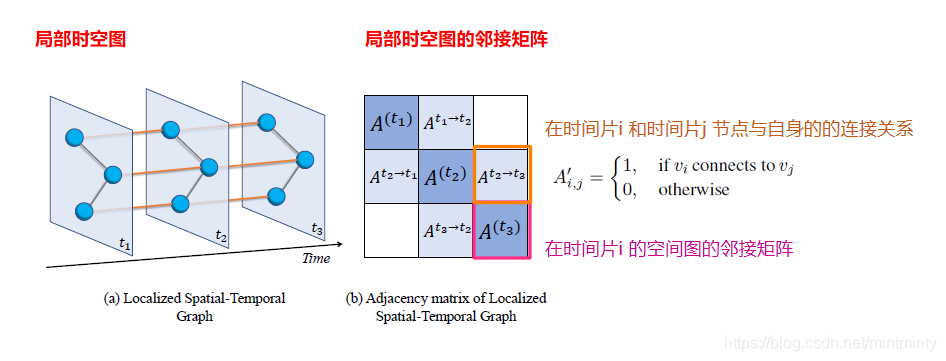
在这里插入图片描述

  • 每个时间片的时空网络图都会有一个局部空间图，这个局部空间图是由连续3个时间片组成。
  • 每个时间片的某节点，不仅有当下时间片的邻居节点，还有前后两个时间片的与自身的邻接关系。
  • 形成的局部时空图表示节点的属性，不随时间变化而变化。

注：这个局部时空图是为后续的图卷积操作服务的，目的是体现各个节点与其多阶邻居的关系，每个节点既有与其同时间步的邻居，还有前后两个时间步的自身节点，还有前后两个时间步自身节点的邻居节点（二阶邻居）。

2.2 Spatial-Temporal Embedding

当将不同时间步的节点放到同一个局部时空图中，就模糊了节点在时空维度的属性。因此，为解决该问题，作者在时空网络序列中添加位置嵌入信息。

  • 对于每个时空网络序列 X g ∈ R N × C × T X_g \in \mathbb{R}^{N\times C\times T} Xg​∈RN×C×T，加一个可学习的时间嵌入矩阵 T e m b ∈ R C × T T_{emb} \in \mathbb{R}^{C\times T} Temb​∈RC×T 和空间嵌入矩阵 S e m b ∈ R N × T S_{emb} \in \mathbb{R}^{N\times T} Semb​∈RN×T，通过广播机制将两个嵌入矩阵添加到时空网络序列中，得到新的网络序列表示
  • 这两个嵌入矩阵是作为参数学习得到的，训练结束后，这两个嵌入矩阵将包含时间和空间信息，从而帮助模型捕获时空相关性
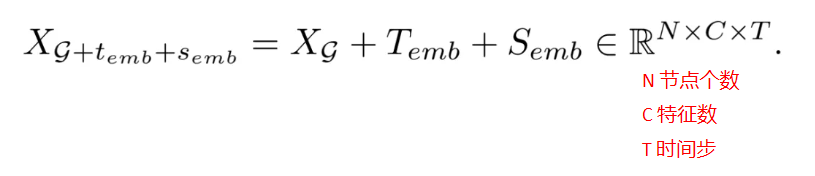
    在这里插入图片描述

注：为什么要进行这步操作呢，是因为刚刚的局部时空图，把三个时间片节点的关系都压到一个矩阵中了，这样一来图卷积网络就会把节点看作是等价的，时空信息被盖掉了，所以要加个时空嵌入表示的方法区分节点。

2.3 Spatial-Temporal Synchronous Graph Convolutional Module

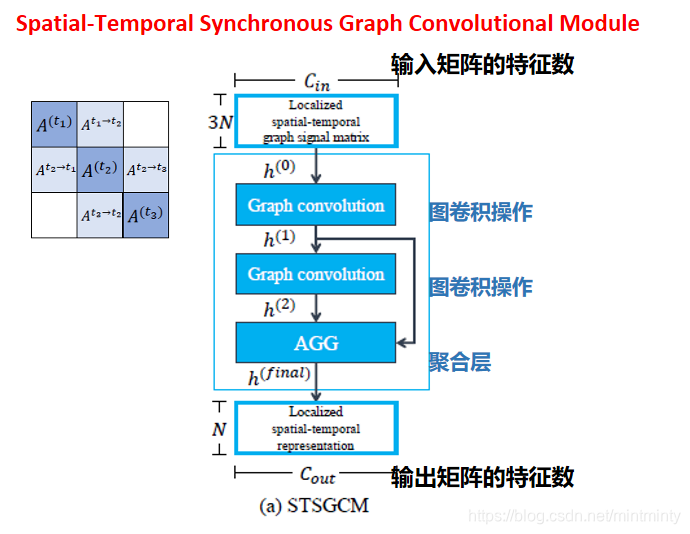
在这里插入图片描述

  • 输入数据为局部时空图的邻接矩阵
  • 接着输入至图卷积层中，进行图卷积操作（基于空域的）
  • 最后进入聚合层(AGG)，聚合层的实现分两步走：聚合(aggregating)和裁剪(cropping)。

Aggregating operation 聚合操作

  • 聚合(aggregating)： 使用最大池化 h A G G = max ⁡ ( h ( 1 ) , h ( 2 ) , … , h ( L ) ) ∈ R 3 N × C o u t h_{A G G}=\max \left(h^{(1)}, h^{(2)}, \ldots, h^{(L)}\right) \in \mathbb{R}^{3 N \times C_{o u t}} hAGG​=max(h(1),h(2),…,h(L))∈R3N
最低0.47元/天 解锁文章
论文笔记--GMAN: A Graph Multi-Attention Network for Traffic Prediction
chenxino的博客
09-17 4026
Chuanpan Zheng, Xiaoliang Fan, Cheng Wang, Jianzhong Qi Summary 在交通预测问题上，作者针对时空因素提出了一种图多注意网络(GMAN)来预测道路网络图上不同位置的时间步长提前的交通状况。GMAN主要采用了编码解码的架构。编码器和解码器之间包含一个注意力转换模块，模拟历史时间步与未来时间步之间的关系，有助于缓解预测时间步之间的误差传播问题。在实验中对与长时间间隔的预测有非常好的效果。 Problem Definition 长时间段的交通
【阅读文献笔记】Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting
qq_46460379的博客
05-25 1056
本文提出了一种新颖的基于注意力机制的空间-时间图卷积网络（ASTGCN）模型，用于交通流量预测。ASTGCN主要由三个独立的组件构成，分别用于建模交通流量的三种时间特性，即近期、日周期和周周期依赖性。每个组件包含两个主要部分：空间-时间注意力机制和空间-时间卷积。空间-时间注意力机制能够有效捕捉交通数据的动态空间-时间相关性；空间-时间卷积则同时利用图卷积捕捉空间模式和标准卷积描述时间特征。三个组件的输出通过加权融合生成最终预测结果。
PEMS-开源
07-09
PEMS 是一个系统，它允许使用超过 RAM 大小的超大数据集执行类似 BSP 的算法（实现为 MPI 程序）。
加州高速路网PeMS交通流量数据集PEMS03
05-10
加州高速路网PeMS交通流量数据集PEMS03。
交通流数据集：PeMs数据集详解与处理方法(包含数据集链接)
最新发布
cccccsp_的博客
10-02 2444
本文将原始的PEMS交通流数据集，转化为可直接用于深度学习模型训练的规范化格式的全过程。我们的旅程始于对数据的探索与可视化，以理解其包含的流量、速度、占有率等多维时序特征，以及传感器节点构成的空间网络结构。在此基础上，我们依次完成了关键的数据预处理步骤：通过线性插值修复了数据中的缺失值，并基于训练集对各个特征进行了标准化。针对数据的空间维度，我们利用传感器间的物理距离，通过高斯核函数与对称归一化技术，精心构建了能够反映路网拓扑关系的图邻接矩阵。而在时间维度上，我们采用滑窗法将切片为大量的监督学习样本。
Spatial-Temporal Synchronous Graph Convolutional Networks: A New
qq_41451283的博客
10-21 448
1.文章概述 当前的一些方法使用不同的模块对不同关系进行建模，本文作者为了同时提取时空关系提出了一个新的模型STSGCN，该模型通过设计了一个时空同步建模机制 和 对不同时间周期设置不同模块分别捕捉时空依赖性和异构性（不同时间阶段有不同的依赖性）。 作者认为在时空预测任务中存在三种关系：空间依赖性，时间依赖性，时空依赖性。当前大部分方法通过同模块捕捉前两种依赖性，第三种依赖性在网络中间接捕捉，作者认为如果可以直接同时捕捉时空依赖对数据的预测非常有效。此外作者认为时空网络数据通常在空间和时间维度上都表现出异
Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal N...
小蚂蚁与大象
06-05 1232
Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal N... 时空网络数据预测在交通管理和城市规划的大量应用中具有重要意义。然而，潜在的复杂时空相关性和异质性使这个问题具有挑战性。现有的方法通常使用单独的分量来获取时空相关性，而忽略了时空数据的异质性。本文提出一种用于时空网络数据预测的新模型——时空同步图卷积网络(STSGCN)。该模型通过精心设计的时空同步建模机制，
论文笔记--Spatial-Temporal Fusion Graph Neural Networks for Traffic Flow Forecasting
chenxino的博客
09-21 1624
Summary 在交通预测问题上，现有的框架通常利用给定的空间邻接图和复杂的机制来建模空间和时间关联。作者认为使用给定的空间邻接图会限制模型的有效时空相关性学习，并且它们通常使用单独的模块来实现空间和时间相关性，或者只使用独立的组件来捕获局部或全局的异质依赖关系，割裂了时空依赖关系。为此作者提出一种时空融合图神经网络用于交通预测。提出一种数据驱动的“时间图”生成方法，以此来补偿空间图可能没有反映的相关性。提出一种新的交通预测方法。 Problem Definition 交通预测中的挑战 以上图为
[论+1]【CAFGCN】Cross-Attention Fusion Based Spatial-Temporal Multi-Graph Convolutional Network for
panbaoran913的博客
06-12 1276
准确的交通流预测对于建设智慧交通城市至关重要。现有的研究主要采用给定的单一图结构作为模型，只考虑局部和静态的空间依赖关系，忽略了动态时空数据多样性的影响。为了充分捕捉时空数据多样性的特点，提出了一种基于交叉注意融合的时空多图卷积网络（CAFMGCN）交通流预测模.....................
GCN在交通流预测方面的相关文章
pixian3729的博客
12-22 2865
文章目录乘客需求量预测（2019ICJAI）STG2Seq: Spatial-Temporal Graph to Sequence Model for Multi-step Passenger Demand Forecasting（2019CIKM）Matrix Factorization for Spatio-Temporal Neural Networks with Applications to Urban Flow Prediction 乘客需求量预测 （2019ICJAI）STG2Seq: Spa
Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal Net
pixian3729的博客
11-09 2139
Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal Network Data Forecasting（时空同步卷积网络） 思想 以前都方法都是单独建立时间空间组件来捕获时空相关性，但是忽略了时空异质性（只是捕获了前两种结构的影响） 时空图中的每个节点都可以在同一时间步直接影响其相邻节点，并且这种影响是从实际的空间依赖性得出的。同时，由于时间序列中的时间相关性，每个节点
Spatial Temporal Graph Convolutional Networks
02-10
时空图卷积网络用于基于骨架的动作识别，Spatial Temporal Graph Convolutional Networks for Skeleton Based Action Recognition，2018年AAAI论文
加州高速路网PeMS交通流量数据集
01-03
加州高速路网PeMS交通流量数据集
加州高速路网PeMS交通流量数据集PEMS07
05-10
加州高速路网PeMS交通流量数据集PEMS07。
PEMS使用说明
11-24
交通领域PEMS数据的使用说明，方便下载PEMS数据，完成交通领域的算法效果验证
【论文解读】Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition
qq_40653311的博客
07-22 4529
论文链接： https://arxiv.org/abs/1801.07455 官方源码： https://github.com/yysijie/st-gcn 1.介绍 当前基于深度学习的动作识别领域主要是对于外观和光流进行建模，而在此之外容易想到的是通过人体骨架。动态骨架模态可以自然地表示为一系列人体关节位置的时间序列，以二维或三维坐标的形式表示，然后通过分析其运动模式，可以识别人类的行为。人体的...
论文1时空同步图卷积网络
qq_43553151的博客
06-27 859
我们将STSGCN的核心思想总结为三点：1.在上一个和下一个时间步骤将每个节点与自己连接起来，以构建一个本地化的时空图。2. 使用时空同步图卷积模块来捕获局部时空相关性。3.部署多个模块对时空网络系列中的异构性进行建模。
解读：时空同步图卷积网络：一种时空网络数据预测的新框架（附项目源码）...
敲代码的quant的博客
12-18 4468
写在前面下面这篇文章的内容主要是来自发表于AAAI 2020的一篇文章《Spatial-Temporal Synchronous Graph Convolutional Network...
【交通数据（1）——加州高速路网PeMS交通数据】
热门推荐
stt666的博客
01-09 4万+
交通数据（1）——加州高速路网PeMS交通数据一、PeMS数据介绍1. 数据简介二、相关数据下载1.引入库2.读入数据 一、PeMS数据介绍 1. 数据简介   使用PeMS，用户可以对高速公路性能进行统一、全面的评估，基于对高速公路网络当前状态的了解做出运营决策，分析拥堵瓶颈以确定潜在的补救措施，并做出更好的整体决策。 是 示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。 二、相关数据下载 1.引入库 PeMS数据官网下载链接 代码如下（示例）： impor
Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting (ASTGCN)
03-19
<think>嗯，用户想了解ASTGCN模型的结构和实现。首先，我得回忆一下这个模型的相关信息。根据引用中的内容，ASTGCN结合了注意力机制和图卷积来处理时空特征。交通数据有时间和空间上的复杂性，所以模型需要同时捕捉这两方面。 模型架构应该分为空间和时间两个部分。空间方面，图卷积网络（GCN）可以处理路网的结构，但交通流量是动态变化的，所以需要注意力机制来调整节点间的关系。引用3提到不同位置的历史数据对未来预测的影响不同，这说明空间注意力是必要的。时间方面，引用4指出过去的交通流会影响未来，所以时间注意力也很重要，用来捕捉不同时间点的重要性。 接下来，模型的具体模块可能包括时空块的堆叠。每个块可能有空间注意力图卷积和时间注意力卷积，再加上门控机制。比如，空间注意力层动态调整邻接矩阵，时间注意力层处理序列中的关键时间点。然后，多组件融合部分可能需要处理不同时间尺度的数据，如最近、日周期、周周期，引用4中的X_h应该对应最近时段的输入。 实现细节方面，图卷积可能用切比雪夫多项式近似，注意力机制通过可学习的参数计算权重。时间卷积可能用一维卷积或LSTM，但结合注意力的话，可能采用自注意力机制。代码示例部分需要展示这些组件的实现，比如定义空间注意力层、时间卷积层，以及如何整合它们。 还要注意引用的内容，比如引用2说明模型在长期预测中的优势，引用5澄清节点特征的组成，每个节点在时间t有F个特征。因此，输入数据的维度应该是N×F×T，其中N是节点数，F是特征数，T是时间步长。 可能还需要考虑如何将多个时空块的输出融合，以及最终的预测层设计。损失函数通常用MAE或RMSE。用户可能需要具体的代码示例，所以需要用PyTorch或TensorFlow框架展示关键层的实现。 最后，相关问题部分要涵盖模型组件的作用、与传统模型的区别、注意力机制的具体应用、数据预处理和实际部署挑战。这能帮助用户更全面地理解ASTGCN的应用和优化方向。</think>### 基于注意力机制的空间-时间图卷积网络（ASTGCN）模型架构及实现 #### 1. 核心设计目标 ASTGCN旨在通过融合图卷积网络（GCN）和注意力机制，捕捉交通数据中的**动态时空关联性**。交通流具有以下特点： - **空间动态性**：路网节点间的关系随时间变化（如早晚高峰拥堵传播）[^3] - **时间动态性**：不同历史时段对预测的影响权重不同（如最近5分钟与1小时前数据的重要性差异）[^4] #### 2. 模型架构 ``` 输入层 → 多组件时空块堆叠 → 融合层 → 输出层 ``` ##### 2.1 空间-时间块（Spatio-Temporal Block） 每个模块包含三层结构： ```python 时空注意力层 → 空间图卷积 → 时间卷积 → 残差连接 ``` - **空间注意力层** 动态计算节点间关联权重矩阵： $$S = \text{softmax}\left( \sigma(\mathbf{X}W_1) \cdot (\mathbf{X}W_2)^T \right)$$ 其中$W_1, W_2$为可学习参数，$\sigma$为激活函数[^2] - **时间注意力层** 计算时间维度权重： $$E = \text{softmax}\left( \text{tanh}(\mathbf{X}U_1) \cdot (\mathbf{X}U_2)^T \right)$$ 通过调整历史时间步的重要性增强时间建模能力 - **门控时序卷积** 使用一维空洞卷积提取多尺度时序特征： ```python class TemporalConv(nn.Module): def __init__(self, in_channels, filters, kernel_size=3): super().__init__() self.conv = nn.Conv1d(in_channels, 2*filters, kernel_size, padding='same') self.tanh = nn.Tanh() self.sigmoid = nn.Sigmoid() def forward(self, x): conv_out = self.conv(x) gate, filter = torch.split(conv_out, split_size, dim=1) return self.tanh(filter) * self.sigmoid(gate) # 门控机制 ``` ##### 2.2 多组件融合 同时处理三种时间模式的数据输入： - **最近时段数据**：$\mathcal{X}_h \in \mathbb{R}^{N \times F \times T_h}$（直接关联当前状态） - **日周期数据**：$\mathcal{X}_d \in \mathbb{R}^{N \times F \times T_d}$（捕捉早晚高峰模式） - **周周期数据**：$\mathcal{X}_w \in \mathbb{R}^{N \times F \times T_w}$（识别工作日/周末差异） #### 3. 关键实现细节 ```python class ASTGCN(nn.Module): def __init__(self, node_num, feat_dim, pred_len): super().__init__() # 空间注意力层 self.spatial_att = SpatialAttention(feat_dim) # 时间卷积层 self.temporal_conv = TemporalConv(feat_dim, 64) # 图卷积层（使用切比雪夫多项式近似） self.gconv = ChebConv(64, 64, K=3) # K为多项式阶数 # 多组件融合 self.fusion = nn.Linear(3*64, pred_len) def forward(self, x_h, x_d, x_w): # 处理最近时段数据 s_att = self.spatial_att(x_h) x_h = F.relu(self.gconv(x_h, s_adj_matrix)) # 动态调整邻接矩阵 x_h = self.temporal_conv(x_h.transpose(1,2)).transpose(1,2) # 类似处理日周期、周周期数据 ... # 特征融合 fused = torch.cat([x_h, x_d, x_w], dim=-1) return self.fusion(fused) ``` #### 4. 模型优势分析 1. **动态空间建模**：通过注意力机制自动学习节点间动态权重，优于传统GCN的固定邻接矩阵 2. **多粒度时间建模**：同时捕捉短期波动和长期周期模式[^4] 3. **并行化处理**：不同时间组件可并行计算提升效率
评论 33
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值