优化问题基本概念

最近在做工程优化项目，接触了全新的概念领域，参考c站各位大神的解答，整理概念笔记如下：

混合整数规划和混合整数二次规划：

https://blog.youkuaiyun.com/wyc648991806/article/details/140738778

二次规划基础知识理论：

最优化 | 二次规划的基础知识理论 | 例题讲解-优快云博客

凸优化问题基础定义：

https://blog.youkuaiyun.com/xu_fengyu/article/details/84727096

原始对偶问题大致介绍：

Primal-Dual原对偶问题大致介绍-优快云博客
原问题、拉格朗日问题、KTT、Slater约束：

优化方法：原问题和拉格朗日对偶问题（primal-dual）_图中标“ ”的点为原问题的最优解x 标“ ”的点为罚函数或增广拉格朗日函数的最优解-优快云博客

原始对偶算法技巧、互补松弛条件：

https://blog.youkuaiyun.com/qx3501332/article/details/105546208

整数规划/混合整数规划+线性规划（原始对偶算法）/二次规划-->（转化为）凸优化问题<—>强对偶性（但不总是成立）：凸优化问题容易求解

凸优化包括线性凸优化和二次凸优化

原问题（函数）：

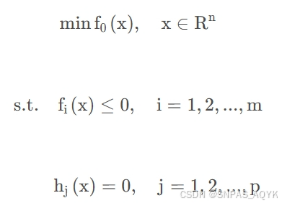
拉格朗日函数：

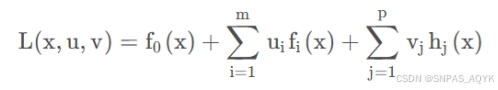
拉格朗日对偶函数：

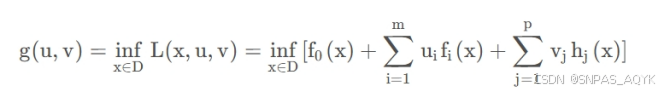
拉氏对偶函数和原函数的关系：

可以用拉格朗日对偶的最大值去逼近原函数的最小值

凸优化问题条件：原函数和不等式约束为凸函数、等式约束为仿射函数

原始对偶方法（Primal-Dual）：思想是从对偶可行解出发, 在满足互补松弛条件的前提下, 使得原始变量朝着可行解的方向迭代。

强对偶性的约束准则：KKT条件和Slater条件
KKT条件：

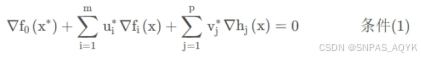
Slater条件：

强对偶性：原问题最优解=拉氏对偶问题最优解

弱对偶性：原问题最优解>=对偶问题最优解，经数学证明总是成立。

对偶间隙（dual gap）：原问题的最优解与拉氏对偶问题的最优解之间的差值。p*表示原问题的最优解，d*表示拉氏对偶函数的最优解。即使当p*和d*无限时，弱对偶性仍然成立。

问题无界：原问题无下界则对偶问题无下界，对偶问题无上界则原问题无上界

仿射函数：仿射函数的标性（值）函数是一次函数f(x)=ax+b，b=0时仿射函数为线性函数

线性规划技术：是多项式时间可解的。通过将整数规划松弛为线性规划后

,得到一个分数解（fractional），之后再将分数解进行取整得到整数规划的整数解。其中primal-dual方法是一种被广泛使用的优化方法，在凸优化和组合优化上有很多应用；其在NP-hard问题的近似算法上也有广泛的使用。