算法导论第8章-线性时间排序

8.1 排序算法的时间下限

比较算法的时间复杂度的下限为nlgn，可用决策树证明该结结论：

假设数组A的长度为n，其中每个元素分别标记为A[1],A[2],A[3]...A[n]，对其进行排序。

对A建立完全二叉树，其中每个节点分别比较A[X]与A[Y]的大小。若A[X]<=A[Y],则走左边，否则走右边

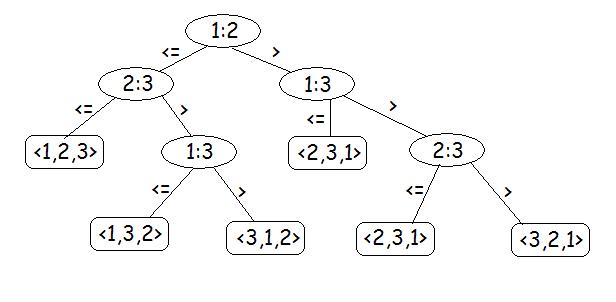
图引自：http://blog.sina.com.cn/s/blog_51cea4040100fd48.html

已知n个节点的全排列个数为n！

比较排序算法能正确的工作，其必要条件是：n个元素的n！种排列中的每一种都要作为决策树的一个叶子节点出现

考虑一颗高度为h，具有l个可达叶节点的决策树，其对应于对n个元素所做的比较排序，有：

由n! <=  l  <=  2^h

=>

h>=nlgn

证毕

8.2 计数排序

基本思想：对每一个输入元素x，确定出小于x的元素个数。有了这一信息就可把x直接放置于其最终输出数组中的合适位置

假设有数组A[8]={2，5，3，0，2，3，0，3}

具体排序步骤如下：

申请数组B和C。

B的大小与A相同，用于存放排序完成后的结果用于输出

C的大小为A的最大值。用于存放数组A中每个数字对应的值

即：

C[0]中存放的是A中小于等于0的数字的个数

C[1]中存放的是A中小于等于1的数字的个数

。。。

C[n]中存放的是A中小于等于n的数字的个数

接下来是关键：

从数字A中的最后一个数字开始：

1.先查询数组中小于等于该数字的个数：C[A[j]

2.将其置入B中相应位置

for(j=length[A] ; j != 0 ; --j)

{

B[C[A[j]]] = A[j];

--C[A[j]] ;

}

之所以循环的j是从length[A]到1递减，是为了保证该算法的稳定性。

令j从1到length[A]递增也能完成排序，但有可能导致算法不稳定

8.3 基数排序

将n位数分为各个位，从低位开始，按某一稳定的排序算法将其排序，最终得到的结果即为最终排序结果

8.4 桶排序

把区间[0,1)划分为n个相同大小的桶，将n个输入均匀分布到各桶中，对每个桶排序，最后按桶顺序输出各个桶，即获得排序效果。

需要注意的是，桶排序要求各数字是均匀分布的，否则桶排序将会退化成普通的排序算法