Codeforces 488B Candy Boxes【思维+分类讨论】

B. Candy Boxes

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There is an old tradition of keeping 4 boxes of candies in the house in Cyberland. The numbers of candies arespecial if theirarithmetic mean, their median and theirrange are all equal. By definition, for a set{x₁, x₂, x₃, x₄} (x₁ ≤ x₂ ≤ x₃ ≤ x₄)arithmetic mean is 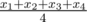,median is 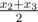andrange isx₄ - x₁.The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.

For example, 1, 1, 3, 3 is the example of 4 numbers meeting the condition because their mean, median and range are all equal to2.

Jeff has 4 special boxes of candies. However, something bad has happened! Some of the boxes could have been lost and now there are onlyn (0 ≤ n ≤ 4) boxes remaining. Thei-th remaining box containsa_i candies.

Now Jeff wants to know: is there a possible way to find the number of candies of the4 - n missing boxes, meeting the condition above (the mean, median and range are equal)?

Input

The first line of input contains an only integer n (0 ≤ n ≤ 4).

The next n lines contain integers a_i, denoting the number of candies in thei-th box (1 ≤ a_i ≤ 500).

Output

In the first output line, print "YES" if a solution exists, or print "NO" if there is no solution.

If a solution exists, you should output 4 - n more lines, each line containing an integerb, denoting the number of candies in a missing box.

All your numbers b must satisfy inequality1 ≤ b ≤ 10⁶. It is guaranteed that if there exists a positive integer solution, you can always find suchb's meeting the condition. If there are multiple answers, you are allowed to print any of them.

Given numbers a_i may follow in any order in the input, not necessary in non-decreasing.

a_i may have stood at any positions in the original set, not necessary on lowestn first positions.

Examples

Input

2
1
1

Output

YES
3
3

Input

3
1
1
1

Output

NO

Input

4
1
2
2
3

Output

YES

Note

For the first sample, the numbers of candies in 4 boxes can be1, 1, 3, 3. The arithmetic mean, the median and the range of them are all2.

For the second sample, it's impossible to find the missing number of candies.

In the third example no box has been lost and numbers satisfy the condition.

You may output b in any order.

题目大意：

给你n个数，如果能找到4-n个数，使得这四个数满足：x1<=x2<=x3<=x4&&(x1+x2+x3+x4)/4==(x2+x3)/2==x4-x1；输出YES，并且输出其他4-n个数，否则输出NO。

思路：

1、首先有：

(x1+x2+x3+x4)/4==(x2+x3)/2------------------->能够推出x2+x3==x1+x4;

(x2+x3)/2==x4-x1-------------->能够推出x2+x3==2x4-2x1

将上述两个式子联立，能够得出：x4=x1*3的结论。

 

2、接下来我们分类讨论：

①n==0，输出任意可行解即可。

②n==1，输出a【1】，a【1】*3，a【1】*3即可（其实也是任意可行解）。

③n==2，首先输入没有保证递增性，那么我们要将这两个数排序，然后设定a【4】=a【1】*3，那么a【3】的值我们可以通过枚举来判定，因为结果输出保证了是1e6内的数据，那么我们枚举一层for，如果有可行解输出即可，如果没有可行解输出NO。

④n==3，直接枚举最后一个数，枚举出来之后，将这四个数排序，并且判断是否是一个可行解，如果是，输出即可。

⑤n==4，直接判断是否是一个可行解即可。

3、细节参考代码、

Ac代码：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int a[15];
int ans[15];
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&a[i]);
        }
        sort(a+1,a+n+1);
        if(n==0)
        {
            printf("YES\n1\n1\n3\n3\n");
        }
        if(n==4)
        {
            if((a[1]+a[2]+a[3]+a[4])/4==(a[2]+a[3])/2&&(a[2]+a[3])/2==a[4]-a[1])
            {
                printf("YES\n");
            }
            else printf("NO\n");
        }
        if(n==1)
        {
            printf("YES\n");
            printf("%d\n%d\n%d\n",a[1],a[1]*3,a[1]*3);
        }
        if(n==2)
        {
            a[4]=a[1]*3;
            int flag=0;
            for(int i=1; i<=1000000; i++)
            {
                a[3]=i;
                if((a[1]+a[2]+a[3]+a[4])/4==(a[2]+a[3])/2&&(a[2]+a[3])/2==a[4]-a[1])
                {
                    flag=1;
                    printf("YES\n");
                    break;
                }
            }
            if(flag==0)printf("NO\n");
            else
            {
                printf("%d\n%d\n",a[3],a[4]);
            }
        }
        if(n==3)
        {
            int flag=0;
            for(int i=1; i<=1000000; i++)
            {
                a[4]=i;
                int tmp[5];
                tmp[1]=a[1];
                tmp[2]=a[2];
                tmp[3]=a[3];
                tmp[4]=a[4];
                sort(tmp+1,tmp+5);
                if(tmp[1]*3!=tmp[4])continue;
                if((tmp[1]+tmp[2]+tmp[3]+tmp[4])/4==(tmp[2]+tmp[3])/2&&(tmp[2]+tmp[3])/2==tmp[4]-tmp[1])
                {
                    flag=1;
                    printf("YES\n%d\n",i);
                    break;
                }
            }
            if(flag==0)printf("NO\n");
        }
    }
}