Moore vs. Mealy Machine

slides from https://inst.eecs.berkeley.edu/~cs150/fa05/Lectures/07-SeqLogicIIIx2.pdf

[GPT 3.5]

A Mealy machine can have fewer states than a Moore machine because in a Mealy machine, the output depends on both the current state and the input, whereas in a Moore machine, the output depends only on the current state. This means that in a Mealy machine, states can be merged if they produce the same output for the same input, even if they transition to different states. In a Moore machine, states cannot be merged if they produce the same output, but transition to different states.

Here's an example to illustrate this:

Let's say we want to design a machine that detects a sequence of two consecutive 1's in a binary input. We can implement this using both a Mealy machine and a Moore machine.

**Mealy machine:**

In this Mealy machine, the state `q3` outputs a 1 when the input is 1, indicating that the sequence `11` has been detected. The output of `q3` depends on both the current state and the input. However, `q2` and `q3` produce the same output for input 0, so we can merge them into a single state.

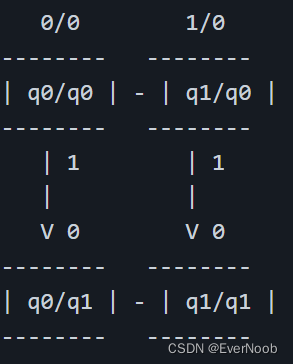
**Moore machine:**

In this Moore machine, the state `q1/q0` outputs a 1 when the sequence `11` has been detected. The output of `q1/q0` depends only on the current state, not the input. However, we cannot merge `q0/q0` and `q0/q1` because they produce different outputs.

As we can see, the Mealy machine has fewer states than the Moore machine because we were able to merge `q2` and `q3` in the Mealy machine, but we couldn't do so in the Moore machine.

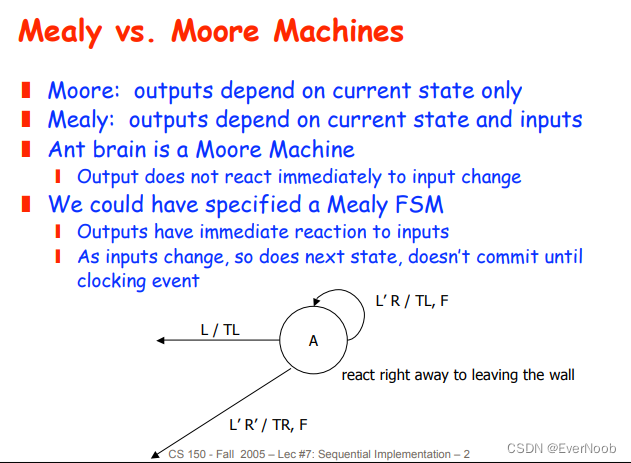
==> output is not dependent on input, but next state still is

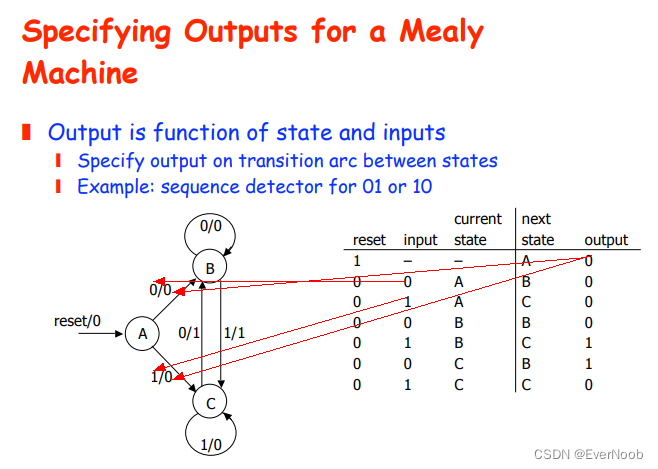
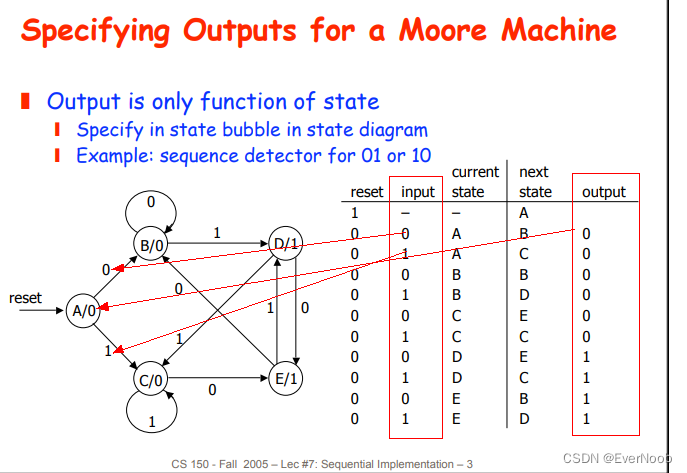
with the merging rule stated in the beginning:

(starting from the Moore diagram, but change it to a Mealy first, then)

E is merged into B

D is merged into C

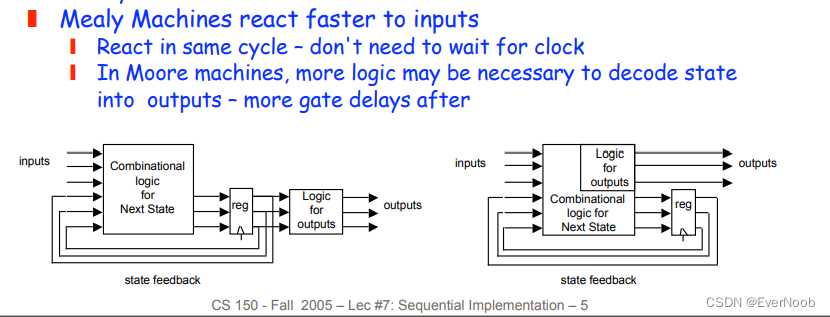
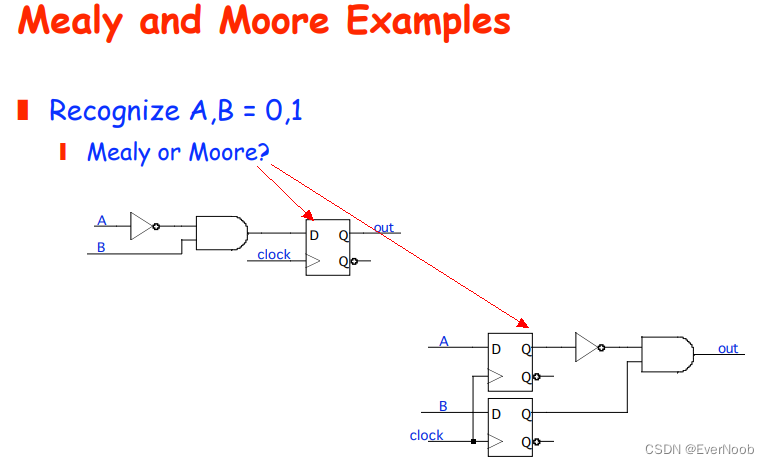
both outputs are dependent on states only

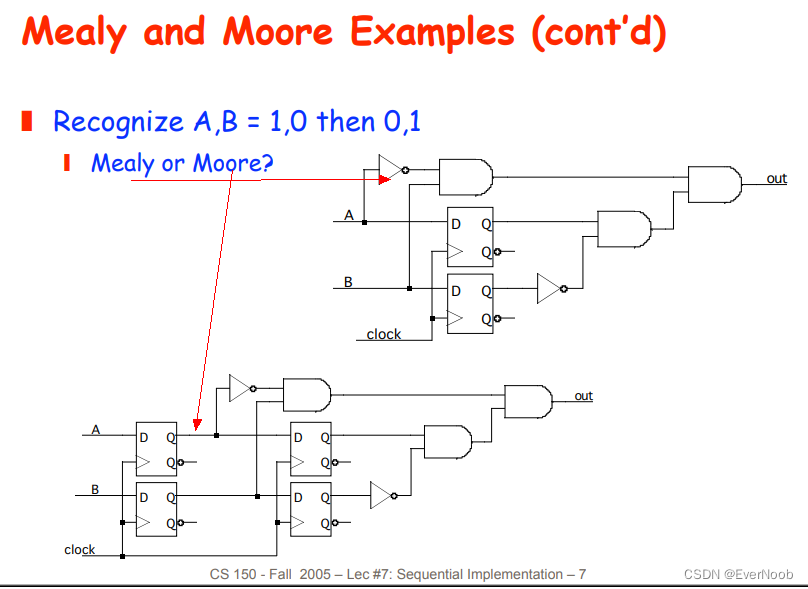
use registered Mealy to improve output safety

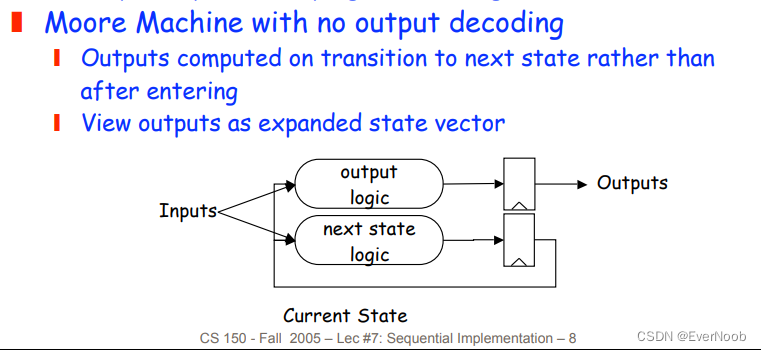
which makes it Moore Machine, without a decoder for output

see the slides for extended examples.