剑指offer05矩形覆盖

题目描述
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2n的大矩形，总共有多少种方法？
比如n=3时，23的矩形块有3种覆盖方法：

思路：
一开始又蒙圈了，看到长方形又是长又是宽觉得有些乱，虽然提示是递归但是就不知道该怎么用了。
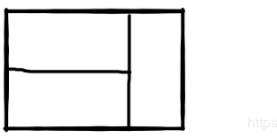
仔细思考需要覆盖的目标长方形的宽是2，第一个放的长方形如果是竖着放相当于目标长方形宽不变如下图左图所示，长-1，第一个放的长方形如果横着放，则为了覆盖下边必须再横放一个长方形如右图所示，这时目标长方形宽不变，长-2。综上，目标长方形的长就可以理解为跳台阶的台阶数，长每次减1或减2，和跳台阶完全一样的题目，如果宽不是2的话这道题该怎么做咧

代码同03 04题

# -*- coding:utf-8 -*-
class Solution:
    def rectCover(self, number):
        # write code here
        res = 0
        if (number == 1):
            res = 1
        elif (number == 2):
            res = 2
        else:
            res = self.rectCover(number-1)+self.rectCover(number-2)*2
        return res

修改为

# -*- coding:utf-8 -*-
class Solution:
    def rectCover(self, number):
        # write code here
        res = 0
        ppnum = 1
        pnum = 2
        if (number == 1):
            res = 1
        elif (number == 2):
            res = 2
        else:
            for i in range(3,number+1):
                res = pnum+ppnum
                ppnum = pnum
                pnum = res
        return res