分类预测 | MATLAB实现KOA-CNN-BiLSTM开普勒算法优化卷积双向长短期记忆神经网络数据分类预测

✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎 往期回顾关注个人主页：Matlab科研工作室

🍊个人信条：格物致知,完整Matlab代码获取及仿真咨询内容私信。

🔥 内容介绍

在数据分类领域，面对时序与空间特征耦合的复杂数据（如传感器监测数据、金融时序数据、生物信号数据），传统卷积神经网络（CNN）虽擅长提取空间局部特征，但难以捕捉长时序依赖；双向长短期记忆神经网络（BiLSTM）虽能建模前后向时序关系，却存在初始参数随机化导致的收敛慢、易陷入局部最优等问题。基于此，本文提出开普勒算法优化卷积双向长短期记忆神经网络（KOA-CNN-BiLSTM），通过开普勒算法（Kepler Optimization Algorithm, KOA）对 CNN-BiLSTM 的关键超参数进行全局寻优，提升网络的特征提取能力与分类预测精度，为复杂数据分类任务提供高效解决方案。

一、KOA-CNN-BiLSTM 模型核心构成：从算法到网络的融合逻辑

1. 核心组件基础特性

（1）开普勒算法（KOA）：超参数优化的 “全局搜索工具”

KOA 是 2022 年提出的新型元启发式优化算法，模拟天体在开普勒定律约束下的运动规律（椭圆轨道运行、万有引力作用），核心优势在于全局搜索能力强、收敛速度快、参数依赖性低，适用于神经网络超参数的高维复杂空间寻优：

• 搜索机制：

• 将待优化超参数（如 CNN 卷积核数量、BiLSTM 隐藏层节点数）编码为 “天体”，每个天体的位置对应一组超参数组合；

• 通过 “椭圆轨道更新” 模拟全局搜索（基于万有引力公式计算天体间的引力作用，引导天体向最优位置移动），通过 “局部扰动” 实现局部精细搜索（避免陷入局部最优）；

• 目标函数：以 CNN-BiLSTM 在验证集上的分类准确率为适应度函数，目标是寻找使适应度值最大的超参数组合。

（2）卷积神经网络（CNN）：空间特征提取的 “核心模块”

CNN 通过 “卷积层 - 池化层” 的堆叠结构，实现对数据空间局部特征的自动提取，尤其适用于含空间关联的多维数据（如多通道传感器数据的局部异常特征、图像数据的纹理特征）：

• 卷积层：通过可学习的卷积核对输入数据进行滑动卷积，捕捉局部特征（如 3×3 卷积核提取数据的局部梯度变化）；

• 池化层：通过最大池化或平均池化降低特征维度，减少计算量的同时增强网络对数据微小变形的鲁棒性；

• 输出层：通过全连接层将卷积提取的高维特征映射为低维特征向量，为后续 BiLSTM 的时序建模提供输入。

（3）双向长短期记忆神经网络（BiLSTM）：时序依赖建模的 “关键模块”

BiLSTM 由 “前向 LSTM” 与 “后向 LSTM” 组成，可同时捕捉数据的前向时序依赖（如前一时刻传感器数据对当前时刻的影响）与后向时序依赖（如后一时刻数据对当前时刻的反馈），解决传统 LSTM 单向建模的局限性：

• LSTM 单元：通过输入门、遗忘门、输出门的门控机制，有效缓解长时序数据的梯度消失问题，实现长序列记忆；

• 双向融合：将前向 LSTM 与后向 LSTM 的输出特征拼接，形成包含完整时序信息的特征向量，提升对时序数据上下文关系的建模能力；

• 分类层：通过 Softmax 激活函数将 BiLSTM 输出的时序特征映射为各类别的概率分布，实现数据分类预测。

2. KOA-CNN-BiLSTM 融合架构与工作流程

（1）模型整体架构

KOA-CNN-BiLSTM 采用 “KOA 超参数优化 + CNN-BiLSTM 特征提取与分类” 的两阶段架构：

1. 超参数优化阶段：通过 KOA 在超参数搜索空间内寻找最优组合；

1. 分类预测阶段：基于最优超参数构建 CNN-BiLSTM 模型，完成数据的 “空间特征提取 - 时序依赖建模 - 分类预测”。

（2）完整工作流程

1. 数据预处理：

• 对输入数据进行标准化（如 Z-score 标准化）、时序截断（将长时序数据切分为固定长度的样本）、标签编码（如 One-Hot 编码），构建训练集、验证集、测试集；

1. KOA 超参数寻优：

• 超参数定义：确定待优化超参数及搜索范围（如 CNN 卷积核数量 [16,64]、卷积核大小 [3,5]、BiLSTM 隐藏层节点数 [32,128]、学习率 [0.001,0.01]、批大小 [16,64]）；

• KOA 初始化：设置 KOA 的种群规模（如 30）、最大迭代次数（如 50），随机生成初始超参数种群；

• 适应度计算：对每个超参数组合，构建对应的 CNN-BiLSTM 模型，在训练集上训练并计算验证集分类准确率（适应度值）；

• 种群更新：基于开普勒定律更新天体位置（超参数组合），重复适应度计算与种群更新，直至迭代结束，输出最优超参数组合；

1. CNN-BiLSTM 分类预测：

• 模型构建：基于最优超参数搭建 CNN-BiLSTM 模型（如 CNN 含 2 个卷积层 + 1 个池化层，BiLSTM 含 1 个双向隐藏层，分类层采用 Softmax）；

• 模型训练：在训练集上采用交叉熵损失函数与 Adam 优化器训练模型，通过早停（Early Stopping）防止过拟合；

• 分类预测：将测试集输入训练好的模型，输出各类别概率，以最大概率对应的类别作为最终分类结果；

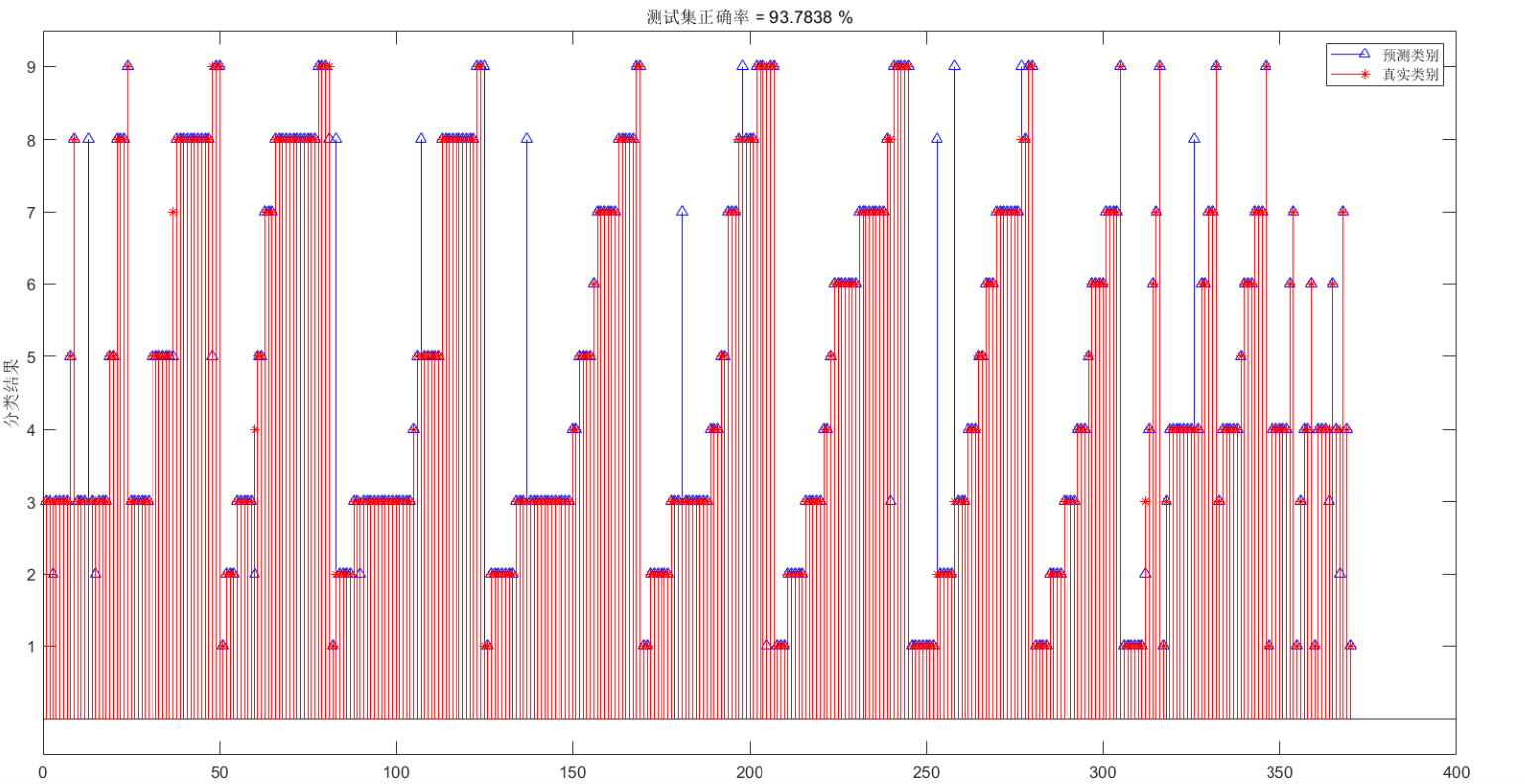
1. 性能评估：采用分类准确率、精确率、召回率、F1 分数、混淆矩阵等指标评估模型分类性能。

⛳️ 运行结果

📣 部分代码

%开普勒优化算法

function [Sun_Score,Sun_Pos,Convergence_curve]=KOA(SearchAgents_no,Tmax,lb,ub,dim,feval)

%%%%-------------------Definitions--------------------------%%

%%

Sun_Pos=zeros(1,dim); % A vector to include the best-so-far Solution, representing the Sun

Sun_Score=inf; % A Scalar variable to include the best-so-far score

Convergence_curve=zeros(1,Tmax);

if length(lb)==1

lb = lb*ones(1,dim);

ub = ub*ones(1,dim);

end

%%-------------------Controlling parameters--------------------------%%

%%

Tc=3;

M0=0.1;

lambda=15;

%% Step 1: Initialization process

%%---------------Initialization----------------------%%

% Orbital Eccentricity (e)

orbital=rand(1,SearchAgents_no); %% Eq.(4)

%% Orbital Period (T)

T=abs(randn(1,SearchAgents_no)); %% Eq.(5)

Positions=initialization(SearchAgents_no,dim,ub,lb); % Initialize the positions of planets

t=0; %% Function evaluation counter

%%

%%---------------------Evaluation-----------------------%%

for i=1:SearchAgents_no

%% Test suites of CEC-2014, CEC-2017, CEC-2020, and CEC-2022

PL_Fit(i)=feval( Positions(i,:));

% Update the best-so-far solution

if PL_Fit(i)<Sun_Score % Change this to > for maximization problem

Sun_Score=PL_Fit(i); % Update the best-so-far score

Sun_Pos=Positions(i,:); % Update te best-so-far solution

end

end

while t<Tmax %% Termination condition

[Order] = sort(PL_Fit); % Sorting the fitness values of the solutions in current population

%% The worst Fitness value at function evaluation t

worstFitness = Order(SearchAgents_no); %% Eq.(11)

M=M0*(exp(-lambda*(t/Tmax))); %% Eq. (12)

%% Computer R that represents the Euclidian distance between the best-so-far solution and the ith solution

for i=1:SearchAgents_no

R(i)=0;

for j=1:dim

R(i)=R(i)+(Sun_Pos(j)-Positions(i,j))^2; %% Eq.(7)

end

R(i)=sqrt(R(i));

end

%% The mass of the Sun and object i at time t is computed as follows:

for i=1:SearchAgents_no

sum=0;

for k=1:SearchAgents_no

sum=sum+(PL_Fit(k)-worstFitness);

end

MS(i)=rand*(Sun_Score-worstFitness)/(sum); %% Eq.(8)

m(i)=(PL_Fit(i)-worstFitness)/(sum); %% Eq.(9)

end

%% Step 2: Defining the gravitational force (F)

% Computing the attraction force of the Sun and the ith planet according to the universal law of gravitation:

for i=1:SearchAgents_no

Rnorm(i)=(R(i)-min(R))/(max(R)-min(R)); %% The normalized R (Eq.(24))

MSnorm(i)=(MS(i)-min(MS))/(max(MS)-min(MS)); %% The normalized MS

Mnorm(i)=(m(i)-min(m))/(max(m)-min(m)); %% The normalized m

Fg(i)=orbital(i)*M*((MSnorm(i)*Mnorm(i))/(Rnorm(i)*Rnorm(i)+eps))+(rand); %% Eq.(6)

end

%% a1 represents the semimajor axis of the elliptical orbit of object i at time t,

for i=1:SearchAgents_no

a1(i)=rand*(T(i)^2*(M*(MS(i)+m(i))/(4*pi*pi)))^(1/3); %% Eq.(23)

end

for i=1:SearchAgents_no

%% a2 is a cyclic controlling parameter that is decreasing gradually from -1 to ?2

a2=-1+-1*(rem(t,Tmax/Tc)/(Tmax/Tc)); %% Eq.(29)

%% ? is a linearly decreasing factor from 1 to ?2

n=(a2-1)*rand+1; %% Eq.(28)

a=randi(SearchAgents_no); %% An index of a solution selected at random

b=randi(SearchAgents_no); %% An index of a solution selected at random

rd=rand(1,dim); %% A vector generated according to the normal distribution

r=rand; %% r1 is a random number in [0,1]

%% A randomly-assigned binary vector

U1=rd<r; %% Eq.(21)

O_P=Positions(i,:); %% Storing the current position of the ith solution

%% Step 6: Updating distance with the Sun

if rand<rand

%% h is an adaptive factor for controlling the distance between the Sun and the current planet at time t

h=(1/(exp(n.*randn))); %% Eq.(27)

%% An verage vector based on three solutions: the Current solution, best-so-far solution, and randomly-selected solution

Xm=(Positions(b,:)+Sun_Pos+Positions(i,:))/3.0;

Positions(i,:)=Positions(i,:).*U1+(Xm+h.*(Xm-Positions(a,:))).*(1-U1); %% Eq.(26)

else

%% Step 3: Calculating an object? velocity

% A flag to opposite or leave the search direction of the current planet

if rand<0.5 %% Eq.(18)

f=1;

else

f=-1;

end

L=(M*(MS(i)+m(i))*abs((2/(R(i)+eps))-(1/(a1(i)+eps))))^(0.5); %% Eq.(15)

U=rd>rand(1,dim); %% A binary vector

if Rnorm(i)<0.5 %% Eq.(13)

M=(rand.*(1-r)+r); %% Eq.(16)

l=L*M*U; %% Eq.(14)

Mv=(rand*(1-rd)+rd); %% Eq.(20)

l1=L.*Mv.*(1-U);%% Eq.(19)

V(i,:)=l.*(2*rand*Positions(i,:)-Positions(a,:))+l1.*(Positions(b,:)-Positions(a,:))+(1-Rnorm(i))*f*U1.*rand(1,dim).*(ub-lb); %% Eq.(13a)

else

U2=rand>rand; %% Eq. (22)

V(i,:)=rand.*L.*(Positions(a,:)-Positions(i,:))+(1-Rnorm(i))*f*U2*rand(1,dim).*(rand*ub-lb); %% Eq.(13b)

end %% End IF

%% Step 4: Escaping from the local optimum

% Update the flag f to opposite or leave the search direction of the current planet

if rand<0.5 %% Eq.(18)

f=1;

else

f=-1;

end

%% Step 5

Positions(i,:)=((Positions(i,:)+V(i,:).*f)+(Fg(i)+abs(randn))*U.*(Sun_Pos-Positions(i,:))); %% Eq.(25)

end %% End If

%% Return the search agents that exceed the search space's bounds

if rand<rand

for j=1:size(Positions,2)

if Positions(i,j)>ub(j)

Positions(i,j)=lb(j)+rand*(ub(j)-lb(j));

elseif Positions(i,j)<lb(j)

Positions(i,j)=lb(j)+rand*(ub(j)-lb(j));

end %% End If

end %% End For

else

Positions(i,:) = min(max(Positions(i,:),lb),ub);

end %% End If

%% Test suites of CEC-2014, CEC-2017, CEC-2020, and CEC-2022

% Calculate objective function for each search agent

PL_Fit1=feval(Positions(i,:));

% Step 7: Elitism, Eq.(30)

if PL_Fit1<PL_Fit(i) % Change this to > for maximization problem

PL_Fit(i)=PL_Fit1; %

% Update the best-so-far solution

if PL_Fit(i)<Sun_Score % Change this to > for maximization problem

Sun_Score=PL_Fit(i); % Update the best-so-far score

Sun_Pos=Positions(i,:); % Update te best-so-far solution

end

else

Positions(i,:)=O_P;

end %% End IF

t=t+1; %% Increment the current function evaluation

if t>Tmax %% Checking the termination condition

break;

end %% End IF

Convergence_curve(t)=Sun_Score; %% Set the best-so-far fitness value at function evaluation t in the convergence curve

end %% End for i

end %% End while

Convergence_curve(t-1)=Sun_Score;

end%% End Function

🔗 参考文献

🎈 部分理论引用网络文献，若有侵权联系博主删除

 👇 关注我领取海量matlab电子书和数学建模资料 

🏆团队擅长辅导定制多种科研领域MATLAB仿真，助力科研梦：

🌟 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱调度、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化、CVRP问题、VRPPD问题、多中心VRP问题、多层网络的VRP问题、多中心多车型的VRP问题、 动态VRP问题、双层车辆路径规划（2E-VRP）、充电车辆路径规划（EVRP）、油电混合车辆路径规划、混合流水车间问题、 订单拆分调度问题、 公交车的调度排班优化问题、航班摆渡车辆调度问题、选址路径规划问题、港口调度、港口岸桥调度、停机位分配、机场航班调度、泄漏源定位、冷链、时间窗、多车场等、选址优化、港口岸桥调度优化、交通阻抗、重分配、停机位分配、机场航班调度、通信上传下载分配优化

🌟 机器学习和深度学习时序、回归、分类、聚类和降维

2.1 bp时序、回归预测和分类

2.2 ENS声神经网络时序、回归预测和分类

2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类

2.4 CNN|TCN|GCN卷积神经网络系列时序、回归预测和分类

2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类

2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类

2.7 ELMAN递归神经网络时序、回归\预测和分类

2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类

2.9 RBF径向基神经网络时序、回归预测和分类

2.10 DBN深度置信网络时序、回归预测和分类

2.11 FNN模糊神经网络时序、回归预测

2.12 RF随机森林时序、回归预测和分类

2.13 BLS宽度学习时序、回归预测和分类

2.14 PNN脉冲神经网络分类

2.15 模糊小波神经网络预测和分类

2.16 时序、回归预测和分类

2.17 时序、回归预测预测和分类

2.18 XGBOOST集成学习时序、回归预测预测和分类

2.19 Transform各类组合时序、回归预测预测和分类

方向涵盖风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、用电量预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

🌟图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

🌟 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、 充电车辆路径规划（EVRP）、 双层车辆路径规划（2E-VRP）、 油电混合车辆路径规划、 船舶航迹规划、 全路径规划规划、 仓储巡逻、公交车时间调度、水库调度优化、多式联运优化

🌟 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化、车辆协同无人机路径规划、

🌟 通信方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化、水声通信、通信上传下载分配

🌟 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化、心电信号、DOA估计、编码译码、变分模态分解、管道泄漏、滤波器、数字信号处理+传输+分析+去噪、数字信号调制、误码率、信号估计、DTMF、信号检测

🌟电力系统方面

微电网优化、无功优化、配电网重构、储能配置、有序充电、MPPT优化、家庭用电、电/冷/热负荷预测、电力设备故障诊断、电池管理系统（BMS）SOC/SOH估算（粒子滤波/卡尔曼滤波）、 多目标优化在电力系统调度中的应用、光伏MPPT控制算法改进（扰动观察法/电导增量法）、电动汽车充放电优化、微电网日前日内优化、储能优化、家庭用电优化、供应链优化

🌟 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长 金属腐蚀

🌟 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合、SOC估计、阵列优化、NLOS识别

🌟 车间调度

零等待流水车间调度问题NWFSP 、 置换流水车间调度问题PFSP、 混合流水车间调度问题HFSP 、零空闲流水车间调度问题NIFSP、分布式置换流水车间调度问题 DPFSP、阻塞流水车间调度问题BFSP

👇

5 往期回顾扫扫下方二维码