【路径规划】基于固定次序法的移植最短距离路径规划附Matlab代码

 ✅作者简介：热爱数据处理、建模、算法设计的Matlab仿真开发者。

🍎更多Matlab代码及仿真咨询内容点击 🔗：Matlab科研工作室

🍊个人信条：格物致知。

🔥 内容介绍

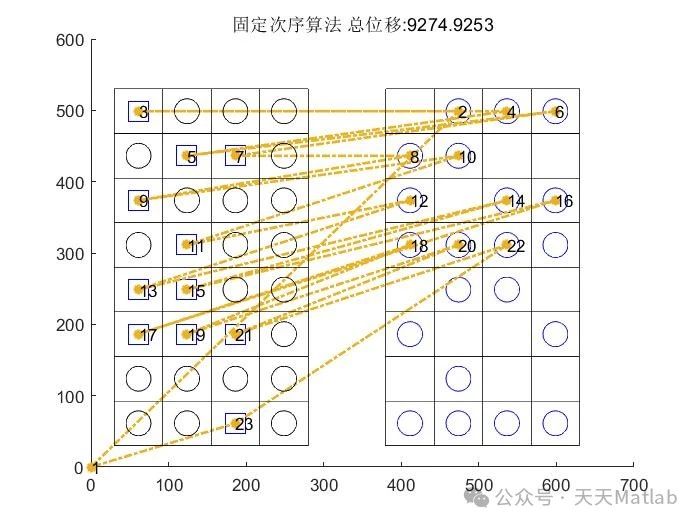
路径规划作为机器人学、人工智能和计算机图形学等领域的关键问题，旨在寻找一条从起点到终点满足特定约束条件的最优路径。本文将探讨一种基于固定次序法的移植最短距离路径规划算法，并结合Matlab代码进行详细阐述，分析其优缺点及适用场景。 固定次序法，顾名思义，是一种预先设定节点访问顺序的路径规划方法。它通过预先定义一个节点访问序列，然后依次搜索，最终连接起点和终点，找到一条满足条件的路径。与其他全局搜索算法（如A*算法、Dijkstra算法）相比，其计算复杂度相对较低，尤其在处理大型地图或实时性要求较高的场景中具有优势。然而，其路径并非全局最优，而是基于预设顺序的局部最优解。

一、算法原理及步骤

基于固定次序法的移植最短距离路径规划算法的核心思想是将地图离散化为一个图，其中每个节点代表地图中的一个位置，边代表节点之间的连接，边的权重表示节点间距离。算法流程如下：

1. 地图表示: 将地图离散化为一个图 G = (V, E)，其中 V 表示节点集合，E 表示边集合。每个节点 v ∈ V 具有坐标 (x, y)，边 e ∈ E 连接两个节点，并具有权重 w(e)，表示两个节点间的欧几里得距离或曼哈顿距离等。 此步骤通常需要进行地图预处理，例如栅格地图的创建和障碍物的识别。

2. 节点次序确定: 预先定义一个节点访问顺序 π = (v1, v2, ..., vn)，其中 vi ∈ V。 这个顺序可以根据不同的策略确定，例如：

   • 随机顺序: 随机排列所有节点。

   • 启发式顺序: 根据节点与起点或终点的距离进行排序，优先访问距离较近的节点。

   • 基于领域知识的顺序: 根据对地图的先验知识，设定一个合理的访问顺序。

3. 路径搜索: 按照预设的节点访问顺序 π，依次搜索可达路径。从起点开始，依次访问 π 中的节点，如果节点之间存在连接且未被访问，则将其加入路径。 需要注意的是，该算法不考虑全局最优性，只考虑在当前访问顺序下的局部最优路径。 为了找到更短的路径，可以采用贪心策略，选择距离当前节点最近且未访问的节点加入路径。

4. 路径连接: 如果最终访问到了终点，则算法结束，得到一条从起点到终点的路径。如果无法到达终点，则可能需要重新确定节点访问顺序或调整算法参数。

5. 路径优化 (可选): 获得初始路径后，可以进一步优化路径，例如，通过局部搜索算法，消除路径中的冗余部分，以得到更短、更平滑的路径。

二、Matlab 代码实现

以下代码展示了基于固定次序法的移植最短距离路径规划的Matlab实现，假设地图已表示为邻接矩阵的形式。

if adjMatrix(currentNode, nextNode) ~= inf
path = [path, nextNode];
currentNode = nextNode;
end
end

% 判断是否到达终点
if currentNode == endNode
disp('路径已找到:');
disp(path);
else
disp('无法到达终点!');
end

% 计算路径长度
pathLength = 0;
for i = 1:length(path)-1
pathLength = pathLength + adjMatrix(path(i), path(i+1));
end
disp(['路径长度: ', num2str(pathLength)]);

这段代码只是一个简单的示例，实际应用中需要根据具体地图和需求进行修改和完善，例如加入障碍物检测、路径平滑处理等功能。 更复杂的场景可能需要更高级的数据结构和算法来处理大型地图和复杂的约束条件。

三、算法优缺点及适用场景

优点:

• 计算复杂度低: 相对于全局搜索算法，固定次序法计算复杂度较低，尤其在处理大型地图时具有优势。

• 易于实现: 算法实现简单，易于理解和维护。

• 适合实时应用: 由于计算速度快，该算法适合于对实时性要求较高的场景。

缺点:

• 路径非全局最优: 算法仅搜索基于预设顺序的局部最优路径，无法保证找到全局最短路径。

• 对节点顺序敏感: 路径结果严重依赖于节点访问顺序的选择，不同的顺序可能导致路径长度差异很大。

• 难以处理复杂约束: 对于具有复杂约束条件的路径规划问题，该算法的适用性较差。

适用场景:

• 实时性要求高的场景: 例如机器人导航、自动驾驶等，需要快速找到一条可行的路径，即使不是最优路径。

• 地图信息不完整或不精确的场景: 在某些情况下，地图信息可能不完整或不精确，此时固定次序法可以作为一种快速获得近似解的方法。

• 预先设定路径顺序的场景: 例如，在一些特定应用场景中，可能需要按照预定的顺序访问某些节点，此时固定次序法非常适用。

四、总结与展望

本文介绍了一种基于固定次序法的移植最短距离路径规划算法，并提供了Matlab代码实现。 该算法计算效率高，易于实现，适用于一些实时性要求高或地图信息不完整的场景。 然而，其路径并非全局最优，且对节点顺序敏感。 未来的研究可以关注如何改进节点顺序的确定策略，结合启发式算法或机器学习方法，提高路径规划的效率和路径质量。 此外，可以探索将该算法与其他路径规划算法结合，以发挥各自优势，解决更复杂的路径规划问题。 例如，可以将固定次序法作为预处理步骤，生成一个初始路径，然后利用其他全局优化算法对其进行改进。

⛳️ 运行结果

🔗 参考文献

🎈 部分理论引用网络文献，若有侵权联系博主删除