✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,
代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
特征提取是数字信号处理中的重要步骤,它可以帮助我们从原始数据中提取出有用的信息,为后续的分析和处理提供基础。在音频信号处理中,基音频率是一个重要的特征,它可以帮助我们识别音频中的基本音调和音高变化。本文将介绍基于自相关函数(ACF)和加权平均幅度差函数(W-AMDF)的基音频率计算方法。
ACF是一种常用的信号处理工具,它可以帮助我们找出信号中的周期性成分。在音频信号处理中,ACF可以用来计算信号的基音频率。基音频率是指音频信号中最低的频率成分,它对应着音调的基本频率。通过计算音频信号的ACF,我们可以找出信号中的周期性成分,从而推断出基音频率。
另一种常用的基音频率计算方法是W-AMDF。W-AMDF在计算基音频率时考虑了信号的幅度变化,因此可以更准确地找出基音频率。W-AMDF首先计算出信号的幅度差函数,然后对其进行加权平均,最后找出幅度差函数的最小值对应的位置,即为基音频率的估计值。
在实际的音频信号处理中,我们可以结合ACF和W-AMDF的方法来计算基音频率。首先使用ACF方法对音频信号进行基音频率的初步估计,然后再利用W-AMDF方法进行精细化的计算。这样可以充分发挥两种方法的优势,得到更准确的基音频率估计结果。
总之,基音频率是音频信号中的重要特征之一,它可以帮助我们理解音频中的音调和音高变化。通过基于ACF和W-AMDF的基音频率计算方法,我们可以更准确地提取出音频信号中的基音频率信息,为后续的音频处理和分析提供可靠的基础。希望本文对大家在音频信号处理中的特征提取工作有所帮助。
📣 部分代码
clear all; clc; close all;filedir=[]; % 设置路径filename='s.wav'; % 设置文件名fle=[filedir filename]; % 构成完整的路径和文件名[xx,Fs]=audioread(fle); % 读入数据文件x=detrend(xx); % 消除直流分量wlen=200; inc=80; % 设置帧长、帧移win=hanning(wlen); % 窗函数N=length(x); % 求数据长度X=enframe(x,win,inc)'; % 分帧fn=size(X,2); % 获取帧数zcr1=zeros(1,fn); % 初始化for i=1:fnz=X(:,i); % 取得一帧数据for j=1: (wlen-1); % 在一帧内寻找过零点if z(j)* z(j+1)< 0 % 判断是否为过零点zcr1(i)=zcr1(i)+1; % 是过零点,记录1次endendendtime=(0:N-1)/Fs; % 计算时间坐标frameTime=frame2time(fn,wlen,inc,Fs); % 求出每帧对应的时间% 作图subplot 211; plot(time,x,'k'); grid;title('语音波形');ylabel('幅值'); xlabel(['时间/s' 10 '(a)']);subplot 212; plot(frameTime,zcr1,'k'); grid;title('短时平均过零率');ylabel('幅值'); xlabel(['时间/s' 10 '(b)']);
⛳️ 运行结果
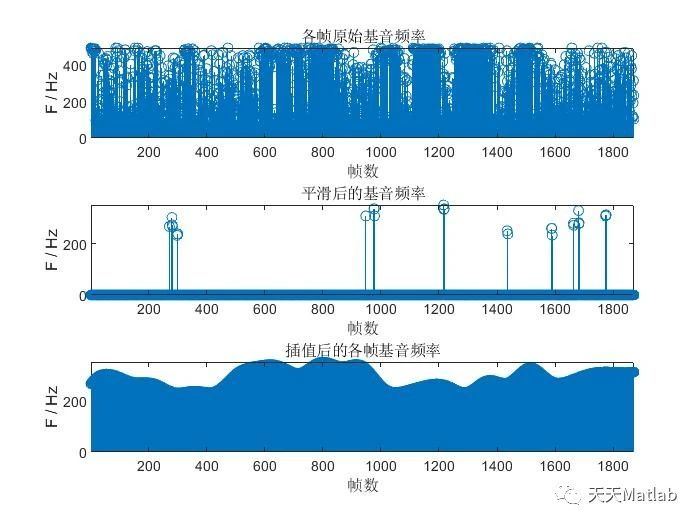
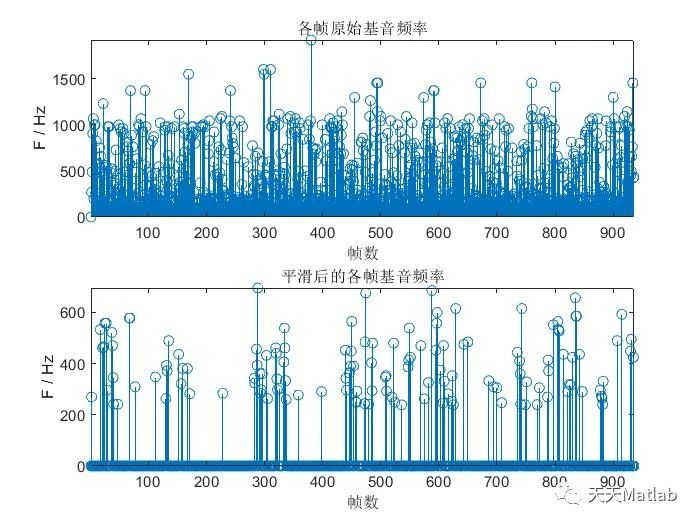





 本文介绍了如何在音频信号处理中使用自相关函数(ACF)和加权平均幅度差函数(W-AMDF)计算基音频率,这两种方法有助于提取音频的音调和音高信息。Matlab示例代码展示了如何在实际应用中进行基音频率的计算。
本文介绍了如何在音频信号处理中使用自相关函数(ACF)和加权平均幅度差函数(W-AMDF)计算基音频率,这两种方法有助于提取音频的音调和音高信息。Matlab示例代码展示了如何在实际应用中进行基音频率的计算。

















 963
963

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










