✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
在现代制造业中,车间调度是一个至关重要的环节。通过合理安排车间内各个工序的顺序和时间,可以提高生产效率,减少生产成本,提升产品质量。而随着自动化技术的发展,自动导引车(Automated Guided Vehicles,简称AGV)在车间调度中起到了越来越重要的作用。本文将介绍一种基于樽海鞘算法的车间调度方法,用于解决带小车的车间调度AGV-fjsp问题。
AGV-fjsp问题是指在车间调度中,需要考虑到AGV和作业工序之间的关系。在传统的车间调度中,通常只需要考虑作业工序之间的先后次序。而在AGV-fjsp问题中,还需要考虑到AGV与作业工序之间的时间和空间关系,以及AGV之间的冲突避免。这使得AGV-fjsp问题更加复杂,需要使用更加高效的算法来求解。
樽海鞘算法是一种基于自然界中樽海鞘行为的启发式算法。樽海鞘是一种生物,它们通过释放化学物质来吸引其他樽海鞘,形成聚集。这种聚集行为可以用来解决优化问题。樽海鞘算法通过模拟樽海鞘的聚集行为,来求解复杂的优化问题。
在车间调度AGV-fjsp问题中,樽海鞘算法可以用来寻找最优的车间调度方案。首先,将车间调度问题抽象为一个优化问题,其中目标是最小化总的调度时间和冲突次数。然后,使用樽海鞘算法来搜索最优解。樽海鞘算法通过模拟樽海鞘的聚集和分散行为,来搜索解空间中的最优解。
具体来说,樽海鞘算法包括以下几个步骤。首先,初始化一群随机生成的樽海鞘个体,每个个体代表一个可能的车间调度方案。然后,根据每个个体的适应度评估,选择一部分个体作为父代。接下来,通过模拟樽海鞘的聚集行为,生成新的个体。然后,根据一定的概率,对新生成的个体进行变异操作,以增加搜索空间。最后,根据适应度评估,选择新生成的个体和父代中的个体,作为下一代的父代。重复以上步骤,直到满足停止准则。
通过使用樽海鞘算法求解车间调度AGV-fjsp问题,可以得到较优的车间调度方案。这种方案可以最大程度地减少总的调度时间和冲突次数,提高车间生产效率。同时,樽海鞘算法具有较好的全局搜索能力,能够避免局部最优解。因此,它在解决车间调度AGV-fjsp问题中具有较高的应用价值。
总之,车间调度是现代制造业中的重要环节,而AGV-fjsp问题则是车间调度中的一种复杂问题。通过使用樽海鞘算法,可以求解带小车的车间调度AGV-fjsp问题,并得到较优的调度方案。这种方法可以提高车间生产效率,降低生产成本,提升产品质量。因此,樽海鞘算法在车间调度AGV-fjsp问题中具有广泛的应用前景。
📣 部分代码
function [so,sm,sv] = heuristic_Population()%% 功能:启发式初始化global AGV_num ps job_number machine_number operations_number operations_vector operations_start_vector feasible_machines_table time_table trans_time_table operations_number_vectorso1=zeros(ps,operations_number);sm1=zeros(ps,operations_number); % 存机器sv1=zeros(ps,operations_number); % 存机器for i=1:ps%% 工序:初始化indices=randperm(operations_number); % 将300以内的数随机排列so1(i,:)=operations_vector(indices); % 得到工件号排序的工序%% 机器:选择完工时间最早的机器ML=zeros(1,machine_number); % 记录全局机器时间TT=zeros(1,machine_number); % 用来临时比较% 生成机器Number=operations_number_vector;WPNumberTemp=Number;for j=1:operations_numberval=so1(i,j);WPNumberTemp(val)=WPNumberTemp(val)-1;temp=[val,operations_number_vector(val)-WPNumberTemp(val)]; % 第一个数表示工件号,第二个数表示工件内对应的工序号op_position=sum(operations_number_vector(1:val-1))+temp(2); % 总工序表中第几个 如O13表示3machines_list = 1:machine_number;Temp1 = machines_list(logical(feasible_machines_table(op_position,:))); % 工序Oij可选机器time1 = time_table(op_position,:); % 例[3 7]time1(find(time1==0))=[];Temp2=time1;Temp=[Temp1;Temp2];SizeTemp=size(Temp,2);%查看该工序有几个可用机器if SizeTemp == 1sm1(i,op_position)=Temp(1,1); % 如果只有一个可选机器,就直接存入ML(Temp(1))=Temp(2,1); % 更新ML表elseif SizeTemp>=2% TT=ML+time 选全局最小机器for ii=1:SizeTempjob=Temp(1,ii); % 取可选机器集内第ii个机器time=Temp(2,ii); % 取对应时间TT(job)=ML(job)+time; % 加入TT时间表用来比较选机器end[~,indice]=min(TT(Temp(1,:)));TT=zeros(1,machine_number); % 清空TT表,以备下一个工序选机器ML(Temp(1,indice))=Temp(2,indice); % 更新MLsm1(i,op_position)=Temp(1,indice);endend%% AGV初始化% AGV_current_machine=zeros(AGV_num,operations_number*2); % 存AGV当前在哪个机器machineoRagV=zeros(AGV_num,machine_number+1); % 用0-1存当前机器是否有AGVmachineoRagV(:,1)=1; % 首先对装卸站位置赋值(所有的AGV初始时刻均在装卸站)job_current_op=ones(1,job_number);for j=1:operations_number% jjob=so1(i,j); operation=job_current_op(1,job);index=operations_start_vector(1,job)+operation; % 该工序索引job_current_op(1,job)=job_current_op(1,job)+1; % 更新当前加工工序if operation==1 % 判断是否是首道工序% sv1(1,index)=randi([1,AGV_num],1,1); % 首道工序随机选择AGV% elseif ismember(1,machineoRagV(:,1)) % 判断起点是否有AGVtempm=sm1(i,index); % 当前工序对应机器编号tempm=tempm+1;startindex=find(machineoRagV(:,1)==1); % 装卸站可用的AGV编号AGV_code=startindex(randi([1 length(startindex)])); % 选择在装卸站的AGVmachineoRagV(AGV_code,1)=0; machineoRagV(AGV_code,tempm)=1; % 更新AGV当前所在的位置sv1(i,index)=AGV_code; % 将选择的AGV的编号放入初始编码中else % 装卸站没有AGVtempm=sm1(i,index); % 当前工序对应机器编号tempm=tempm+1;distance=zeros(1,AGV_num); % 初始距离矩阵agvmac=[];for k=1:AGV_num % 循环所有的AGV% 计算距离nowAgvIndex=find(machineoRagV(k,:)==1); % 当前AGV所在的位置agvmac=[agvmac;nowAgvIndex]; % 存一下agv所在机器distance(1,k)=trans_time_table(nowAgvIndex,1)+trans_time_table(1,tempm);end% 选择距离最小的AGV[~,sv1(i,index)]=min(distance);% 更新一下当前AGV的位置machineoRagV(sv1(i,index),agvmac(sv1(i,index),1))=0; machineoRagV(sv1(i,index),tempm)=1; % 更新AGV当前所在的位置agvmac=[];endelse % 非首道工序,只需要计算与上一个工序所在机器tempm=sm1(i,index); % 当前工序对应机器编号premac=sm1(i,index-1); % 上一个工序所在机器编号premac1=premac+1;tempm=tempm+1;distance=zeros(1,AGV_num); % 初始距离矩阵agvmac=[];for k=1:AGV_num % 循环所有的AGV% 计算距离nowAgvIndex=find(machineoRagV(k,:)==1); % 当前AGV所在的位置% nowAgvIndexagvmac=[agvmac;nowAgvIndex]; % 存一下agv所在机器distance(1,k)=trans_time_table(premac1,tempm)+trans_time_table(nowAgvIndex,premac1);end% 选择距离最小的AGV[~,sv1(i,index)]=min(distance);% 更新一下当前AGV的位置machineoRagV(sv1(i,index),agvmac(sv1(i,index),1))=0; machineoRagV(sv1(i,index),tempm)=1; % 更新AGV当前所在的位置agvmac=[];endendso=so1;sm=sm1;sv=sv1;end
⛳️ 运行结果
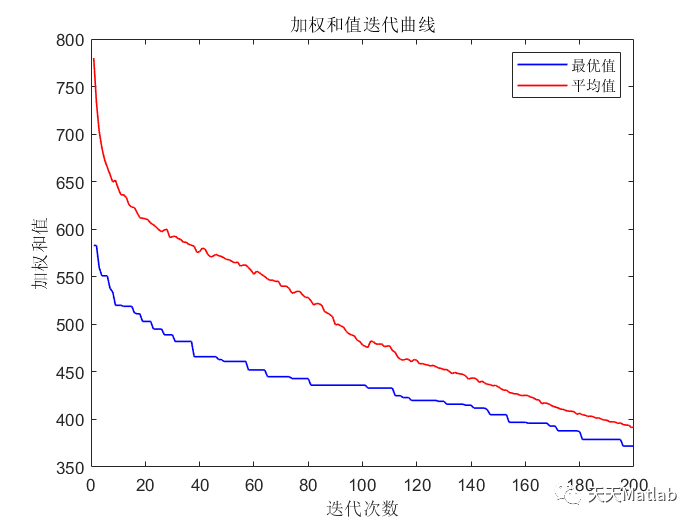
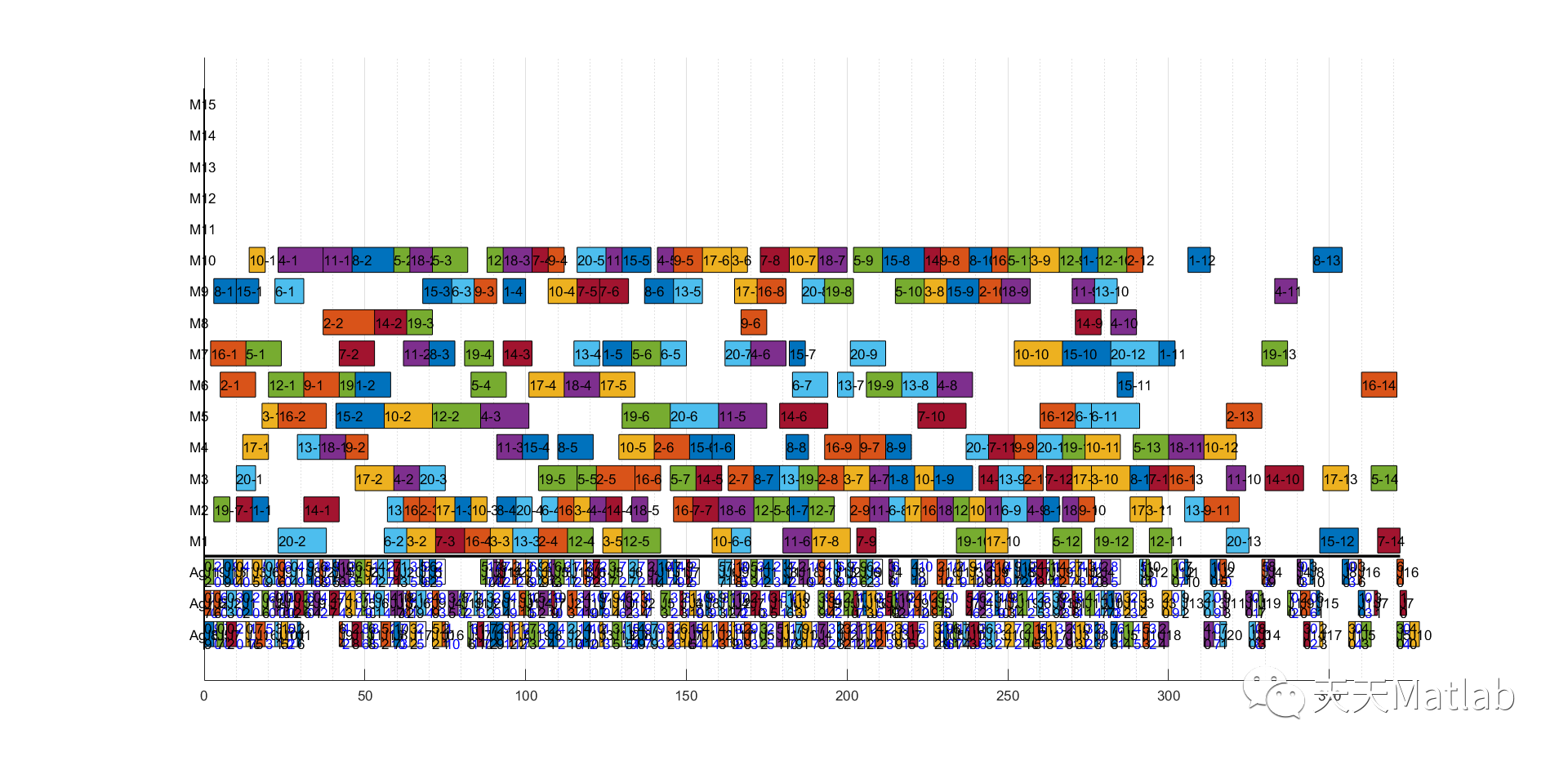
🔗 参考文献
[1] 阎庆,邰蕾蕾.用混合遗传算法解决有时间窗的车辆路径规划问题[J].安徽大学学报:自然科学版, 2007, 31(2):4.DOI:CNKI:SUN:AHDX.0.2007-02-010.
[2] 王原,李晓苗.基于T型传递函数的二进制樽海鞘算法求解0-1背包问题[J].电子技术与软件工程, 2022(011):000.
[3] LI Changan,ZHAO Delong,WANG Guoyong,等.基于改进樽海鞘群算法的卸车调度优化[J].重庆交通大学学报(自然科学版), 2021, 40(11):32-39.DOI:10.3969/j.issn.1674-0696.2021.11.05.
[4] 袁友伟,高一鸣,黄笑成,等.一种基于改进樽海鞘算法的工作流优化调度方法.CN202211260945.8[2023-10-13].





 本文聚焦现代制造业车间调度,介绍基于樽海鞘算法解决带小车的车间调度AGV - fjsp问题。该问题需考虑AGV与作业工序时空关系及AGV冲突避免,樽海鞘算法模拟樽海鞘行为搜索最优解,可减少调度时间和冲突次数,提高车间生产效率。
本文聚焦现代制造业车间调度,介绍基于樽海鞘算法解决带小车的车间调度AGV - fjsp问题。该问题需考虑AGV与作业工序时空关系及AGV冲突避免,樽海鞘算法模拟樽海鞘行为搜索最优解,可减少调度时间和冲突次数,提高车间生产效率。

















 966
966

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










