1 内容介绍
作业车间调度问题一直是国内外学者研究的热点,柔性作业车间调度问题是在经典作业车间调度问题的基础上发展起来的一种更加复杂的组合优化问题,工序的加工机器不再限定在一台机器上,可以在多台机器上加工,加工时间也互不相同,求解难度更大,被称为最坏的NP难问题之一。相对于经典作业车间调度问题,柔性作业车间调度问题更加符合实际加工车间的生产调度情况,于是柔性作业车间调度问题成为近年来学术界和工程技术领域研究的热点。本文的研究就是围绕柔性作业车间调度问题展开的,主要工作如下:根据柔性作业车间调度的基本理论和现行作业车间的实际情况,结合蚁群算法的相关原理,确定本文的研究对象为柔性作业车间静态调度问题,以最大完工时间最小化为优化目标,建立了基于旅行商问题的作业车间调度问题析取图模型,选择用帝国企鹅算法求解。
2 仿真代码
function [fit,result]=aimFcn_1(x,option,data)
global option data
x=reshape(x,data.numP,data.numM);
MT=zeros(1,data.numM); %每个机器当前工作结束的时间
PT=zeros(1,data.numP); %每个工序被完成的时间
flag=zeros(1,data.numP); %每个工序是否被完成
PJ=ones(1,data.numJ); %每个工件的当前工序
recording=[];
while sum(flag)~=data.numP
%查找当前可开工的工序编号
for noJ=1:data.numJ
noP=PJ(noJ);
position=find(data.Process(:,1)==noJ & data.Process(:,2)==noP);
if isempty(position)
tempMT(noJ,:)=inf;
tempPri(noJ,:)=inf;
tempPri1(noJ,:)=inf;
tempPri2(noJ,:)=inf;
else
tempMT(noJ,:)=data.Process(position,3:end);
tempPri(noJ,:)=x(position,:);
tempPri1(noJ,:)=data.lambda_gama(position,2:end);
tempPri2(noJ,:)=repmat(data.lambda_gama(position,1),1,data.numM);
end
tempST(noJ,:)=MT+1;
end
temp=tempMT.*tempPri.*tempST./tempPri1./tempPri2;
[p1,p2]=find(temp==min(min(temp)));
noJ=p1(1);
noM=p2(1);
noP=PJ(noJ);
position=find(data.Process(:,1)==noJ & data.Process(:,2)==noP);
if noP==1
ST=0;
else
position1=find(data.Process(:,1)==noJ & data.Process(:,2)==noP-1);
ST=PT(position1);
end
ST=max(ST,MT(noM));
T=data.Process(position,2+noM);
MT(noM)=ST+T;
PJ(noJ)=PJ(noJ)+1;
flag(position)=1;
PT(position)=ST+T;
lambda=data.Process(position,1);
gama=data.Process(position,1+noM);
recording=[recording;noJ,noP,noM,ST,T,ST+T,lambda,gama];
end
fit=-data.Z*sum(recording(:,7).*recording(:,8)./recording(:,5));
if nargout>1
result.fit=-fit;
result.recording=recording;
end
end
%% 这是使用原始算法的直接求解结果,添加专用于本问题的更新方式可以进一步提高精度
% This is the direct result of using the original algorithm,
% adding some specific update methods to this problem can further improve the accuracy
clc;
clear;
close all;
warning off
%% 固定随机数种子
noRNG=1;
rng('default')
rng(noRNG)
%% 载入数据
data.Process=xlsread('data.xlsx',1);
data.lambda_gama=xlsread('data.xlsx',2);
data.numP=length(data.Process(:,1));
data.numJ=max(data.Process(:,1));
data.numM=4; %机器数量
data.Z=10;
dim=data.numP*data.numM;
%%
option.dim=dim; %八个决策变量
lb=0;
ub=1;
option.lb=lb;
option.ub=ub;
if length(option.lb)==1
option.lb=ones(1,option.dim)*option.lb;
option.ub=ones(1,option.dim)*option.ub;
end
option.fobj=@aimFcn_1;
%option.fobj0=option.fobj;
option.showIter=0;
%% 算法参数设置 Parameters
% 基本参数
option.numAgent=20; %种群个体数 size of population
option.maxIteration=20; %最大迭代次数 maximum number of interation
% 帝企鹅算法
option.v_lb=-(option.ub-option.lb)/4;
option.v_ub=(option.ub-option.lb)/4;
option.w2=0.5; %weight of Moving strategy III
option.w4=1;%weight of Moving strategy III
option.w5=1;%weight of Moving strategy III
option.pe=0.01; % rate to judge Premature convergence
option.gap0=ceil(sqrt(option.maxIteration*2))+1;
option.gapMin=5; % min gap
option.dec=2; % dec of gap
option.L=10; % Catastrophe
str_legend=[{'AFO1'},{'AFO2'}];
%% Initialize population individuals (common to control experiment algorithm)
x=ones(option.numAgent,option.dim);
y=ones(option.numAgent,1);
for i=1:option.numAgent
x(i,:)=rand(size(option.lb)).*(option.ub-option.lb)+option.lb;
y(i)=option.fobj(x(i,:),option,data);
end
%% 使用算法求解
% Based on the same population, solve the selected functions by using different algorithms
bestX=x;
rng(noRNG)
tic
[bestY(1,:),bestX(1,:),recording(1)]=AFO1(x,y,option,data);
tt(1,1)=toc;
rng(noRNG)
tic
[bestY(2,:),bestX(2,:),recording(2)]=AFO2(x,y,option,data);
tt(1,2)=toc;
%%
figure
hold on
for i=1:length(recording)
plot(-(recording(i).bestFit),'LineWidth',2)
end
legend(str_legend)
title('fitness curve')
%% 输出结果
str='AFO1'
[~,result1]=option.fobj(bestX(1,:),option,data);
color=colormap(jet);
drawPC(result1,color,str)
str='AFO2'
[~,result2]=option.fobj(bestX(2,:),option,data);
color=colormap(jet);
drawPC(result2,color,str)
3 运行结果
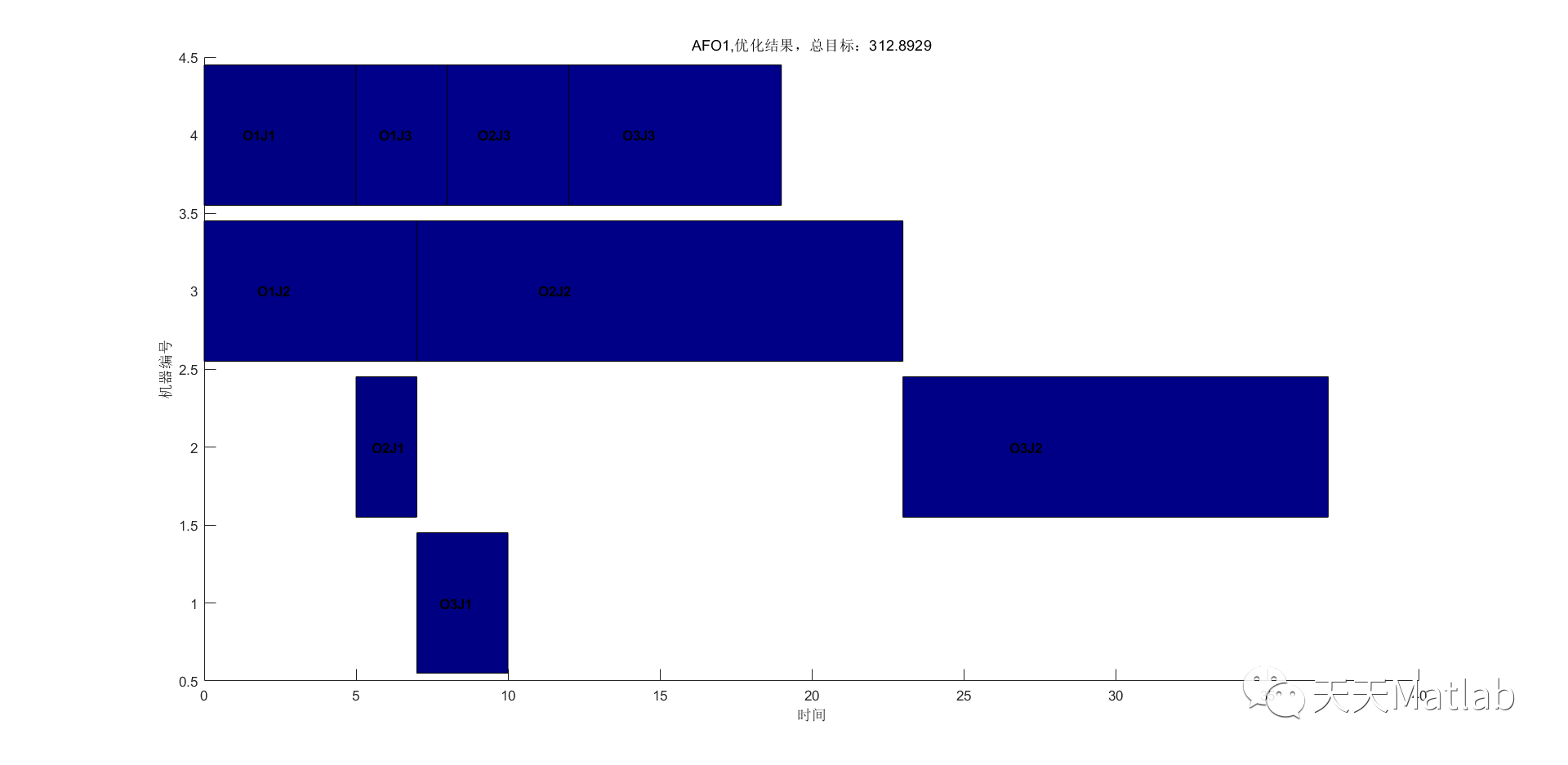
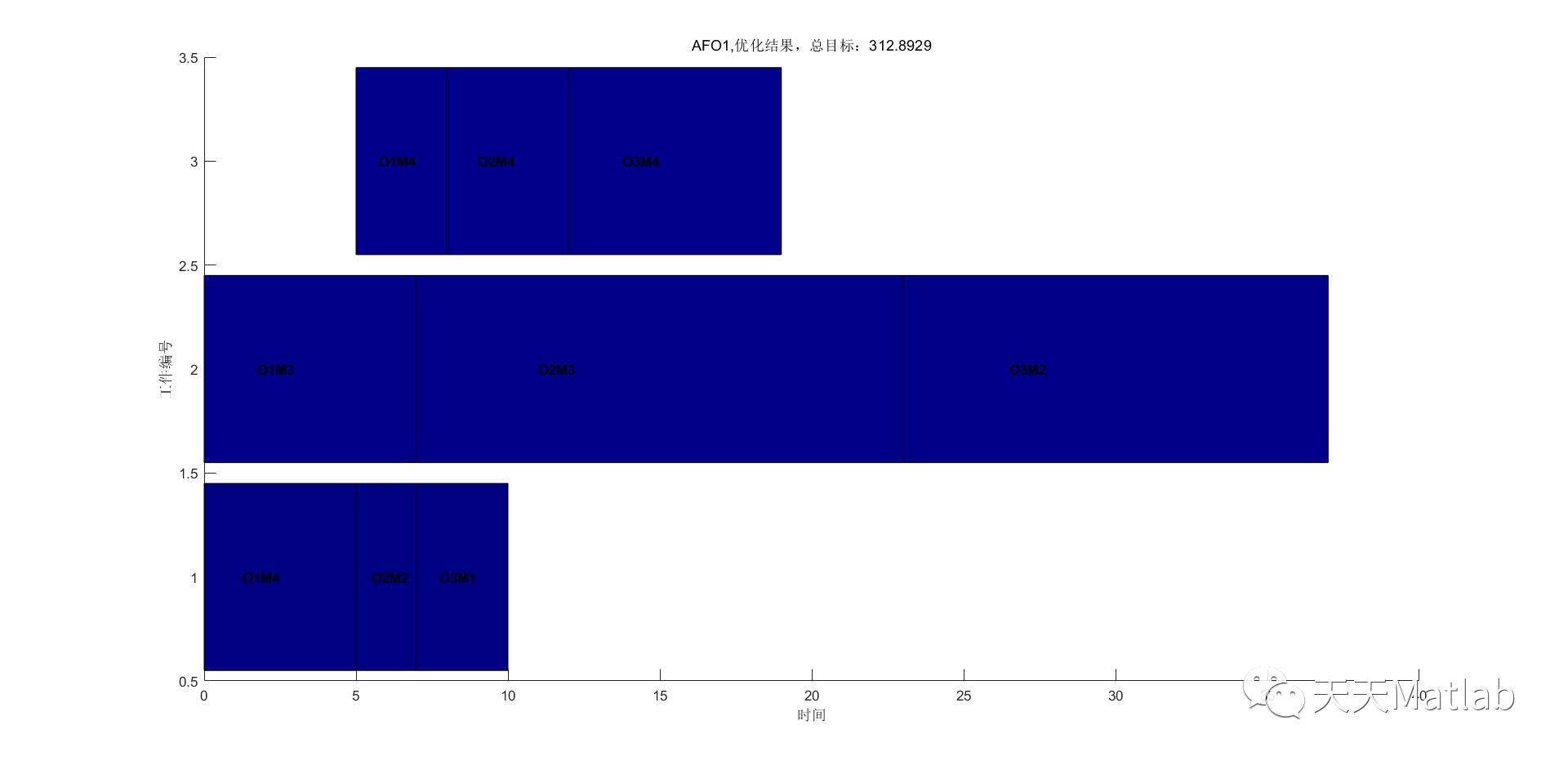
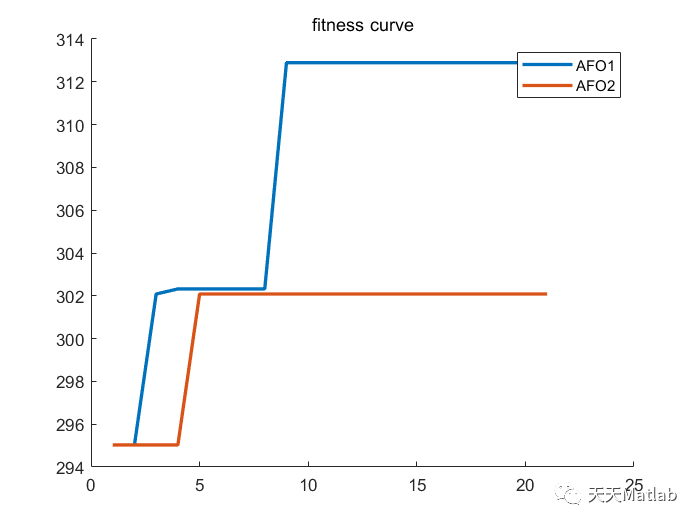
4 参考文献
[1]杨萍. 基于合同网机制的柔性智能车间调度系统建模与仿真. 华南理工大学.
[2]李明, 雷德明. 基于新型帝国竞争算法的高维多目标柔性作业车间调度[J]. 控制理论与应用, 2019, 36(6):9.
[3]张国辉等. "一种改良的帝国竞争算法解决柔性作业车间调度问题的方法.", CN107479522B. 2018.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。





 本文探讨了柔性作业车间调度的复杂性,提出将蚁群算法原理应用于静态调度问题中,以最小化最大完工时间为优化目标。通过建立旅行商问题模型并采用帝国企鹅算法求解,展示了仿真代码和实际求解结果。
本文探讨了柔性作业车间调度的复杂性,提出将蚁群算法原理应用于静态调度问题中,以最小化最大完工时间为优化目标。通过建立旅行商问题模型并采用帝国企鹅算法求解,展示了仿真代码和实际求解结果。

















 220
220

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










