【水果识别】基于形态学实现水果识别含Matlab源码

 1 简介

数学形态学操作可以分为二值形态学和灰度形态学，灰度形态学由二值形态学扩展而来。数学形态学有2个基本的运算，即腐蚀和膨胀，而腐蚀和膨胀通过结合又形成了开运算和闭运算。
开运算就是先腐蚀再膨胀，闭运算就是先膨胀再腐蚀。

1 二值形态学
粗略的说，腐蚀可以使目标区域范围“变小”，其实质造成图像的边界收缩，可以用来消除小且无意义的目标物。式子表达为：

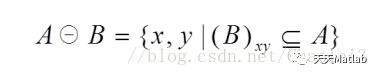
该式子表示用结构B腐蚀A，需要注意的是B中需要定义一个原点，【而B的移动的过程与卷积核移动的过程一致，同卷积核与图像有重叠之后再计算一样】当B的原点平移到图像A的像元(x,y)时，如果B在（x,y）处，完全被包含在图像A重叠的区域，(也就是B中为1的元素位置上对应的A图像值全部也为1)则将输出图像对应的像元(x,y)赋值为1，否则赋值为0。
我们看一个演示图。

B依顺序在A上移动（和卷积核在图像上移动一样，然后在B的覆盖域上进行形态学运算），当其覆盖A的区域为[1,1;1,1]或者[1,0;1,1]时，（也就是B中‘1’是覆盖区域的子集）对应输出图像的位置才会为1。

2 膨胀
粗略地说，膨胀会使目标区域范围“变大”，将于目标区域接触的背景点合并到该目标物中，使目标边界向外部扩张。作用就是可以用来填补目标区域中某些空洞以及消除包含在目标区域中的小颗粒噪声。

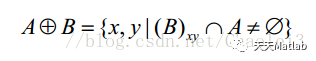
该式子表示用结构B膨胀A，将结构元素B的原点平移到图像像元(x,y)位置。如果B在图像像元(x,y)处与A的交集不为空（也就是B中为1的元素位置上对应A的图像值至少有一个为1），则输出图像对应的像元(x,y)赋值为1，否则赋值为0。
演示图为：

3 小结
也就是说无论腐蚀还是膨胀，都是把结构元素B像卷积操作那样，在图像上平移，结构元素B中的原点就相当于卷积核的核中心，结果也是存储在核中心对应位置的元素上。只不过腐蚀是B被完全包含在其所覆盖的区域，膨胀时B与其所覆盖的区域有交集即可。

4 灰度形态学
在讲述灰度值形态学之前，我们进行一个约定，即将结构元素B覆盖住的图像A的区域记为P（取Part之意）。

5 灰度形态学的腐蚀
那么灰度形态学中的腐蚀就是类似卷积的一种操作，用P减去结构元素B形成的小矩形，取其中最小值赋到对应原点的位置即可。
我们来看一个实例，进行加深对灰度形态学的理解。
假设我们有如下的图像A和结构元素B：

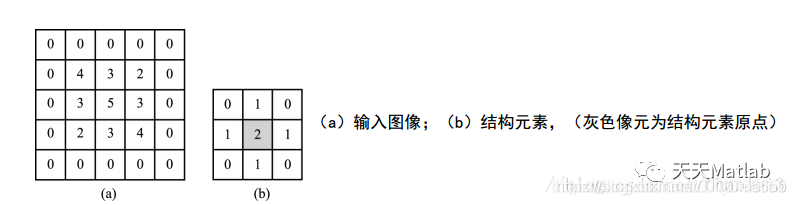
进行灰度形态学腐蚀的过程如下：

我们对输出图像的第一个元素的输出结果进行具体的展示，也就是原点对应的4的位置。输出图像其他的元素的值也都是这样得到的。我们会看到，B首先覆盖的区域就是被减数矩阵，然后在其差矩阵中求min（最小值）来作为原点对应位置的值。

灰度形态学的膨胀
根据上面对腐蚀的描述，我们对膨胀做出同样的描述，灰度形态学中的膨胀就是类似卷积的一种操作，用P加上B，然后取这个区域中的最大值赋值给结构元素B的原点所对应的位置。


这里也对输出图像第一个元素值的来历做个说明。

对上面矩阵的和求最大值就是6，所以把6赋值给结构元素原点所对应的位置。​

2 部分代码

function tfeat = get_features(colorimg, mask)% 特征提取函数 hsvimg = rgb2hsv(colorimg); h = hsvimg(:,:,1); mask1 = mask(:); index = mask1>0;[counts,x] = imhist(h(index));                      %绘制直方图Hue = find(counts == max(counts)); ​% ShapeValue = regionprops(mask, 'majoraxislength','minoraxislength');% Shape = ShapeValue.MajorAxisLength/ShapeValue.MinorAxisLength;ShapeValue = regionprops(mask, 'eccentricity');Shape = ShapeValue.Eccentricity;tfeat = [Hue, Shape ];%tfeat = [feat1 feat2 f.Orientation f2.Eccentricity f1.Extent];

3 仿真结果

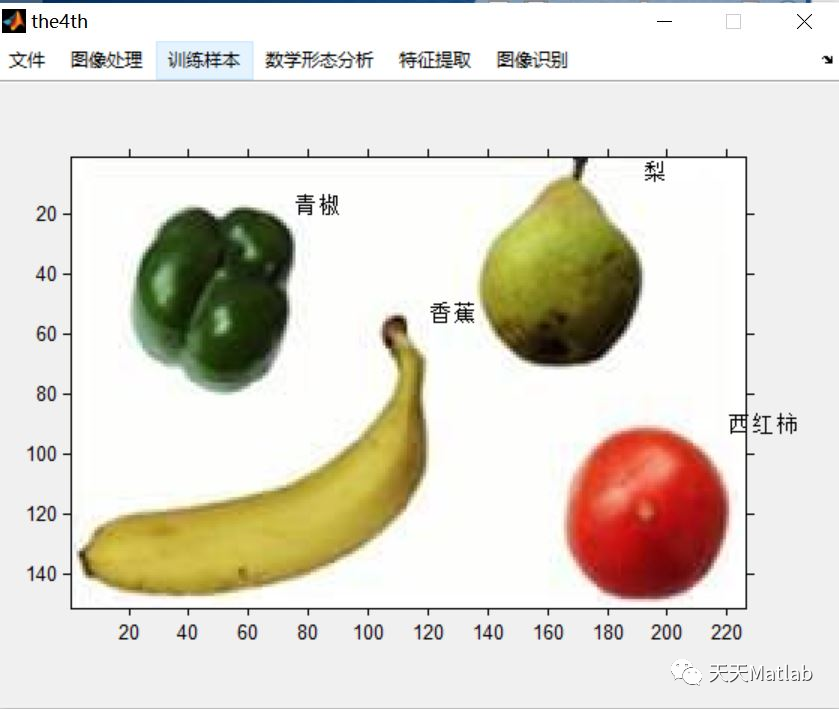
4 参考文献

[1]杨霈. 基于matlab GUI的水果识别系统[J]. 电子制作, 2021(12):2.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。