先充电后协作的安全资源分配

先充电后协作：基于无线能量传输的无线供能中继网络中的安全资源分配

摘要

本文研究了一种无线供能中继网络中的资源分配问题，其中具有恒定能量供应的混合中继协助能量受限源在存在窃听者的情况下向目的地发送机密信息。我们提出了一种新颖的传输协议，称为先充电后协作，以支持该网络中的安全通信。具体而言，在能量传输阶段，混合中继为源节点充电；随后，中继将来自源的机密信息转发至目的地，同时注入干扰信号以对抗窃听。我们的目标是通过联合优化功率分配和时间分配来最大化系统的保密速率。为求解所建立的高度非凸问题，我们设计了一种高效的双层优化算法，该算法结合了一维搜索、交替优化方法、逐次凸逼近技术和拉格朗日对偶方法。仿真结果表明，所提方案能够保证令人满意的保密速率。

索引术语

协同干扰，非凸优化，资源分配，无线供能中继网络。

一、引言

射频（RF）能量收集（EH）技术已成为延长能量受限网络（如物联网[1],[2]）寿命的一种有前景的方法。为了克服能量稀缺并提高网络覆盖范围，RF‐EH技术的一个重要应用是无线供能中继网络（WPRNs），该网络包括两类：源供能中继型WPRN和中继供能源型WPRN[3]。在源供能中继型WPRN中，配备有能量收集电路的中继首先从源（例如接入点）发射的射频信号中收集能量，然后将信号转发至目的地[4]。在中继供能源型WPRN中，能量充足的中继通过无线能量传输为能量受限的源（例如传感器）充电，随后协助信息从源到目的地的传输[5]。

由于无线通信信道具有开放性，天然容易受到窃听，因此在WPRNs中实现安全通信已成为亟需解决的关键问题。最近，作为候选物理层安全方法之一的协同干扰（CJ）技术已被广泛研究。通过注入干扰信号来迷惑窃听者，以保障安全通信，这一方法已被研究[6]。具体而言，[7]中的作者研究了发射机与接收机之间的安全通信，其中全双工干扰器利用其收集的能量发送干扰信号，以降低窃听者的接收信号质量。在[8]中，提出了一种在无线供电通信网络中使用的先积累后传输协议，其中功率信标首先向能量受限源传输能量，然后作为协作干扰器，保护源的机密信息免受窃听。此外，在WPRN中实施协作干扰技术已引起广泛关注，被视为应对能量稀缺和安全脆弱性的有效解决方案。特别是，[9]中的作者采用了一种目的辅助干扰方法，用于确保两跳WPRN中的安全通信，其中中继节点能量匮乏，并从其接收到的信号中收集能量。为了最大化能量采集式中继网络中的保密速率，[10]提出了一种自适应协作干扰方案，能够自适应地确定功率分配因子。[11]中的作者采用了一种源辅助干扰方法，并在一种中继具备能量收集能力且为不可信中继的WPRN中，开发了一种自适应协作安全方案。然而，这些工作均考虑了源供能中继型WPRN中的物理层安全。据我们所知，针对中继供能源型WPRN的安全通信研究尚未开展。值得指出的是，在WPRN中必须满足著名的能量因果约束，以确保节点收集的能量超过其消耗的能量。该关键约束在两类网络中分别施加于中继和源，因此源供能中继型WPRN中的安全传输方案不适用于中继供能源型WPRN。研究中继供能源型WPRN中安全通信的挑战主要包括以下两个方面：首先，由于存在多个传输阶段以及能量因果约束，每个传输阶段分配的时间与源的发射功率之间具有强耦合关系，不可避免地导致资源分配问题难以处理；其次，由于无线通信的广播特性，从源发送到中继、再由中继转发至目的地的机密信息容易受到窃听。因此，有必要研究如何在中继供能源型WPRN中利用协作干扰技术防止机密信息被窃听。

受上述讨论的启发，本文研究基于中继供能源的WPRN中的安全资源分配问题。通过采用RF‐EH和CJ技术，我们提出了一种新颖的先充电后协作（CTC）传输协议，该协议应用于能量充足的混合中继。在该协议中，中继通过无线能量传输为能量匮乏的源节点充电，随后将源节点的机密信息转发至目的地，同时作为友好干扰器对窃听者进行干扰。我们的目标是通过联合优化功率分配和时间分配来最大化系统的保密速率。所建立的问题具有高度非凸性，因此我们提出一种高效的双层优化算法来求解该问题。具体而言，我们将原问题分解为内层功率分配问题和外层时间分配问题。对于非凸的内层问题，采用交替优化方法将其转化为两个子问题，其中发射功率优化子问题仍为非凸问题。为解决这一难题，应用逐次凸逼近（SCA）技术将发射功率优化子问题近似转化为凸问题，并利用拉格朗日对偶方法进行求解。外层时间分配问题则通过一维搜索方法求解。数值结果表明，与其他方案相比，所提方案在保密速率方面具有显著增益。

II. 系统模型与问题表述

A. 系统模型

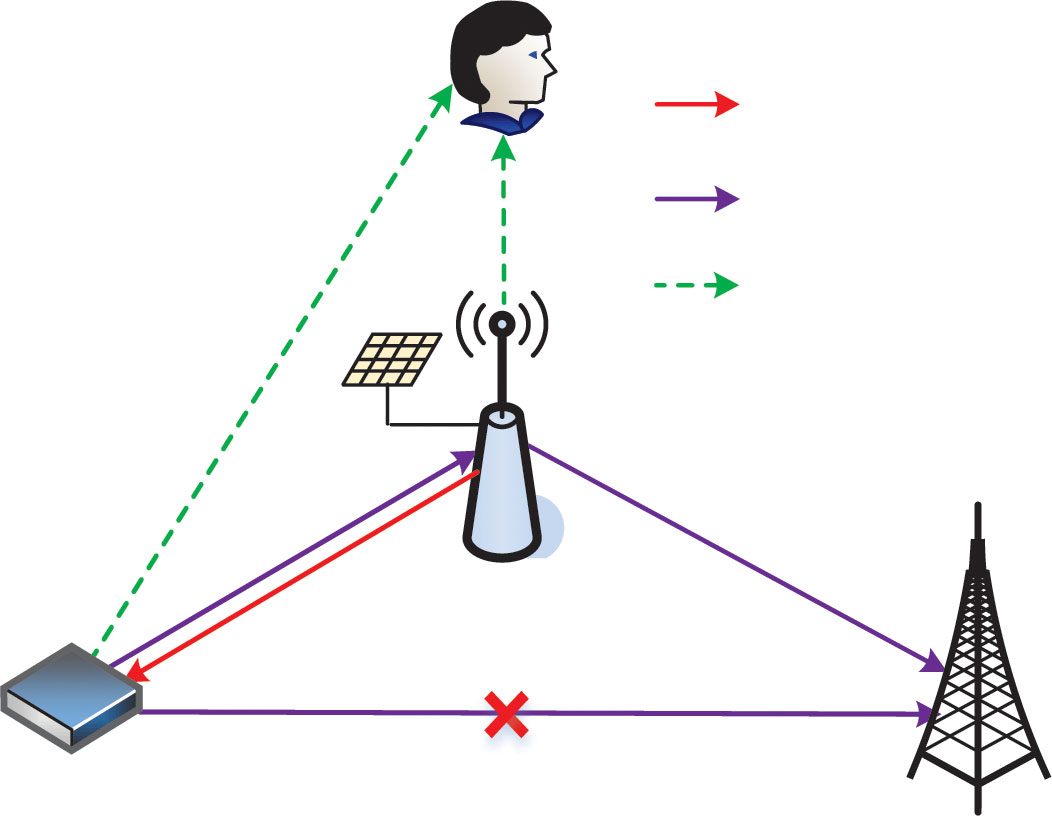
如图1所示，我们考虑一个无线功率受限网络（WPRN），其中源 S在混合中继 R的协助下向目的地 D发送机密信息，同时与一个窃听者 E共存。类似于[12]中的假设，由于物理障碍的存在，不存在直连源‐目的地链路。在所考虑的系统中，S由于尺寸较小（例如传感器）而处于能量受限状态，并且可以由具有恒定能量供应的混合中继R供电。所有信道为准静态平坦衰落，在一个传输块内保持不变，但在不同的传输块之间独立变化[13]。我们将hi、j表示为节点 i与节点 j之间的信道系数，满足信道互易性，其中hi、j= hj、i和(i, j) ∈{(R, S)、(S, R)、(S, E)、(R, D)、(R, E)}。假设完美信道状态信息（CSI）可用。特别地，当 E在网络中处于活跃状态时，可以获得与窃听者 E相关的CSI，即窃听者也是当前网络中的一个活跃用户（例如时分多址网络），因此其CSI可在其传输过程中获得[14],[15]。

在此网络中，我们提出了一种新的应用于 R的CTC协议，以增强安全通信。具体而言，R除了向 S传输能量外，还充当辅助节点，将来自 S的机密信息转发至 D，同时作为友好干扰器，通过发送干扰信号对 E进行干扰。相应地，S采用传统的先收集后传输协议，以延长所考虑网络的寿命。在此背景下，每个传输块中的整个传输被划分为三个阶段。不失一般性，假设每个传输块的长度等于1。随后，各阶段详细说明如下。

1) 第一阶段：由于 S是一个具有能量收集能力的能量受限节点，在此阶段，能量充足的 R采用无线能量传输技术，在持续时间为 α的时间内为 S供电。因此，S收集的能量可表示为[16]

$$
E_{S,1} = \eta\alpha P_{R,1}|h_{R,S}|^2, \quad (1)
$$

其中 $0 \leq \eta \leq 1$ 是能量转换效率，$P_{R,1}$ 是 R在第一阶段发送无线能量时的发射功率。

2) 第二阶段：由于窃听者 E意图通过窃听信道窃听源发送的机密信息 S,E，源利用收集的能量在持续时间为 β的时间内广播其保密信号以及干扰信号x, z和 E处的接收信号可分别表示为

$$
y_R = (\sqrt{P_{S,2}}x + \sqrt{P_{jS,2}}z)h_{S,R} + N_R
$$

以及

$$
y_E = (\sqrt{P_{S,2}}x + \sqrt{P_{jS,2}}z)h_{S,E} + N_E。
$$

其中，$P_{S,2}$ 分别表示 S用于发送保密信号和干扰信号的发射功率，$N_R$ 是 R处的加性高斯白噪声(AWGN)，$N_E$ 是 E处的加性高斯白噪声(AWGN)。注意，干扰信号仅由 R已知，可通过文献[16]中的方法实现。在 R处干扰信号被抵消后，R处的接收信噪比(SNR)以及 E处的信号干扰噪声比(SINR)可分别表示为

$$
\gamma_{R,2} = \frac{P_{S,2}|h_{S,R}|^2}{\sigma^2_R}, \quad (2)
$$

$$
\gamma_{E,2} = \frac{P_{S,2}|h_{S,E}|^2}{P_{jS,2}|h_{S,E}|^2 + \sigma^2_E}. \quad (3)
$$

其中 $\sigma^2_R$ 和 $\sigma^2_E$ 分别是中继和窃听者的噪声功率。此外，我们假设在 S收集的能量仅用于信息传输。在此基础上，应满足源节点 S的能量因果约束，即

$$
P_{S,2}\beta + P_{jS,2}\beta \leq \eta\alpha P_{R,1}|h_{R,S}|^2。
$$

3) 第三阶段：在持续时间为 β的最后阶段，R采用解码转发 (DF)方法进行协作通信。实际上，当 R向D转发机密信息时，E也可以通过窃听信道$h_{R,E}$对其进行窃听。为了实现安全通信，R同时充当友好干扰器，发送干扰信号以干扰 E。因此，D处接收到的信噪比（SNR）以及 E处接收到的信干噪比（SINR）分别为

$$
\gamma_{D,3} = \frac{P_{rR,3}|h_{R,D}|^2}{\sigma^2_D}, \quad (4)
$$

$$
\gamma_{E,3} = \frac{P_{rR,3}|h_{R,E}|^2}{P_{jR,3}|h_{R,E}|^2 + \sigma^2_E}, \quad (5)
$$

其中，$P_{rR,3}$ 是 R用于将机密信息从 S转发到 R的发射功率，$P_{jR,3}$ 表示 R注入干扰信号的发射功率，$\sigma^2_D$ 是目的地的噪声功率。注意，R的干扰信号可通过[17]中的相同方法被 D获知。

总之，窃听者 E在第二阶段和第三阶段窃听了 S的机密信息。为了增强在整个过程中的窃听能力，E采用最大比合并（MRC）技术。因此，我们可以将 E的窃听速率表示为

$$
R_E = \beta \log_2\left(1 + \frac{P_{S,2}|h_{S,E}|^2}{P_{jS,2}|h_{S,E}|^2 + \sigma^2_E} + \frac{P_{rR,3}|h_{R,E}|^2}{P_{jR,3}|h_{R,E}|^2 + \sigma^2_E}\right). \quad (6)
$$

通过采用DF方法，合法信道的端到端可达速率由最弱的链路决定。因此，它可以表示为

$$
R_D = \beta \min\left{\log_2\left(1 + \frac{P_{S,2}|h_{S,R}|^2}{\sigma^2_R}\right), \log_2\left(1 + \frac{P_{rR,3}|h_{R,D}|^2}{\sigma^2_D}\right)\right}. \quad (7)
$$

相应地，D的可达保密速率可以表示为

$$
R_s = [R_D - R_E]^+, \quad (8)
$$

其中 $[x]^+ = \max{0, x}$。

B. 问题表述

在本研究中，我们旨在通过联合优化 S和 R处的功率分配以及保密速率来最大化系统的保密速率。相应地，该优化问题可以数学表述为

$$
\text{P1:} \quad \max_{P_{S,2}, P_{jS,2}, P_{rR,3}, P_{jR,3}, \alpha, \beta} [R_D - R_E]^+ \quad (9a)
$$

s.t.
$$
P_{S,2}\beta + P_{jS,2}\beta \leq \eta\alpha P_{R,1}|h_{R,S}|^2, \quad (9b)
$$
$$
P_{rR,3}\beta + P_{jR,3}\beta \leq P_B, \quad (9c)
$$
$$
\alpha + 2\beta = 1, \quad (9d)
$$
$$
P_{S,2} \geq 0, \quad P_{jS,2} \geq 0, \quad P_{rR,3} \geq 0, \quad P_{jR,3} \geq 0, \quad (9e)
$$
$$
0 \leq \alpha \leq 1, \quad (9f)
$$
$$
0 \leq \beta \leq \frac{1}{2}, \quad (9g)
$$

其中，(9b) 确保 S 处的消耗的能量不超过收集的能量，(9c) 对 R 处的最大功率预算 $P_B$ 施加限制，(9d)-(9g) 为功率分配和时间分配约束条件。问题 P1 是非凸的，难以直接求解。此外，(9a)、(9b) 和 (9c) 中变量的强耦合使得该问题更具挑战性。

III. 功率分配与时间分配的联合优化

在本节中，我们提出了一种高效的双层优化算法来求解P1。具体而言，我们首先利用双层优化的概念，将P1分解为一个内层功率分配问题和一个外层时间分配问题。内层问题对应于在给定时间分配因子的情况下，关于功率分配变量的保密速率最大化问题。外层问题对应于关于时间分配变量的系统保密速率最大化问题。即，P1可以等价地重新表述为如下嵌套形式：

$$
\text{P}‘1: \quad \max_{\alpha,\beta} R_s(\alpha, \beta), \quad \text{s.t.} (9d), (9f), \text{and} (9g),
$$

其中
$$
\text{P}’‘1: \quad R_s(\alpha, \beta) = \max_{P_{S,2}, P_{jS,2}, P_{rR,3}, P_{jR,3}} [R_D - R_E]^+
$$
s.t. (9b), (9c), and (9e).

针对上述问题，我们首先在给定P′′ 1 和 α的条件下求解 β，然后由于 β的存在，退而采用关于 α+2β=1的一维搜索。具体而言，将 β的可行范围划分为相等的区间，即 β ∈{0,…, iΔβ,…, 1/2} ，其中 i= 0,…, 1/(2Δβ) ，且 Δβ为粒度。对于内层问题P′′ 1 ，发射功率变量之间的强耦合使得该问题仍然难以求解。为了克服这一困难，我们采用交替优化方法，并将功率分配变量划分为两个块：一个用于发送机密信息，另一个用于发送干扰信号。相应地，需要求解两个发射功率优化子问题。需要注意的是，这两个子问题将被迭代优化，直到达到满意的收敛性为止。接下来，我们将详细介绍这两个子问题的求解过程。

A. 发射功率优化以发送机密信息

在第一个子问题中，我们通过假设${P_{jS,2}, P_{jR,3}}$ 已知来优化 ${P_{S,2}, P_{rR,3}}$，从而得到表示为的首个子问题

$$
\text{P2:} \quad \max_{P_{S,2}, P_{rR,3}} \beta[\min{\log_2(1 + a_1 P_{S,2}), \log_2(1 + a_2 P_{rR,3})} - \log_2(1 + a_3 P_{S,2} + a_4 P_{rR,3})]
$$

s.t. (9b), (9c), $P_{S,2} \geq 0$, $P_{rR,3} \geq 0$,

其中 $a_1 = \frac{|h_{S,R}|^2}{\sigma^2_R}$, $a_2 = \frac{|h_{R,D}|^2}{\sigma^2_D}$, $a_3 = \frac{|h_{S,E}|^2}{P_{jS,2}|h_{S,E}|^2 + \sigma^2_E}$, 以及 $a_4 = \frac{|h_{R,E}|^2}{P_{jR,3}|h_{R,E}|^2 + \sigma^2_E}$为方便起见而引入。我们注意到，目标函数的最优值必须是非负的，这意味着问题P2无论是否包含正部操作[·]+，其最优值和解均相同。因此，在后续推导中省略了P2目标函数中的正部操作。

由于目标函数是两个对数函数的差，P2是一个非凸优化问题。为了求解问题P2, ，我们首先引入一个新变量 $R = \min{\log_2(1+a_1P_{S,2}), \log_2(1+a_2P_{rR,3})}$来处理目标函数中的最大最小操作。然而，由于（6）式中窃听信道速率形式复杂，目标函数仍然难以处理。为解决此问题，我们随后采用SCA技术[18],[19]。具体而言，通过利用该函数的一阶泰勒展开，可将目标函数中的$-\log_2(1+ a_3P_{S,2}+ a_4P_{rR,3})$转化为凸函数。在给定满足P2,约束条件的可行解$P’ {S,2}$和$P’ {rR,3}$的情况下，我们得到

$$
-\log_2(1+a_3P_{S,2}+a_4P_{rR,3}) \geq -\log_2(1+a_3P’ {S,2}+a_4P’ {rR,3})
- \frac{a_3(P_{S,2}- P’ {S,2})}{(1+ a_3P’ {S,2}+ a_4P’ {rR,3}) \ln2}
- \frac{a_4(P {rR,3} - P’ {rR,3})}{(1+ a_3P’ {S,2}+ a_4P’_{rR,3}) \ln2}.
\quad (10)
$$

因此，P2可以近似转换为以下表示的优化问题

$$
\text{P’}2: \quad \max_{P_{S,2}, P_{rR,3}, R} \beta(R - b_1P_{S,2} - b_2P_{rR,3} + b_3) \quad (11a)
$$

s.t. (9b), (9c), $P_{S,2} \geq 0$, $P_{rR,3} \geq 0$, (11b)
$R \leq \log_2(1+ a_1P_{S,2})$, (11c)
$R \leq \log_2(1+ a_2P_{rR,3})$, (11d)
$R \geq 0$, (11e)

where
$b_1 = \frac{a_3}{(1+a_3P’ {S,2}+a_4P’ {rR,3})\ln2}$,
$b_2 = \frac{a_4}{(1+a_3P’ {S,2}+a_4P’ {rR,3})\ln2}$, and
$b_3 = \frac{a_3P’ {S,2}+a_4P’ {rR,3}}{(1+a_3P’ {S,2}+a_4P’ {rR,3})\ln2} - \log_2(1+ a_3P’ {S,2} + a_4P’ {rR,3})$ are used for the sake of notational simplicity.

引理1 ：给定$P_{S,2}$和$P_{rR,3}$，P′2 中的目标函数是P2 中目标函数的紧下界。

证明 ：P2 和P′2 中的目标函数分别表示为 $f(P_{S,2}, P_{rR,3})$和 $f(P_{S,2}, P_{rR,3}, P’ {S,2}, P’ {rR,3})$。利用(10)式中的不等式，可得 $f(P_{S,2}, P_{rR,3}) \geq f(P_{S,2}, P_{rR,3}, P’ {S,2}, P’ {rR,3})$。此外，若$P_{S,2} = P’ {S,2}$ 且$P {rR,3} = P’ {rR,3}$，则有 $f(P {S,2}, P_{rR,3}) = f(P_{S,2}, P_{rR,3}, P’ {S,2}, P’ {rR,3})$。即P′2中的目标函数为P2 中目标函数的紧下界。□

可以看出，P′2 是一个凸优化问题。接下来，我们基于拉格朗日对偶方法为P′2 推导出一个闭式解。为此，拉格朗日函数可表示为

$$
L(P_{S,2}, P_{rR,3}, R, \lambda, \mu, \phi, \varphi)
= \beta(R - b_1 P_{S,2} - b_2 P_{rR,3} + b_3) - \lambda(P_{S,2} \beta - \eta\alpha P_{R,1}|h_{R,S}|^2)
- \mu(P_{rR,3}\beta + P_{jR,3}\beta - P_B) - \phi(R - \log_2(1+ a_1P_{S,2}))
- \varphi(R - \log_2(1+ a_2P_{rR,3})), \quad (12)
$$

其中 $\lambda$、$\mu$、$\phi$ 和 $\varphi$ 分别是与P′2中的(9b)、(9c)、(11c)和(11d)相关的非负拉格朗日乘子。然后，对偶函数可表示为

$$
G(\lambda, \mu, \phi, \varphi) = \min_{\lambda,\mu,\phi,\varphi \geq 0} \max_{P_{S,2}, P_{rR,3}, R \geq 0} L(P_{S,2}, P_{rR,3}, R, \lambda, \mu, \phi, \varphi). \quad (13)
$$

通过拉格朗日对偶分解，(13)中的对偶问题可以分解为两层。第一层是涉及计算$P_{S,2}$, $P_{rR,3}$和 $R$的内层最大化问题。第二层是对偶变量更新的外层最小化问题。

由于P′2是一个凸优化问题，最优解满足第一层内层最大化问题的卡鲁什‐库恩‐塔克（KKT）条件。对$L$关于$P_{S,2}$、$P_{rR,3}$、$R$分别求一阶偏导数，并应用KKT条件，我们得到

$$
\frac{\partial L}{\partial P_{S,2}} = - b_1\beta - \lambda\beta + \frac{\phi a_1}{(1+ a_1P_{S,2}) \ln2} = 0, \quad (14)
$$

$$
\frac{\partial L}{\partial P_{rR,3}} = - b_2\beta - \mu\beta + \frac{\varphi a_2}{(1+ a_2P_{rR,3}) \ln2} = 0, \quad (15)
$$

$$
\frac{\partial L}{\partial R} = \beta - \phi - \varphi = 0. \quad (16)
$$

因此，可以得到P′2的闭式解

$$
P^*_{S,2} = \left[ \frac{\phi}{(b_1\beta + \lambda\beta) \ln2} - \frac{1}{a_1} \right]^+, \quad (17)
$$

$$
P^{r*}_{R,3} = \left[ \frac{\varphi}{(b_2\beta + \mu\beta) \ln2} - \frac{1}{a_2} \right]^+, \quad (18)
$$

其中 $\varphi = \beta - \phi$通过利用(16)得到。

为了解决式(13)中的外层最小化问题，采用次梯度法来更新对偶变量。因此，该更新可表示为

$$
\lambda^{(n+1)} = [\lambda^{(n)} - \zeta^{(n)} 1 \times (\eta\alpha P {R,1}|h_{R,S}|^2 - P^*_{S,2} \beta)]^+,
$$

$$
\mu^{(n+1)} = [\mu^{(n)} - \zeta^{(n)} 2 \times (P_B - (P^{r*} {R,3} \beta + P_{jR,3} \beta))]^+,
$$

$$
\phi^{(n+1)} = [\phi^{(n)} - \zeta^{(n)}_3 \times (\log_2(1+ a_1P^ _{S,2}) - R^ )]^+, \quad (19)
$$

其中 $n \geq 0$为迭代索引，$\zeta^{(n)}_i$（i= 1,2, 3）表示第 n次迭代时的正迭代步长。

总之，求解P2的整体流程在算法1中给出。实际上，所提算法1的本质是基于SCA技术和拉格朗日对偶方法求解P2。

定理1 : 所提算法1保证在有限次迭代内收敛。

证明 ：请参阅附录。 □

B. 干扰信号发射功率优化

在给定${P_{S,2}, P_{rR,3}}$的情况下，我们随后通过优化${P_{jS,2}, P_{jR,3}}$来求解第二个子问题。相应地，P′′1 的第二个子问题可表示为

$$
\text{P3:} \quad \max_{P_{jS,2}, P_{jR,3}} \beta[\min{\log_2(1+ a_1 P_{S,2}), \log_2(1+ a_2 P_{rR,3})}
- \log_2\left(1+ \frac{P_{S,2}|h_{S,E}|^2}{P_{jS,2}|h_{S,E}|^2+\sigma^2_E} + \frac{P_{rR,3}|h_{R,E}|^2}{P_{jR,3}|h_{R,E}|^2+\sigma^2_E}\right)]^+
$$

s.t. (9c), $P_{jS,2} \geq 0$, $P_{jR,3} \geq 0$.

为了获得最优解，我们首先对P3中的约束条件进行数学变换，得到
$0 \leq P_{jS,2} \leq \left[\frac{\eta\alpha P_{R,1} |h_{R,S}|^2 - P_{S,2}\beta}{\beta}\right]^+$ 和
$0 \leq P_{jR,3} \leq \left[\frac{P_B - P_{rR,3} \beta}{\beta}\right]^+$。
由于P3中的目标函数关于 $P_{jS,2}$ 和 $P_{jR,3}$ 是非递减的，因此P3的最优解可表示为

$$
P^{j*} {S,2} = \left[\frac{\eta\alpha P {R,1}|h_{R,S}|^2 - P_{S,2}\beta}{\beta}\right]^+, \quad (20)
$$

$$
P^{j*} {R,3} = \left[\frac{P_B - P {rR,3} \beta}{\beta}\right]^+. \quad (21)
$$

然后，求解问题P′′1 的整体流程在算法2中给出。算法2中${P^{(0)} {S,2}, P^{j(0)} {S,2}, P^{r(0)} {R,3}, P^{j(0)} {R,3}}$的初始化必须满足P′′1 的所有约束条件。具体而言，我们通过将 S所收集的能量进行均等分配来初始化功率分配${P^{(0)} {S,2}, P^{j(0)} {S,2}}$，并通过将 R的功率预算进行均等分配来初始化功率分配${P^{r(0)} {R,3}, P^{j(0)} {R,3}}$。所提算法的核心是通过迭代方式交替求解子问题P2 和P3 来优化变量。值得指出的是，在经典交替优化方法中，每个子问题都需要最优求解以保证收敛性。然而，对于第一个子问题P2，我们仅求解其近似问题P′2。因此，经典交替优化方法的收敛性分析不能直接适用。随后，我们给出定理2以说明算法2的收敛性。

定理2 ：所提算法2保证在有限次迭代内收敛。

证明 ：请参见附录。 □

C. 复杂度与最优性分析

如前所述，通过使用所提双层优化算法，问题P1可分解为内层功率分配问题P′′1和外层时间分配问题P′1。对于P′1，采用一维搜索方法求解，因此其相应复杂度可表示为 $O\left(\frac{1}{2\Delta\beta}+1\right)$。内层问题P′′1通过算法2求解，其本质是交替优化方法。因此，算法2 的复杂度是求解子问题P2和P3的复杂度的线性组合。由于P2通过SCA方法和拉格朗日对偶方法利用算法1求解，而P3通过闭式解求解，因此求解P′′1的复杂度可写为 $O((N_2 \cdot \log_2(1/\varepsilon_0)+1)K)$，其中 $N$为对偶变量数量，$\varepsilon_0$表示算法1收敛所需的精度，$K$表示算法2的迭代次数。因此，求解原始问题P1的总体复杂度为 $O\left(\left(\frac{1}{2\Delta\beta}+1\right)((N^2 \cdot \log_2(1/\varepsilon_0)+1)K\right)$。随后，我们分析所提双层优化算法的最优性特性。由于内层问题P′′1通过基于子问题P′2和P3的最优解迭代更新变量进行近似求解，因此算法2得到的是P′′1的次优解。此外，外层问题P′1可通过一维搜索方法最优求解。在仿真中，我们将进一步证明所提算法实现的保密速率可以接近最优保密速率。

IV. 数值结果

本节展示了仿真结果，以验证所提出的安全资源分配方案的有效性。本文考虑的网络拓扑与[6]类似，节点 i与节点 j之间的距离在$(i, j) \in {(S, R)、(S, E)、(R, D)、(R, E)}$情况下分别设为$d_{S,R}=3$ m，$d_{R,D}=3$ m，$d_{S,E}=8$ m以及$d_{R,E}=6$ m。所考虑网络中的信道功率增益建模为$|h_{i,j}|^2 = \theta_{i,j} d^{-m} {i,j}$，其中 $d {i,j}$表示节点 i与节点 j之间的距离，$m$表示路径损耗指数，$\theta_{ij}$表示均值为1的指数分布随机变量。除非另有说明，我们设定能量转换效率为$\eta= 0.5$，噪声功率为$\sigma^2_R = \sigma^2_E = \sigma^2_D = -60$ dBm，R发送无线能量的发射功率为$P_{R,1}=20$ dBm，最大功率预算为$P_B=35$ dBm，路径损耗指数为 $m=3$，粒度为$\Delta\beta= 10^{-4}$。

为评估所提方案的性能，我们将该方案与以下基线方案进行比较：1）在[14]中的协作干扰辅助中继传输（CJART）方案，其中 R作为协作干扰器，通过发送干扰信号来迷惑窃听者，而 S仅传输其机密信息；2）等时分配（ETA）方案，即每个传输阶段分配的时间量相等；3）固定中继发射功率（FRTP）方案，即该方案为中继源的信息设置恒定的发射功率；4）基于穷尽搜索的安全资源分配（ESSRA）方案，其中采用完全穷尽搜索遍历所有可能的功率分配和时间分配结果。图2展示了在 R与 D之间不同距离下，所提方案与基线方案之间的保密速率对比。图中显示，所有方案的保密速率均随$d_{R,D}$的增加而下降。这一现象由两个原因造成。一方面，随着$d_{R,D}$的增大，D的可达速率下降是直观的，因此合法信道的可达速率也随之降低。另一方面，当距离$d_{R,D}$增加时，R需要将更大比例的发射功率用于将 S的机密信息转发给 D，而用于对抗窃听的发射功率则相应减少。此外，可以观察到，在保密速率方面，所提方案优于CJART方案、ETA方案以及FRTP方案。这可归因于在所提方案中，S和 R的发射功率被动态分配以发送机密信息和干扰信号以及每个传输阶段的时间被灵活分配，这与ETA方案和 FRTP方案不同。此外，[14]中的CJART方案仅关注 R与 D之间的安全传输，而 S与 R之间的保密通信仍然容易受到窃听。与CJART方案相比，所提方案关注两阶段安全通信，其中 S和 R均可发送干扰信号以迷惑窃听者。

图3展示了不同方案下保密速率随发射功率$P_{R,1}$变化的仿真结果。从图3中可以得出三个观察结论。首先，显然随着$P_{R,1}$的增加，所有方案中的保密速率均单调上升。原因是$P_{R,1}$的增加使得 S收集的能量更多，S能够以更高的发射功率发送机密信息和干扰信号，从而有利于提升系统保密速率。其次，保密速率的增长速率逐渐下降。其原因是尽管 S收集的能量已足够，但 R的功率预算成为瓶颈。第三，我们所提方案在保密速率上优于 CJART方案、ETA方案以及FRTP方案。这是因为所提方案联合设计了功率分配与时间分配，并考虑了协作干扰技术的影响，即该方案全面考虑了所有影响系统保密速率的因素。此外，从图2 和图3中可以看出，与ESSRA方案相比，我们提出的方案实现了近最优性能。值得指出的是，ESSRA方案虽然通过指数复杂度达到了上界性能，而所提方案能够在低复杂度下逼近最优保密速率，且通过与其他基线方案的比较验证了其有效性。

V. 结论

本文提出了一种新型的CTC传输协议，以确保在考虑从中继到源节点进行无线能量传输的无线功率受限网络中的安全通信。保密速率在满足源端的能量因果约束和中继端的功率预算约束下，建立了最大化问题。为解决所提问题的难解性，设计了一种高效的双层优化算法。具体而言，通过应用交替优化方法、SCA技术以及拉格朗日对偶方法，推导出了功率分配的闭式表达式。时间分配策略则通过一维搜索方法获得。仿真结果验证了所提方案相较于其他方案的优越性能。在未来工作中，将研究在不完美的窃听信道状态信息和非线性能量收集模型下的安全资源分配问题。