毫米波无开关PALNA损耗优化方法

一种面向无开关PALNA集成电路设计的毫米波损耗感知方法

摘要

相控阵单元射频前端通常采用具有高隔离度的单刀双掷（SPDT）开关或环形器，以防止发射能量泄漏到接收电路中。然而，随着相控阵设计扩展至毫米波频段，并实现高度集成，开关和环形器所带来的物理尺寸及性能退化问题，在满足系统性能量和SWAP要求方面可能带来挑战。本文提出一种考虑损耗的分析方法，用于无开关收发（T/R）电路的分析与设计。该方法提供了设计洞察，并提供了一种实用且普遍适用的方法，以解决无开关功率放大器/低噪声放大器（PALNA）匹配网络的多变量优化问题。该匹配网络在发射和接收两种工作模式下，分别为功率放大器（PA）和低噪声放大器（LNA）提供最佳匹配阻抗，同时最大化功率传输效率并最小化耗散损耗。本文展示了基于格罗方德32SOI CMOS工艺、在W波段应用所提方法的一个设计实例。该设计在94 GHz下实现了18%的最大附加功率效率（仿真值）和7.5 dB的噪声系数（仿真值）。

索引术语 —相控阵，收发（T/R）电路，PALNA，LNAPA，双向T/R电路，无开关T/R电路，功率放大器（PA），低噪声放大器（LNA），噪声系数（NF），附加功率效率（PAE），输出功率（Pout）。

I. 引言

传统相控阵单元射频前端中，单个天线在发射和接收信号链之间共享，使用收发（T/R）开关或环形器来提供所需的隔离度（见图1(a)–1(b)）。然而，随着近年来对集成相控阵电路在毫米波频率下的关注，人们认识到片上集成的T/R开关占据了相当大的芯片面积[1]。同样，铁氧体环形器难以集成，尽管已实现片上无源环形器，但其尚未扩展到94 GHz并具备可接受的损耗性能[2]。因此，人们对消除或创新性地使用T/R开关的收发电路架构的兴趣日益增加[3]‐[15]。

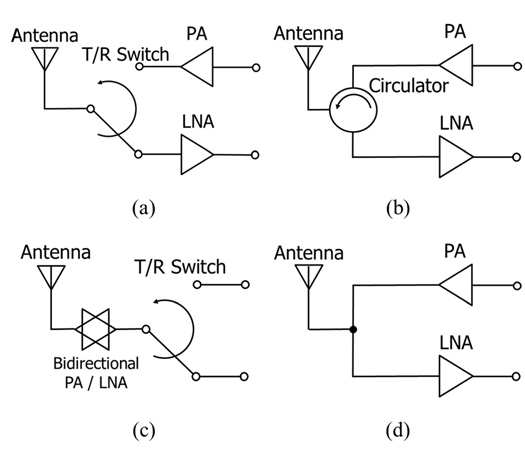
在文献中受到广泛关注的一种电路架构基于双向功率放大器/低噪声放大器（PALNA）概念（见图1(c)）。通过将收发（T/R）开关置于放大器的收发器侧，双向PALNA可降低开关损耗对收发电路整体性能的影响。首个已知的毫米波双向PALNA放大器在[3]和[4]中报道。该放大器利用了共栅放大器拓扑的固有对称性，并且使用相同的器件实现低噪声放大器（LNA）和功率放大器（PA）功能，这可能具有局限性，因为晶体管尺寸无法针对每种功能单独优化。为了实现晶体管尺寸的灵活性，在[5]和[6]中引入了一种共源收发（T/R）电路拓扑，但未提供连接低噪声放大器和功率放大器电路的匹配网络设计细节。在[3]‐[6]中报道的电路采用砷化镓（GaAs）工艺制造，最近还展示了磷化铟（InP）的实现方案[7]。然而，近年来对使用硅实现毫米波相控阵收发（T/R）电路的兴趣日益增加，已出现了基于硅的双向PALNA收发电路实现[8]‐[13]。

在[8]和[9]中，报道了一种基于时分双工方法的双端口PALNA电路，其中通过偏置切换交替开启和关闭功率放大器和低噪声放大器支路。“关断”支路的输入阻抗被设计为尽可能高，以最小化“导通”支路的负载，但未对发射和接收工作模式下PALNA匹配网络的损耗进行详细分析。在[10]中，采用功率放大器的负载牵引分析来设计PALNA匹配网络，以在发射时最大化输出功率，但在接收时，虽然最大化了“关断”状态PA支路的隔离度，却未对由此产生的损耗及其对噪声系数的影响进行详细分析。在[11]中，PALNA匹配网络设计实现了低噪声放大器噪声系数和功率放大器输出功率的最佳阻抗匹配，但该PALNA基于已匹配至50 Ω的PA和LNA，且未分析50 Ω匹配网络对整体PALNA损耗的贡献。在[12]和[13]中，针对低噪声放大器和功率放大器均追求最佳阻抗匹配网络设计，但未提供在发射和接收模式下匹配网络损耗及设计权衡的详细分析。

在[14]和[15]中，提出了类似于无开关PALNA的收发电路架构（见图1(d)）。在[14]中，连接PA和天线处LNA的匹配网络被设计成使得“关断”状态下的PA支路呈现为开路，且该匹配网络经过优化以有利于LNA的噪声系数性能。在[15]中，探索了一种基于变压器的隔离网络设计方法。然而，在[14]和[15]中并未给出PALNA匹配网络在发射和接收时损耗的详细分析。

本文重点研究图1(d)所示的无开关PALNA收发电路架构。提出了一种考虑损耗的PALNA匹配网络设计方法，该方法可为低噪声放大器（LNA）和功率放大器（PA）提供最优匹配阻抗。将“关断”支路（即偏置关闭的支路）作为“导通”支路的阻抗匹配枝节，并在两种工作模式下对匹配网络的损耗进行精细管理。LNA输入匹配网络和PA输出匹配网络被集成到PALNA中，并与采用50 Ω match的基于开关的收发电路相比，探讨了所能达到的最佳性能。

本文提出的PALNA电路设计方法在第二节中进行了描述。第三节介绍了适用于执行迭代式PALNA协同设计流程的低噪声放大器和功率放大器核心电路设计。第四节描述了在32纳米绝缘体上硅CMOS（32SOI）技术中无开关PALNA匹配网络的设计与实现。所讨论的迭代优化过程整合了上述LNA和PA电路设计，确保PALNA匹配网络同时为LNA提供最佳输入阻抗匹配，并为PA提供最佳输出阻抗，且损耗最小。第五节给出了32SOI PALNA电路的仿真结果，包括对PALNA电路损耗的讨论，第六节为结论。

II. PALNA电路设计方法

A. 问题描述

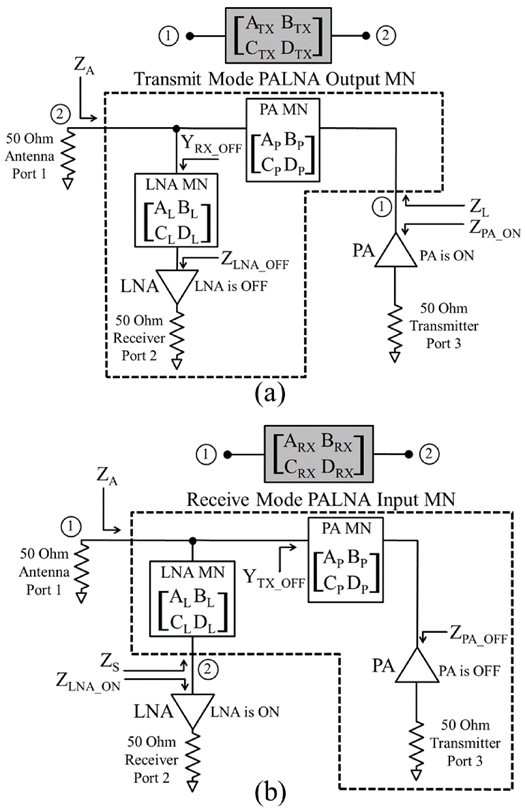
图2分别展示了所提出的PALNA电路在发射和接收模式下的原理图。本文考虑的无开关PALNA设计问题涉及无源功率放大器和低噪声放大器匹配网络的收发协同设计，使得50 Ω天线阻抗在LNA输入端和PA输出端分别被变换为最优的ZS=Zopt_LNA和ZL=Zopt_PA阻抗。假设LNA和PA不会同时开启或关闭；相反，在接收工作模式下，LNA开启而PA关闭；在发射工作模式下，PA开启而LNA关闭。所考虑的PA和LNA匹配网络包括各种阶数的传输线和集总元件LC网络。

除了在功率放大器（PA）和低噪声放大器（LNA）处实现最佳阻抗外，良好的PALNA性能还要求如图2所示的发射和接收PALNA匹配网络具有最小的换能器损耗。PALNA匹配网络中的任何损耗都会直接导致发射模式下的功率附加效率（PAE）和接收模式下的噪声系数（NF）恶化。因此，协同设计流程的一个并行任务是使用电磁仿真元件对候选匹配网络相关的实现损耗进行真实评估和管理。应选择在接收和发射工作模式下均引入最小损耗的网络作为最终方案。此外，还需考虑其他实际因素。

B. 方法论

实际的匹配网络引入了两种类型的损耗，一种是由于能量反射引起的（失配损耗），另一种是由于能量耗散引起的（耗散损耗）[16]。为了捕捉PALNA匹配网络中存在的所有损耗，对电路有源端口之间网络在发射和接收工作模式下的换能器损耗进行了仿真。为了全面表征传输线、晶体管嵌入网络以及片上集总元件中由于有限电导率和介质损耗引起的损耗，各个组件均采用电磁仿真S参数模型。

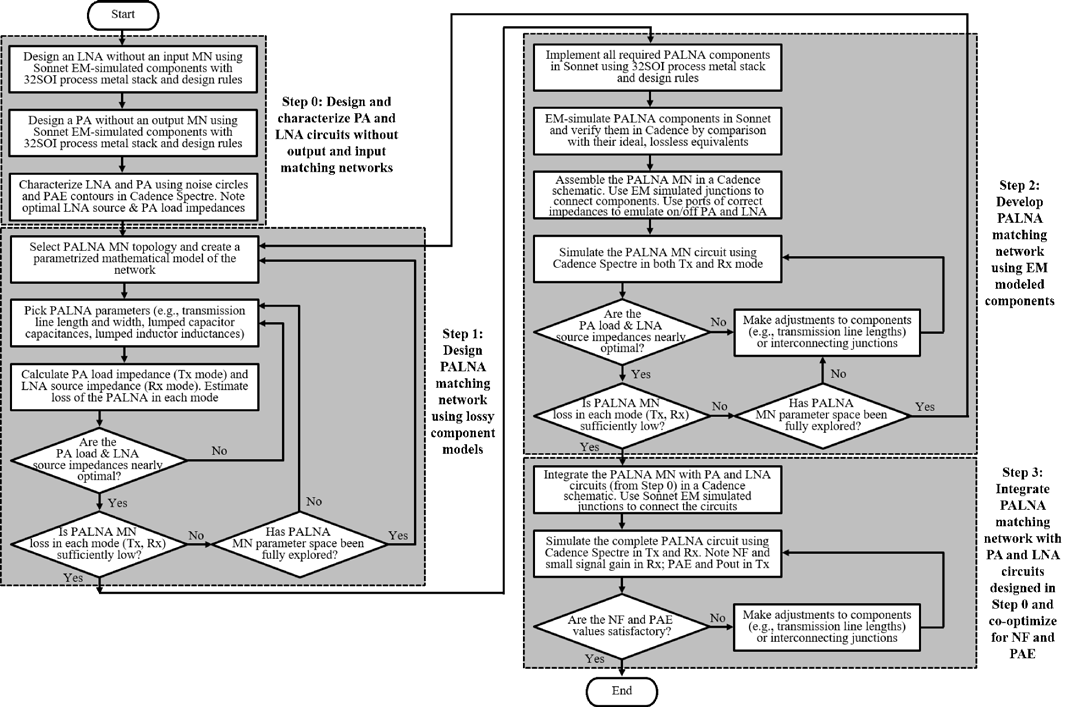
图3展示了PALNA匹配网络的逐步设计流程。

步骤0 ：设计流程首先设计不含50 Ω输出和输入匹配网络的LNA和PA核心电路。核心电路中使用的所有传输线、集总元件以及晶体管端口嵌入网络，均在Sonnet电磁(EM)仿真器中采用精确的32SOI版图几何结构进行设计和建模。核心电路中的所有晶体管均包含版图后提取的寄生参数。在完成核心LNA和PA电路的设计后，通过实验和仿真确定其导通状态、关断状态以及最佳阻抗，并通过以下三个基本的迭代步骤设计PALNA匹配网络。

步骤1 ：设计能够同时实现最佳PA和LNA阻抗的匹配网络的初始版本。在发射模式下，最佳PA负载阻抗定义为能够最大化PAE并产生良好的输出功率和功率增益的阻抗。在接收模式下，最佳LNA源阻抗定义为能够最小化噪声系数并产生良好的小信号增益的阻抗。针对每个网络，估算其在接收和发射工作模式下的换能器损耗，并选择在两种模式下损耗均最低的候选网络。传输线和集总元件分别通过衰减常数和等效串联电阻（ESR）进行有损建模，这些参数来源于Sonnet电磁仿真。

在图2a所示的PALNA发射模式中，可以将双端口网络定义为PALNA输出匹配网络与天线的级联，其中输入端口（即端口1）定义在功率放大器处，朝向PALNA输出匹配网络；输出端口（即端口2）定义在天线处，朝向外侧。可以证明，该双端口网络的[ABCD]矩阵为：

$$
\begin{bmatrix}
A_{ANT} & B_{ANT} \
C_{ANT} & D_{ANT}
\end{bmatrix}
=
\begin{bmatrix}
1 & 50 \Omega \
Y_{ANT} & Y_{RX_OFF}
\end{bmatrix}
$$

其中 $Y_{ANT}$ 是天线端口的导纳，$Y_{RX_OFF}$ 是“关闭”状态的低噪声放大器支路的导纳，其等于：

$$
Y_{RX_OFF} = \frac{C_L Z_{LNA_OFF} + D_L}{A_L Z_{LNA_OFF} + B_L}
$$

在图2b所示的PALNA接收模式中，可以将一个双端口网络定义为天线与PALNA输入匹配网络（MN）的级联，其中输入端口（即端口1）位于天线处并朝向PALNA输入匹配网络，输出端口（即端口2）位于低噪声放大器（LNA）处并朝向LNA。可以证明，该双端口网络的[ABCD]矩阵为：

$$
\begin{bmatrix}
A_{RT} & B_{RT} \
C_{RT} & D_{RT}
\end{bmatrix}
=
\begin{bmatrix}
C_L & A_L \
Y_{ANT} & Y_{TX_OFF} \
D_L & B_L \
Y_{ANT} & Y_{TX_OFF}
\end{bmatrix}
$$

其中 $Y_{TX_OFF}$ 是“关闭”状态的功率放大器支路的导纳，其等于：

$$
Y_{TX_OFF} = \frac{C_P Z_{PA_OFF} + D_P}{A_P Z_{PA_OFF} + B_P}
$$

然后，利用双端口Z参数，PALNA输入阻抗及其相关的PALNA阻抗匹配准则可以表示如下：

$$
Z_{L} = Z_{11_TT} = \frac{A_{TT}}{C_{TT}} = Z_{opt_PA}
$$

and

$$
Z_{S} = Z_{22_RT} = \frac{D_{RT}}{C_{RT}} = Z_{opt_LNA}
$$

除了上述的阻抗匹配之外，PALNA在每种工作模式下还必须具有最小的换能器损耗。利用kQ乘积的概念[17]，可以预测双端口网络功率传输效率的理论上限。给定(1)和(3)中的[ABCD]矩阵，并假设 $Y_{ANT}= 0$，可通过双端口Z参数转换表达式方便地计算PALNA的Z参数。

$$
\begin{bmatrix}
Z_{11} & Z_{12} \
Z_{21} & Z_{22}
\end{bmatrix}
=
\frac{1}{AD - BC}
\begin{bmatrix}
R_{11} & R_{12} \
R_{21} & R_{22}
\end{bmatrix}
+
j
\begin{bmatrix}
X_{11} & X_{12} \
X_{21} & X_{22}
\end{bmatrix}
$$

where $AD – BC$，因为PALNA匹配网络是互易的。由于在每种工作模式下，PALNA的Z矩阵等于

$$
kQ = \frac{|Z_{21}|}{\sqrt{R_{11} R_{22} - R_{12} R_{21}}} = \tan^2\theta
$$

then

$$
\eta_{max} = (\tan\theta)^2
$$

量化了PALNA的最大可用功率传输效率[17]。以功率传输损耗表示，该网络引起的最小损耗预期为

$$
L_{min} = 10 \log_{10}(\eta_{max})
$$

为了实现较低的耗散损耗，具有最大 $\eta_{max}$ 的PALNA电路备受关注，这可以通过在两种工作模式下针对kQ优化PALNA来实现。例如，由于 $\eta_{max}$ 是kQ的单调递增函数，且较高的kQ对应于更高的$\eta_{max}$，因此kQ为20时将导致 $\eta_{max}> 90%$，如果能够实现，则相当于可达到的最小PALNA损耗为0.43 dB。

如上所述，除了由(11)描述的耗散损耗外，PALNA网络在每种工作模式下都会在天线端口和开启放大器端口产生共轭失配损耗。这些损耗可以使用表达式[16]计算

$$
M = 10 \log_{10} \left( \frac{|Z_G + Z_1|^2}{4R_G R_1} \right)
$$

每种工作模式下的耗散损耗和失配损耗可利用换能器损耗[18]的概念方便地合并为一个整体的损耗指标

$$
L_{total} = 10 \log_{10}(L_{total})
= 10 \log_{10} \left( \frac{1}{G_{total}} \right)
$$

其中

$$
G_{total} = \frac{|S_{21}|^2(1-|\Gamma_S|^2)(1-|\Gamma_L|^2)}{|1-\Gamma_S \Gamma_m|^2 |1-S_{22} \Gamma_{21}|^2}
= \frac{4R_G R_L}{|Z_{22}+Z_L)(Z_G)|^2}
$$

公式(5)、(6)和(13)利用PA和LNA MN的[ABCD]变量表示PALNA电路的设计准则。选择特定的MN电路拓扑（例如传输线、集总元件LC电路）可将MN的[ABCD]值表示为MN电路元件值（例如传输线长度和宽度、电感、电容）的函数。为了确定在两种工作模式下均能满足设计准则的候选PALNA MN，必须求解一个多变量设计与优化问题。在本文中，针对每个候选PALNA MN及其优化变量（即电路元件值），通过计算机自动穷举搜索求解该问题，在MATLAB嵌套循环中实现了由公式(5)、(6)和(13)定义的四个目标函数（发射阻抗匹配、发射损耗、接收阻抗匹配和接收损耗），并在一定范围内的优化变量取值上进行评估，直至得到少数几组满足要求的变量集合。

设计准则。变量扫描的取值范围代表了在32SOI中实际可获得的元件值所定义的约束。

基于MATLAB的优化便于实现且操作简单，能够充分探索多种匹配网络拓扑的电路参数设计空间。另一方面，若在电路设计工具（例如本工作中的Cadence）中用手动优化替代基于MATLAB的优化，则匹配网络的设计过程将需要大量试错，且匹配网络的性能结果具有不确定性。

步骤2 ：为了进一步改进耗散损耗模型，使用格罗方德32SOI电磁仿真传输线和集总元件S参数模型，在Cadence中实现并仿真候选匹配网络。特别关注了传输线所需的长度和宽度以及整体匹配网络布局的物理尺寸等实际考虑因素。

步骤3 ：从实现角度来看，性能良好且被认为实用的匹配网络将与功率放大器和低噪声放大器电路集成，并使用Cadence Spectre进行小信号和负载牵引仿真，手动进行协同优化。协同优化过程包括在发射和接收两种工作模式之间手动切换，仿真相关性能指标，并手动调整匹配网络设计以精细优化每种模式下的性能。具体而言，在发射模式下，利用PAE负载牵引等高线、输入功率与输出功率曲线、功率增益曲线以及PAE曲线来优化性能；在接收模式下，利用噪声圆、噪声系数（NF）和小信号S参数来优化性能。所调整的匹配网络参数包括传输线尺寸和电容器的大小。

III. 32SOI中的低噪声放大器与功率放大器核心设计

A. 低噪声放大器核心设计

最近，在集成低噪声放大器设计中发现，最佳晶体管尺寸选择能够同时实现噪声与阻抗输入匹配，从而大大缓解传统的低噪声放大器设计折衷问题[19]。在本PALNA设计中，遵循了[19]中提出的低噪声放大器设计方法，并对低噪声放大器电路进行了优化，以实现最佳的噪声系数和小信号增益性能。

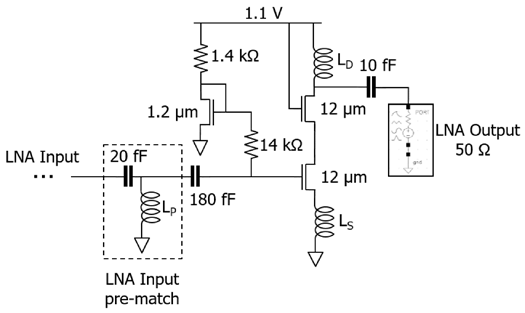
图4展示了核心94 GHz低噪声放大器电路的示意图。为了便于将该电路集成到50 Ω RF前端，假设低噪声放大器输出负载阻抗为50 Ω。采用单端单级共源共栅电路结构，并使用电流镜偏置。通过迭代仿真发现，采用1 μm指状结构、总宽度为12 μm的晶体管可在实现最大低噪声放大器增益和最小噪声系数的同时，满足最小输出匹配要求，从而实现最小损耗。图5展示了低噪声放大器晶体管布局以及在低噪声放大器电路仿真中所包含的相应电磁仿真晶体管端口嵌入网络模型。

由于实现最小噪声系数或最大增益所需的晶体管偏置电流密度（IDS/W）与CMOS技术无关，因此在低噪声放大器电路中为32SOI n型场效应晶体管选择的初始电流密度为0.1 mA/μm。然后，逐渐增加电流密度，并在每次增加时对低噪声放大器的噪声系数（NF）和增益进行仿真。最终通过仿真试验确定，低噪声放大器电路中的32SOI n型场效应晶体管应偏置在0.3 mA/μm的最佳电流密度下，这与[19]中表1给出的94 GHz数值设计示例一致。偏置电路采用1.2 μm的晶体管设计，以尽量降低电路的功耗开销。输入端的180飞法串联电容和输出端的10飞法串联电容为隔直电容。

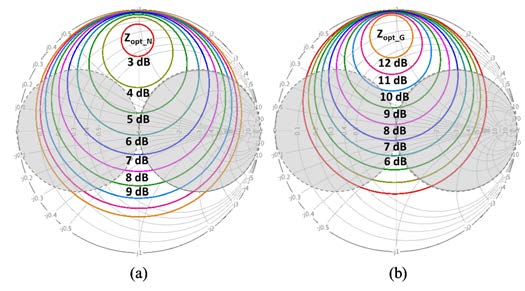
图6显示了使用Cadence Spectre仿真生成的低噪声放大器电路的恒定噪声和增益圆。

串联传输线段可用于将复数负载阻抗匹配到复数源阻抗，但这些阻抗必须位于史密斯圆图[20]上的允许区域内。在图6中，这些允许区域在每个史密斯圆图上以浅灰色表示。可以看出，为了实现最小低噪声放大器噪声系数和最大增益，低噪声放大器输入端所需的源阻抗Zopt_N和Zopt_G位于允许区域之外。这意味着在此特定情况下以及一般情况下，除非在核心低噪声放大器电路中添加“LNA输入预匹配电路”，否则低噪声放大器匹配网络（MN）不能仅由单段传输线构成，以使阻抗Zopt_N和Zopt_G进入允许区域[20]。

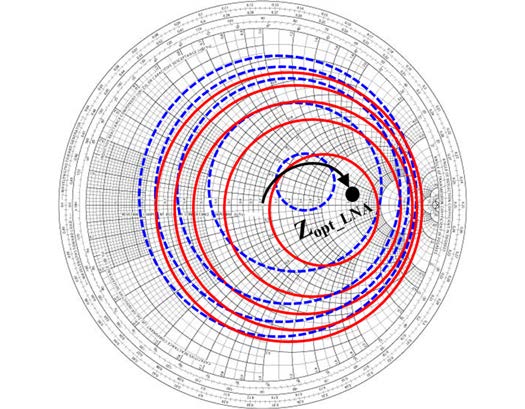
由于希望实现尽可能简单的PALNA解决方案，因此期望PA和LNA的匹配网络可能采用串联传输线。因此，在采用迭代PALNA设计流程之前，需要在LNA输入端添加“LNA输入预匹配电路”，对LNA进行“预匹配”。该预匹配通过一个L型网络实现，该网络由一个串联集总20飞法电容和一个使用传输线段实现的并联电感组成。如图7所示，在完成预匹配后，LNA的最佳源阻抗移动至史密斯圆图中的允许区域，满足设计需求。从这一点开始，PALNA匹配网络的目标是在PALNA接收模式下，将50 Ω天线阻抗变换为LNA处的最佳源阻抗Zopt_LNA，同时实现最小LNA噪声系数和最大LNA小信号增益。本文所述仿真中涉及的所有传输线、集总元件以及晶体管嵌入网络，均基于其精确的32SOI版图几何结构在Sonnet电磁(EM)仿真器中进行设计和建模。所有晶体管均包含布局后提取的寄生参数。

B. 功率放大器核心设计

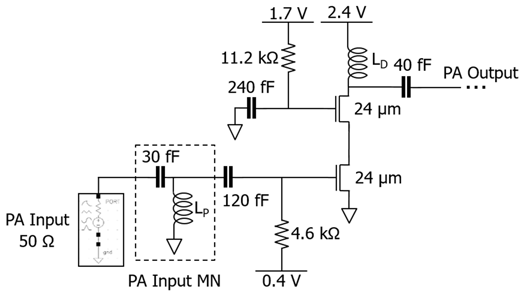
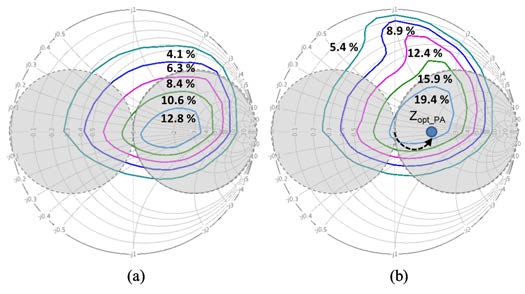
集成功率放大器设计涉及多种方法和技术，旨在管理输出功率、功率附加效率、线性度和工作带宽之间的权衡[21]。在本PALNA设计中，主要目标是最大化功率附加效率。为此，选择了采用两个堆叠器件的“类E类”功率放大器电路拓扑[22]。图8展示了核心94 GHz功率放大器电路的原理图。为了便于将该电路集成到50 Ω RF前端，假设功率放大器输入源阻抗为50 Ω。为了在94 GHz下实现最大功率附加效率以及良好的输出功率和功率增益，通过迭代仿真选用了具有1 μm根指状结构、总宽度为24 μm的nFET晶体管。图9显示了Cadence Spectre仿真结果，包括有和没有输入匹配网络时的恒定功率附加效率负载牵引等高线。这些等高线定义了在94 GHz下实现最大功率附加效率所需的功率放大器输出负载阻抗。加入输入匹配网络后，最高功率附加效率等高线的价值提升了6.6%。值得注意的是，功率放大器的最佳输出负载阻抗Zopt_PA位于史密斯圆图[20]上的允许区域内，因此除了串联的40 fF直流隔离电容外，功率放大器输出端无需额外的预匹配。PALNA匹配网络的目标将50 Ω天线阻抗变换为功率放大器处的最佳负载阻抗Zopt_PA，并在PALNA发射模式下实现最大功率放大器PAE。

第四节 PALNA在32SOI中的设计与实现

在设计完核心功率放大器和低噪声放大器电路后，在第三节中，包括图4和图8所示的所有组件，其在94 GHz下的导通/关断/最佳阻抗均来自Cadence仿真。每个电路的导通和关断阻抗通过单端口S参数仿真获得，作为复数Z11参数，分别对应电路在导通和关断状态下的偏置条件。表I总结了上述功率放大器和低噪声放大器核心电路的仿真阻抗值。

如上文第二节所述，接下来采用三步法完成PALNA电路设计。

A. 步骤1

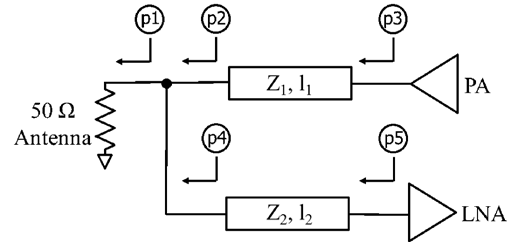
图10显示了一个PALNA网络拓扑，其中功率放大器匹配网络（PA MN）和低噪声放大器匹配网络（LNA MN）采用传输线实现。通过使用MATLAB的迭代设计流程，完成以下四项任务，以确定Z1, Z2, l1, l2,的值，从而生成满足设计准则的PALNA设计。

(1) 首先创建图10所示网络的参数化数学模型。由于功率放大器匹配网络（PA MN）和低噪声放大器匹配网络（LNA MN）是使用传输线实现的，因此每个匹配网络（MN）均用以下[ABCD]矩阵表示：

$$
\begin{bmatrix}
A & B \
C & D
\end{bmatrix}_{TL}
=
\begin{bmatrix}
\cosh(\gamma l) & Z_0 \sinh(\gamma l) \
\frac{1}{Z_0} \sinh(\gamma l) & \cosh(\gamma l)
\end{bmatrix}
$$

其中 $Z_0$ 和 $l$ 分别为传输线的特性阻抗和长度，$\gamma = \alpha + j\beta$ 为传输线复传播常数，其衰减常数 $\alpha$ 表示传输线单位长度耗散损耗，相位常数 $\beta$ 表示传输线单位长度相移。$\alpha$ 和 $\beta$ 通过Cadence仿真获得，所用S参数文件来自Sonnet中对传输线段进行电磁仿真得到的结果。

本文设计所采用的32SOI工艺是一种12层金属铝铜工艺。为了最大化传输线的品质因数Q，使用顶部四层金属（LB‐MB‐MA‐E1）将传输线实现为微带线结构，其中LB层作为信号层，E1层作为接地层。在LB与E1之间的金属层上不使用任何金属或通孔，这些中间层均填充介质材料。图11显示了在94 GHz下基于32SOI工艺设计的传输线的衰减常数随特性阻抗的变化情况。利用(1) ‐ (4)和(15)，完成了给定网络拓扑的参数模型。待求的未知网络参量为Z1, Z2, l1, 和 l2, ，其最优值通过自动搜索与优化过程获得。

所描述的网络参数模型被编码到一个MATLAB程序中。该程序包含一个四层迭代循环，对应参数Z1, Z2, l1, 和 l2, ，在其所有实际可实现的取值范围内进行扫描。每次执行循环时，针对一组特定的参数值，在循环内部计算后续步骤中所述的参量。

(2) 假设电路处于发射状态，且低噪声放大器偏置已关闭（给定低噪声放大器关断状态阻抗），在p3点（图10）计算ZL ，并与(5)中所示的Zopt_PA进行比较。发射时网络的最小换能器损耗使用(13)计算。

(3) 假设电路处于接收状态且功率放大器偏置关闭时（给定PA关断状态阻抗），在点p5（图10）计算ZS ，并与(6)中所示的Zopt_LNA进行比较。使用(13)计算网络的换能器损耗。

(4) 最小偏差范围相对于最佳阻抗的偏离程度由用户定义，如设计准则(5)和(6)中所述。如果计算得到的阻抗ZL和ZS均在此范围内，则将网络参数和性能指标存储到数据文件中以供后续审查。当循环内的代码执行完成后，更新网络参数，并重复执行任务2和任务3。该循环持续运行，直到所有Z1, 、Z2, 、l1, 和 l2的组合都被考虑完毕。当循环执行结束时，对数据文件中存储的候选解进行损耗性能和实现适用性的审查。

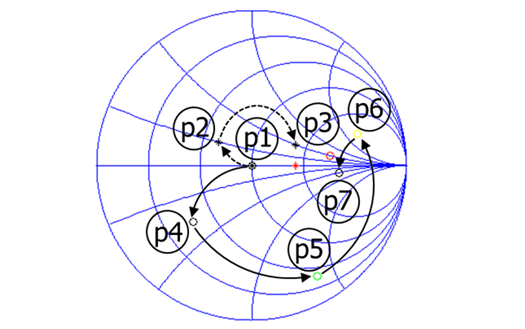
对于图10所示的网络拓扑，以下参数组合达到了最佳解决方案：Z1=38 Ω、Z2=30 Ω、l1=223 o和l2,=132 o。达到的最小换能器发射损耗和接收损耗分别为5.16分贝和4.19分贝。图12显示了PALNA在两种工作模式下的阻抗匹配性能。

需要注意的是，尽管图10中的网络拓扑能够实现良好的同时阻抗匹配在两种电路工作模式下，该拓扑结构实现的kQ均被限制在7。为了提高kQ并同时满足阻抗匹配和损耗设计准则，考虑采用具有更多自由度的PALNA拓扑结构。图13显示了一种PALNA网络拓扑，其中LNA MN使用集总元件CLC电路实现。LNA MN [ABCD]矩阵可表示为矩阵乘积

$$
\begin{bmatrix}
A & B \
C & D
\end{bmatrix}_{LNA MA 1} = M11 M22 M33
$$

其中

$$
M11= \begin{bmatrix}1 & \frac{1}{j\omega C1 + R1}\ 0 & 1\end{bmatrix}, M22= \begin{bmatrix}1 & 0\ \frac{1}{j\omega L1+ R2} & 1\end{bmatrix}, M33= \begin{bmatrix}1 & \frac{1}{j\omega C2 + R3}\ 0 & 1\end{bmatrix}
$$

而电阻 $R1…R3$ 表示电抗元件的等效串联电阻。电阻值 $R1…R3$ 是通过在Sonnet中对电容器和电感器进行电磁仿真得到的S参数文件，再利用Cadence仿真实验确定的。

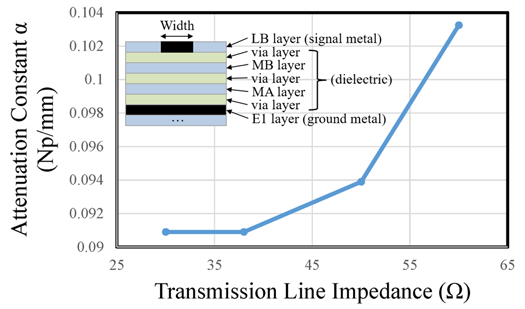
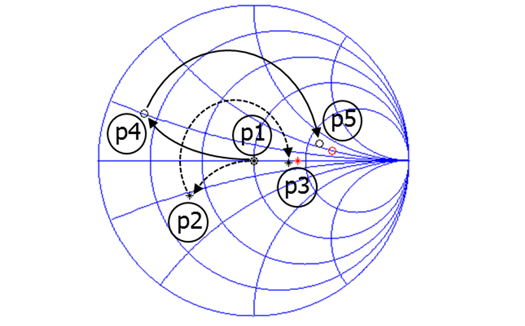
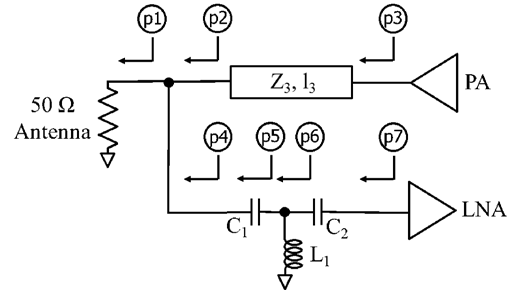
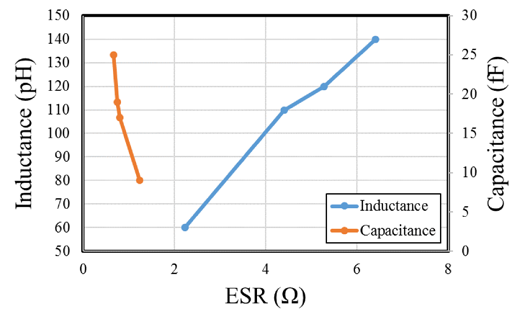
图14显示了在94 GHz下基于32SOI技术设计的电容器和电感器的等效串联电阻，分别作为电容和电感的函数。对于图13所示的网络拓扑，完成了上述四项设计任务，并针对以下参数组合获得了最佳解决方案：Z3=54 Ω，l3=122o，C1=25 fF，L1=120 pH，C2=10 fF。所实现的最小换能器发射损耗和接收损耗分别为3.58分贝和3.49分贝。

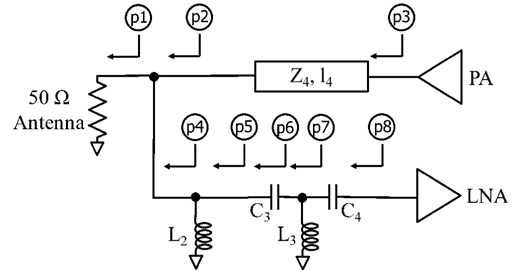
类似地，图15展示了使用集总元件LCLC电路实现LNA MN并具有额外自由度的PALNA网络拓扑。LNA MN[ABCD]矩阵可以表示为矩阵乘积

$$
\begin{bmatrix}
A & B \
C & D
\end{bmatrix}_{LNA MA2} = M11 M22 M33 M44
$$

其中

$$
M11= \begin{bmatrix}1 & 0\ \frac{1}{j\omega L2+ R4} & 1\end{bmatrix}, M22= \begin{bmatrix}1 & \frac{1}{j\omega C3 + R5}\ 0 & 1\end{bmatrix}, M33= \begin{bmatrix}1 & 0\ \frac{1}{j\omega L3+ R6} & 1\end{bmatrix}, M44= \begin{bmatrix}1 & \frac{1}{j\omega C4 + R7}\ 0 & 1\end{bmatrix}
$$

以及电阻 $R4 …R7$ 表示集总电容器和电感器的等效串联电阻。完成上述四项设计任务后，获得最佳解的参数组合为：Z4=44 Ω，l4=115 o，L2=60 pH，C3=17 fF，L3=140 pH，C4=20 fF。换能器的最小发射损耗和接收损耗分别为2.73分贝和3.31分贝。图16显示了图13和图15中PALNA网络的阻抗匹配性能。表II总结了在MATLAB中估算的三种所示PALNA的损耗指标。

除了所示的三种PALNA电路拓扑之外，图10、图13和图15中，其他电路拓扑被研究作为潜在解决方案候选。特别是，考虑了在功率放大器匹配网络和低噪声放大器匹配网络中采用各种集总元件LC电路的拓扑结构。此外，通过进一步增加低噪声放大器匹配网络中LC电路的阶数，尝试实现进一步的性能提升。然而，对于所使用的特定低噪声放大器和功率放大器核心，图10、图13和图15所示的拓扑结构表现出最佳性能。

表I 第III节核心电路在94吉赫下的阻抗
LNA输入
功率放大器输出

| 表II 三种PALNA拓扑的估计的损耗指标。换能器损耗使用 (13)计算 |
| — |
| | | 图10 PALNA | | 图13 PALNA | | 图15 PALNA |
| | Tx | Rx | Tx | Rx | Tx | Rx |
| kQ | 5.38 | 6.87 | 8.2 | 4.5 | 10.93 | 3.22 |
| 耗散损耗 [分贝] | 1.6 | 1.26 | 1.1 | 1.9 | 0.79 | 2.66 |
| 失配损耗在有源放大器 [分贝] | 1.71 | 0.15 | 1.57 | 0.19 | 1.18 | 0.28 |
| 端口处的失配损耗天线端口 [分贝] | 1.62 | 1.49 | 0.73 | 0.68 | 0.25 | 0.26 |
| 换能器损耗 [分贝] | 5.16 | 4.19 | 3.58 | 3.4
| 表III MATLAB中所需优化嵌套循环执行次数 数量 |
| — |
| 执行 | 图10 PALNA | 图13 PALNA | 图15 PALNA |
| 执行 | 361,890* | 2,082,730* | 782,994* |
(*) 执行运行时间在标准商用笔记本电脑

表 IV 实现电路所需的传输线 FROM STEP 1 组件
传输线
传输线
传输线
传输线
电感器
电感器
电感器

B. 步骤2

首先，在Sonnet中实现了上述PALNA电路所需的所有组件的电磁模型，包括具有预期布局几何结构的完整传输线。Sonnet模型中使用了精确的32SOI技术金属堆叠结构。传输线和电感器被实现为微带线，电容器则被实现为金属‐氧化物‐金属（MOM）结构。通过仿真对电感器和电容器的确切几何形状进行优化，调整其几何特征，直到其仿真性能与所需理想元件的性能最接近为止。对于电感器，调整微带线宽度和长度；对于电容器，则调整重叠金属板的尺寸以及重叠量。表IV列出了在图10、图13和图15中实现所需组件的尺寸。

在32SOI中，采用图11的微带结构。在Sonnet中生成各组件的电磁S参数模型后，将其集成到图10、图13和图15的Cadence Spectre电路原理图中，以替代相应的传输线、电容器和电感器。功率放大器（PA）和低噪声放大器（LNA）核心电路被替换为具有适当开/关复阻抗的端口，如上表I所示，并使用Cadence Spectre进行小信号仿真。根据PALNA设计准则，在每种PALNA网络的每种工作模式下记录两个参量，即网络呈现给有源放大器的阻抗，以及网络在天线与有源放大器端口之间引入的换能器损耗。

表V 步骤1中三个PALNA的Cadence仿真结果
Mode
Tx
Tx
Tx
Rx
Rx
Rx

表VI 94 GHz下PALNA损耗汇总
工作模式 操作
Tx
Rx

共轭
共轭

由于换能器损耗会直接导致PALNA在噪声系数（NF）和功率附加效率（PAE）方面的性能下降，而对整个PALNA电路在Cadence Spectre中进行噪声圆和负载牵引仿真非常耗时，因此这是一种设计PALNA电路的有效、高效且必要的方法。鉴于抽象化的PALNA仿真运行速度非常快，设计者可以进行大量优化迭代，可在不同工作模式之间切换，调整电路，并同时协同设计PALNA，直至两种模式下的设计准则均得到满足。

表V总结了图10、图13和图15所示的三种PALNA网络在Cadence实现中的仿真结果。从表中可以看出，参考图7和图9，这三种网络均能为PA和LNA提供可接受的阻抗匹配。然而，图15所示的网络在两种工作模式下引入的换能器损耗最小。

此外，通过调整PALNA匹配网络以适应不同程度的换能器发射或接收损耗，这种协同设计方法使得设计PALNA匹配网络成为可能，从而在发射端性能与接收端性能之间进行权衡。这对于特定应用设计具有潜在价值，例如在某些噪声系数（NF）性能可以牺牲以提升整体功率附加效率（PAE）性能的收发器电路中。传统的50 Ω匹配的基于开关的收发电路不具备这种灵活性，因为开关在两种工作模式下引入的损耗通常大致相等。

根据表V所示的仿真性能，图10和图13所示的网络被舍弃，而选择图15所示的网络进行下文的进一步研究。此外，图10所示的网络需要相对较长且较宽的传输线，导致最终的收发器电路在物理尺寸上较大，这从实现角度来看是不理想的。

接下来，将组件结的电磁S参数模型添加到选定的PALNA电路原理图中，并通过迭代过程重新调整PALNA传输线的长度，以重新优化PALNA的性能。表VI总结了从Cadence仿真中获得的最终PALNA电路的相关损耗。仿真得到的PALNA匹配网络的最大功率传输效率为在发射和接收工作模式下的效率分别为81%和51%。这些效率决定了PALNA匹配网络本身所消耗的最小功率量，且独立于天线以及功率放大器/低噪声放大器电路的阻抗匹配条件。如表VI第1列所示，这些效率对应于PALNA匹配网络在发射和接收模式下的最小理论损耗分别为0.9分贝和2.9分贝。

除了PALNA匹配网络本身引起的最小损耗外，由于天线以及各个放大器电路处的共轭阻抗失配，还会产生额外的损耗。这些损耗如表VI所示，可通过考察图2来进一步理解。具体而言，PALNA匹配网络损耗是指在发射或接收模式下，在天线端口与功率放大器输出端或低噪声放大器输入端之间测得的换能器损耗。共轭天线失配损耗是在天线处测得的，由ZA与50 Ω天线之间的阻抗失配引起。共轭放大器失配损耗则在每个开启状态的放大器处测得；对于功率放大器，该损耗由ZOUT_PA与ZL之间的阻抗失配引起，而对于低噪声放大器，则由ZIN_LNA与ZS之间的失配引起。

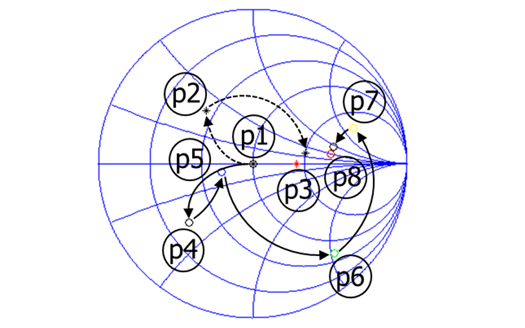
需要注意的是，表VI中总结的损耗值与上述表II中给出的结果非常吻合。图17显示了最终PALNA匹配网络的Cadence仿真阻抗匹配结果。PAE负载牵引等高线（代表发射模式下的匹配目标）叠加在噪声圆（代表接收模式下的匹配目标）之上。红色圆点表示实现的发射模式阻抗，蓝点表示实现的接收模式阻抗。两种模式下均实现了良好的匹配。需要注意的是，出于清晰考虑未显示低噪声放大器增益圆，但最大增益得以实现，且噪声系数的劣化最小。

C. 第3步

在最终设计步骤中，完整的PALNA电路在Cadence中实现，并进行了一系列完整的仿真，包括小信号S参数、增益圆、噪声圆、稳定性、恒定功率附加效率负载牵引轮廓以及大信号仿真。这是PALNA电路设计的关键最后一步，考虑了所有电路变量和损耗。在Cadence仿真中，手动切换发射和接收模式，并手动调整PALNA电路的参数，直到两种模式下均获得满意性能。在发射模式下，PALNA针对PAE、输出功率和功率增益进行优化；在接收模式下，PALNA针对小信号增益和噪声系数进行优化，同时保持稳定性。优化过程还额外考虑了LNA和PA的最大电流和电压额定值，以确保其鲁棒性（例如，在PA处于发射状态时检查LNA输入端的峰值电流和电压幅值）。

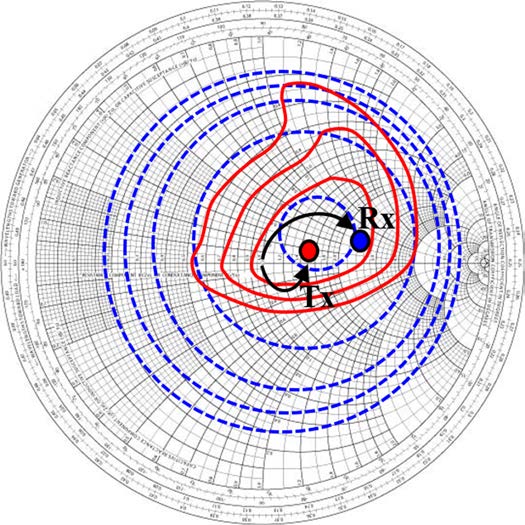
图18显示了最终的94 GHz PALNA电路设计原理图。完成该电路设计所需的手动设计迭代次数少于10次。第五节包含PALNA电路仿真结果的总结。

V. 32SOI PALNA 在 94 GHz 下的仿真结果

最终PALNA电路设计的仿真性能如图19–23所示。

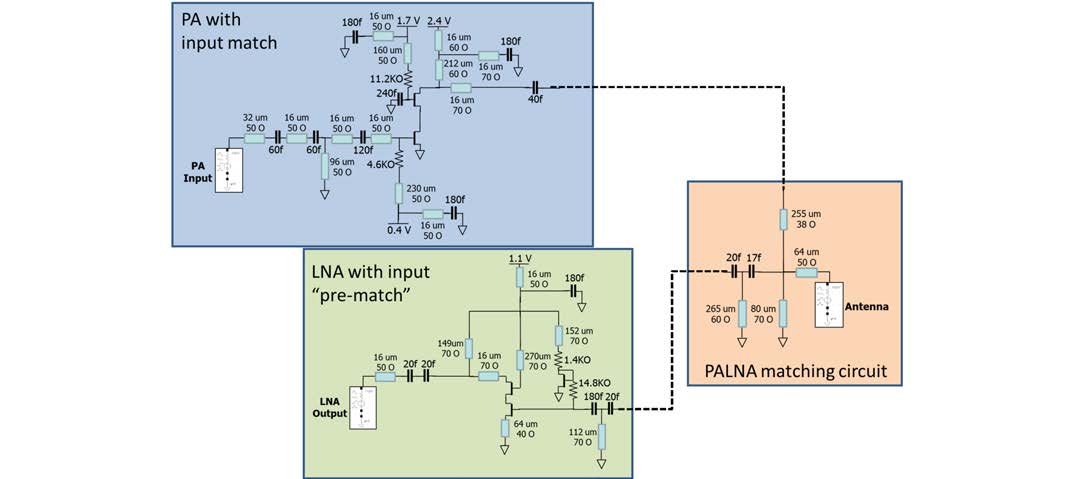
图19显示了PALNA匹配网络在发射和接收模式下的仿真换能器损耗。尽管两种工作模式下均可实现3分贝的损耗，但由于主要设计目标是最大化功率附加效率，因此有意将发射模式设计为具有略低的损耗。

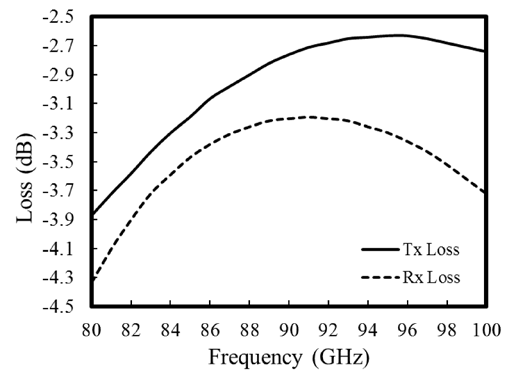
相比接收模式。图20显示了工作在接收模式下的PALNA小信号S参数和噪声系数。在94 GHz的设计频率下，s21增益为8 dB，电路稳定。噪声系数为7.5 dB，考虑到LNA核心电路的最小仿真噪声系数以及PALNA匹配网络的3.3 dB损耗，该结果符合预期。

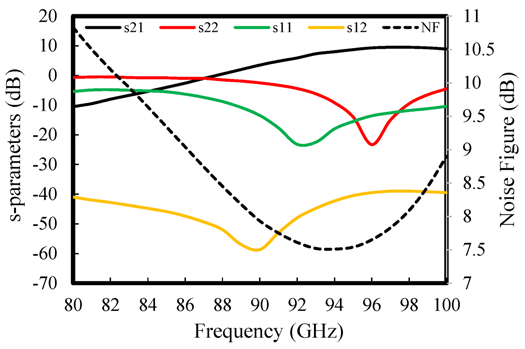
图21显示了PALNA在发射工作模式下的仿真大信号输出功率、功率增益和功率附加效率。图22显示了PALNA大信号性能随工作频率的变化情况。图23显示了PALNA端口隔离度随频率的仿真结果。在94 GHz时，发射和接收端口隔离度分别为18.7 dB和>20 dB。这些隔离结果与在94 GHz下集成收发开关所能实现的隔离性能相当[1]。根据瞬态仿真结果，PALNA电路的模式切换速率可达4 GHz，预计足以满足大多数关注应用的需求。

表VII PALNA性能比较
频率 [GHz]
最大功率增益 [dB]
最大PAE [%]
饱和功率 [分贝毫瓦]
接收增益 [dB]
噪声系数 [分贝]

基于开关的 T/R,
(*) 仿真基于实测的2.2分贝单刀双掷损耗。

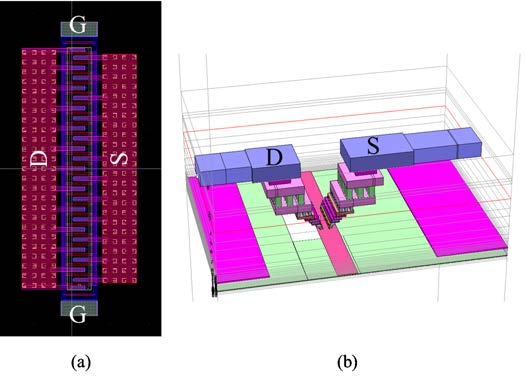
表VII展示了无开关PALNA电路与两种可比的最先进（SoA）电路以及一种传统的基于开关的收发电路之间的仿真性能比较，其中基于开关的收发电路来自[1]，并使用了与无开关PALNA电路相同的功率放大器（PA）和低噪声放大器（LNA）电路。基于开关的收发电路和无开关PALNA的性能均通过Cadence Spectre进行仿真。在基于开关的收发电路中，功率放大器（PA）和低噪声放大器（LNA）分别在其输出端和输入端具有50 Ω匹配网络，因为该开关具有50 Ω个端子。基于开关的收发电路中的每条信号路径被独立仿真，并通过在每条路径[1]中插入一个50 Ω、2.2分贝的电阻衰减器来近似估算收发（T/R）开关的损耗。PALNA避免了在天线端口使用50 Ω匹配网络，在发射性能上优于基于开关的收发电路，即使PALNA在发射时的损耗为2.6分贝，高于开关2.2分贝的损耗。

另一方面，基于开关的收发电路在所需的芯片布局面积上比无开关PALNA电路大40%，这是一个显著的劣势。

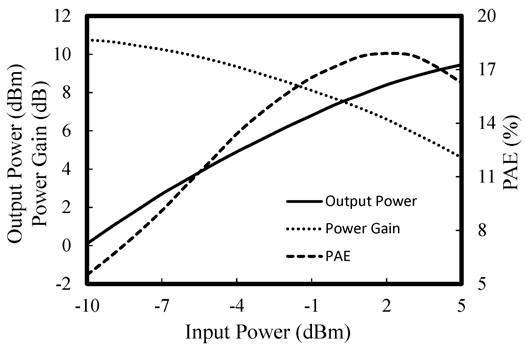
图24a显示了无开关PALNA电路的布局，图24b显示了相应的基于开关的收发电路的布局。

在设计方法中未明确考虑PALNA带宽，而是从图20和图22的结果中推断得出，并认为其对于目标系统应用已足够。具体而言，1分贝噪声系数带宽为12吉赫兹，范围从87.5吉赫兹到99.5吉赫兹；‐5%功率附加效率带宽为9吉赫兹，范围从87吉赫兹到96吉赫兹。通过改变功率放大器MN传输线长度在其设计值附近±20%进行的设计后敏感性分析表明，1分贝噪声系数带宽在12吉赫兹的设计值上下从11吉赫兹变化到13吉赫兹。仅基于该接收模式性能，我们会倾向于将功率放大器MN传输线的长度尽可能缩短。然而，在考虑发射端性能后，我们选择了226 μm的设计长度，同时牺牲了一些低噪声放大器带宽性能。

带宽也可以正式作为目标之一纳入PALNA设计方法，但代价是增加了嵌套迭代循环。为了将带宽作为设计目标，设计者首先需要在电路工作的每种模式下定义一个带宽指标。然后，在每次迭代中，必须将带宽评估为一个或多个额外的目标函数，从而影响最终的PALNA解决方案。此外，由于线性度在所考虑的系统应用中重要性较低，因此本工作未将其用作优化目标。然而，线性度将在未来工作中予以考虑。

表VI提供了关于PALNA匹配网络损耗来源的见解，并为未来PALNA设计中的损耗降低提出了可能的途径。具体而言，未来的研究应关注以下两个方向：首先，从表VI可以看出，功率放大器共轭失配损耗为1.08 dB，而低噪声放大器共轭失配损耗仅为0.22 dB。尽管使用增益圆选择最佳低噪声放大器源阻抗可确保LNA输入共轭失配损耗较低，但最佳功率放大器负载阻抗仅针对最大功率附加效率进行选择。由于通常情况下，实现最大功率附加效率和最小共轭失配损耗所需的最佳功率放大器负载阻抗并不相同，因此未来的研究应从两个方面展开：（1）如何设计功率放大器核心，使其在最大功率附加效率和最小共轭输出失配损耗方面的输出匹配要求相一致；（2）如何选择一个能够在功率附加效率与因功率放大器输出端共轭失配损耗而引入的PALNA匹配网络损耗之间提供最有利权衡的最佳功率放大器负载阻抗。其次，应利用本文提出的针对两种工作模式的PALNA匹配网络优化方法，探索更多能够最大化功率传输效率的PALNA拓扑结构，从而最小化PALNA匹配网络自身耗散的功率。

VI. 结论

本文提出了一种考虑损耗的分析方法，用于适用于新兴毫米波相控阵的无开关PALNA收发集成电路的分析与设计。该方法是一种实用、迭代、通用的方法，用于解决开发PALNA匹配网络的多变量优化问题，使匹配网络在发射与接收工作模式下同时为功率放大器（PA）和低噪声放大器（LNA）提供最佳匹配阻抗，并最小化耗散损耗和失配损耗。该方法可应用于任意集成电路制造工艺和任意工作频率下的PALNA设计，以减小收发电路的尺寸或相较于等效的基于开关或环形器的设计提升其性能。为比较目的，在32SOI技术中设计了两款实用的94 GHz集成收发电路：一款采用单刀双掷开关的收发电路和一款无开关PALNA。基于开关的收发电路物理尺寸比无开关PALNA大~40%，而无开关PALNA在功率附加效率（PAE）等关键参数上表现出相当或更优的性能。