MLAPP————第三章离散数据的生成模型

最新推荐文章于 2025-03-03 13:22:50 发布

QQQiZZZ

最新推荐文章于 2025-03-03 13:22:50 发布

阅读量3k

点赞数 2

分类专栏： mlapp

本文链接：https://blog.youkuaiyun.com/marmove/article/details/81220495

版权

本章介绍了离散数据的生成模型，重点关注贝叶斯概念学习，包括似然、先验、后验及其在模型选择中的作用。通过数字游戏举例说明了概念学习的过程，并探讨了先验对模型的影响。此外，详细阐述了beta-二项式模型和Dirichlet-multinomial模型，展示了如何进行模型拟合和预测。最后，讨论了朴素贝叶斯分类器的模型拟合、预测和特征选择方法，以及在词袋模型下的文件分类应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

第三章离散数据的生成模型

3.1 介绍

在2.2.3.2中，讨论了通过生成分类器对特征进行分类，利用如下公式：，利用这个模型的关键就是对于每个类别指定一个合适的条件概率密度函数，这一章我们主要考虑的数据是具有离散的特征，同时我们也会考虑如何去推断模型的参数。

3.2 贝叶斯概念学习

概念学习，举个例子，一个小孩是如何学习狗这个概念的呢，一般在遇到狗时，家长会对小孩说，这是狗，所以都是从正例出发。一般来说不会说这不是狗，除非在小孩指着猫说这是狗，家长会给予指正。然而心理学家的研究表明，对于概念的学习，仅仅通过正的例子就可以了。

其实学习一个概念跟二项分类很像，就是学习一个函数f，如果输入是跟概念一致的，输出1，否则输出0.如果允许给出一些不确定性，也就是说用概率去描述，我们可以产生模糊集理论。

书中给出了一个叫数字游戏的例子。游戏是这样的，比如我选择一些数学上关于数的概念C，‘质数’，‘1到10之间的数’。我随即从这些概念中选一些数 $\mathcal D = \{x_1,\cdots,x_N\}$ 出来给你，然后我给一些测试样本 $\tilde x$ ，让你找出测试样本中哪些是属于C的，哪些不属于C。为了简单起见，数都是从1-100里面取的。我们先看下图：

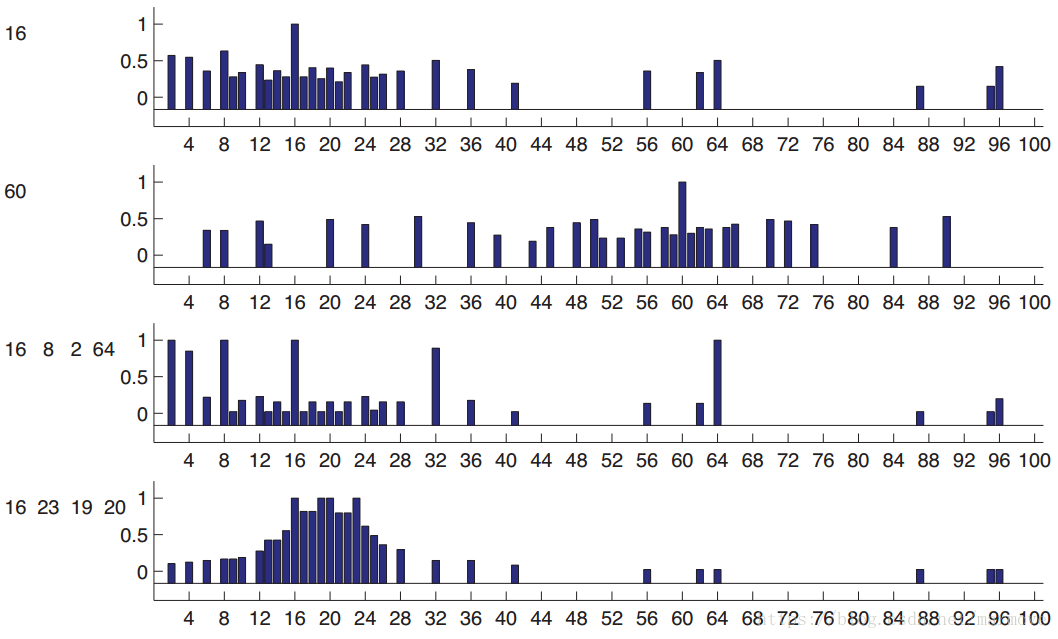
上图这个概率都是人工经验预测出来的。如果我只说16是正例，就是图的第一行，或者第二行图的60，当我只告诉你一个数的时候，预测会变得非常的模糊，对于16，17有可能，因为接近，2有可能，因为是偶数，所以很难判断。我们可以把每个数字所含有的概率表示为 $p(\tilde x|\mathcal D)$ ，这是后验预测分布（posterior predictive distribution）。现在我们假设，16，8，2，64是正例的话，那么就对应于第三行的图。那么这个时候你可能大概率觉得这个概念就是2的指数次方。如果我说16，23，19，20是正例，那么你可能就觉得这个概念就是20左右的数字，这对应着图的第四行。那么在实际计算机仿真当中我们该怎么做。首先我们需要一个假设空间 $\mathcal H$ （hypothesis），在这里可以表示为很多的概念，比如奇数，偶数等等。那么包含数据 $\mathcal D$ 的假设空间叫做版本空间（version space）。但是有个问题就是，版本空间可能有很多个，比如说对于16，偶数，平方数，都是版本空间，那么哪一个的可能性最大，我们后面就要讲到如何用贝叶斯的观点去看待和解决。

3.2.1 似然

我们必须要去解释，为什么当 $\mathcal D = \{16,8,2,64\}$ ，我们要选择‘2的指数’这个概念而不是‘偶数’这个概念。关键点就是我们要避免一些可疑的巧合，如果是偶数，那么为什么我们看到的都是2的指数呢？

我们假设从某个概念中抽取样本的时候，概率是均匀分布的。那么我们从假设h中抽取N个样本，那么概率就是：。这个就称之为似然（likelihood）。明显看出对于上面的 $\mathcal D$ ，如果h是‘2的指数’，似然为 $7.7\times10^{-4}$ ，而如果h是‘偶数‘的话，那么似然为 $1.6\times10^{-7}$ 。这里我们要强调，似然不是概率分布，积分并不等于1。

3.2.2 先验

还是用上面的例子 $\mathcal D = \{16,8,2,64\}$ ，假如有一个新的概念是‘2的指数中除了32’，就是把2的指数里面的数把32扔掉，那么明显这个概念的似然会更加的大，那么是不是这个概念更好呢？但是一个严重感觉上的问题就是这个概念太特殊了，所以说我们需要引入先验（prior）的概念。先验是很有用的，因为在很多不同的场景下，我们对一些数据的判断会不一样。针对我们之前的例子给出下图：

最左边是先验，我们看到，对于奇数和偶数因为发生的概率确实大一点，所以先验比较大，其余很多概念一样，最后类似于2的指数除去32这种概念，先验是非常小的。

3.2.3 后验

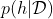后验就是先验乘以似然然后归一化：，3.2.3中的图就表示了针对数据 $\mathcal D = \{16\}$ ，先验似然后验的概率分布。当我们的数据量足够的多的时候，那么 $p(h|\mathcal D)$ 就会只在一个概念的地方呈现尖峰。所以说，这个就是delta函数。那么所以我们得到后验之后，我们通常用最大后验估计（MAP）的方法得到最终的假设。即：。我们可以看到这个和我们之前经常用的最大似然（MLE）估计：

就是差了一个先验项。我们可以明显看到，似然是与数据量有关的，当我们的数据量越来越大的时候，先验的作用就会变得越来越微弱，MAP也就会越来越接近MLE。

3.2.4 后验预测分布

后验就是我们对于我们所要预测的东西的置信状态。而后验的可靠性往往通过你对现实的结果的观察去看你的预测是否准确。

比如在刚才的数的分类当中，，这个式子的意思我觉得写得不是很清楚：其中数据是已知的，左边就是 $\tilde x$ 属于类里面的概率。右边第二项是在数据 $\mathcal D$ 下，不同假设的概率，右边的第一项就是在这个假设下， $\tilde x$ 是属于这个假设的概率（属于这个假设为1，否则为0）。这个也称之为贝叶斯模型平均（Bayes model averaging）。因为对于问题本身我们需要的是给你一个数据 $\mathcal D$ ，给你一个 $\tilde x$ ，问你 $\tilde x$ 是否是