快速卷积算法winograd原理推导

最近看到文章中说采用winograd快速卷积算法可以减少神经网络中图像卷积的乘法次数，因为之前做过cnn，当时卷积用的最简单的滑动窗口方式计算卷积，因此对这个快速卷积比较有兴趣，文章中先以一维的为例阐述了winigrad的如下思想：

其中下面的m1、m2、m3、m4的表达式是winograd的一个关键内容，通过这种转换将原本需要6次乘法减少到了4次（当然加法增加了），但是文中没有给出如何推导出的m1、m2、m3、m4的表达式，原论文中也没有，由于原论文中给出的是特殊形式，如果结果有变化类似的表达式需要自己推导，因此本人尝试了下m1、m2、m3、m4的表达式的推导的过程，大概如下：

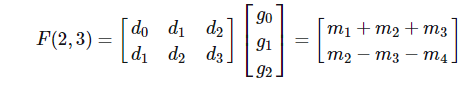
首先要做的是将上图中由d0\d1\d2\d3\g0\g1\g2的矩阵乘法转换为只用4个变量m1、m2、m3、m4表达的形式，因为输出是两个值，表达式需要有两个。m1、m2、m3、m4四个变量之间只用加减法实现，观察d0\d1\d2\d3\g0\g1\g2的矩阵乘法的形式，假设第一个表达式包含m1、m2、m3,第二个表达式包含m2、m3、m4，按照上图中的假设第一个表达式为m1+m2+m3,第二个表达式为m2-m3-m4,其中m2和m3的符号对推导有很大作用，下面以第一个表达式为m1+m2+m3、第二个表达式为m2-m3-m4的前提推导m1、m2、m3、m4的表达形式：
将上图展开后为：
d0g0+d1g1+d2g2=m1+m2+m3
d1g0+d2g1+d3g2=m2-m3-m4
从上式直观看，m1应该包含d0g0,m4应该包含d3g2,因此先假设m1=d0g0,m4=-d3g2,在次假设下代入上式，则可以约掉m1、