今天来介绍我的二叉树学习过程
二叉树的定义
首先我们需要先知道如何用指针的形式来定义一个二叉树,这对我们后续的学习相当有帮助
class treenode
{
public:
int val;
treenode *left;
treenode *right;
treenode(int x)
{
val=x;
left=nullptr;
right=nullptr;
}
};
于是我们可以将treenode当做类似结构体来运用,当我们需要定义一个根节点时,我们只需使用treenode* root就可以
前序遍历,中序遍历,后序遍历,层序遍历
接下来我们来介绍二叉树的各种遍历,我们先来画出一个二叉树
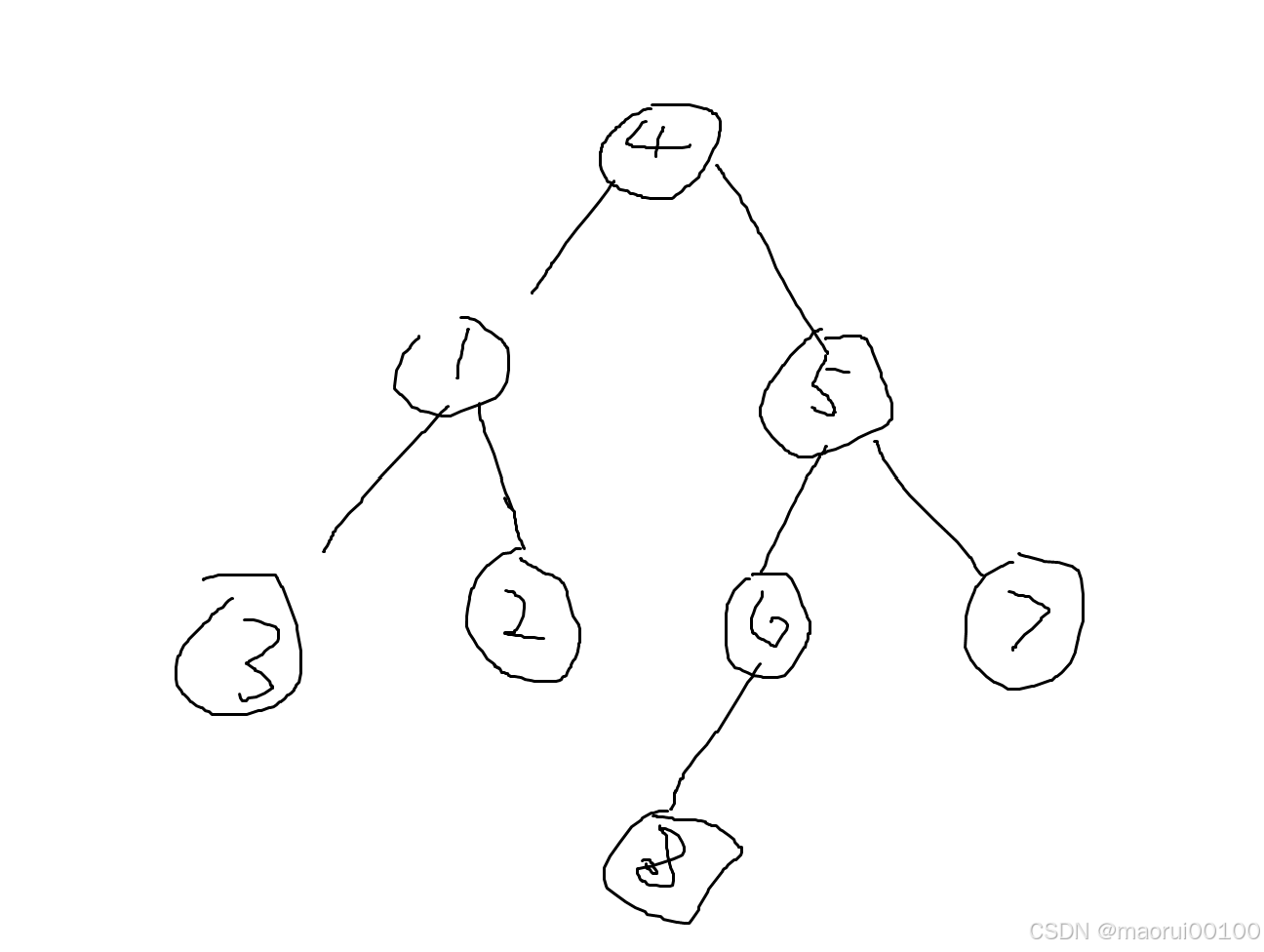
(画的有点丑)
前序遍历
前序遍历就是按照根节点,左节点,右节点的顺序来遍历整棵树
可以理解为从根节点开始,一路向左,直到实在走不了了,我们就开始往右走,我来画出一个示意图
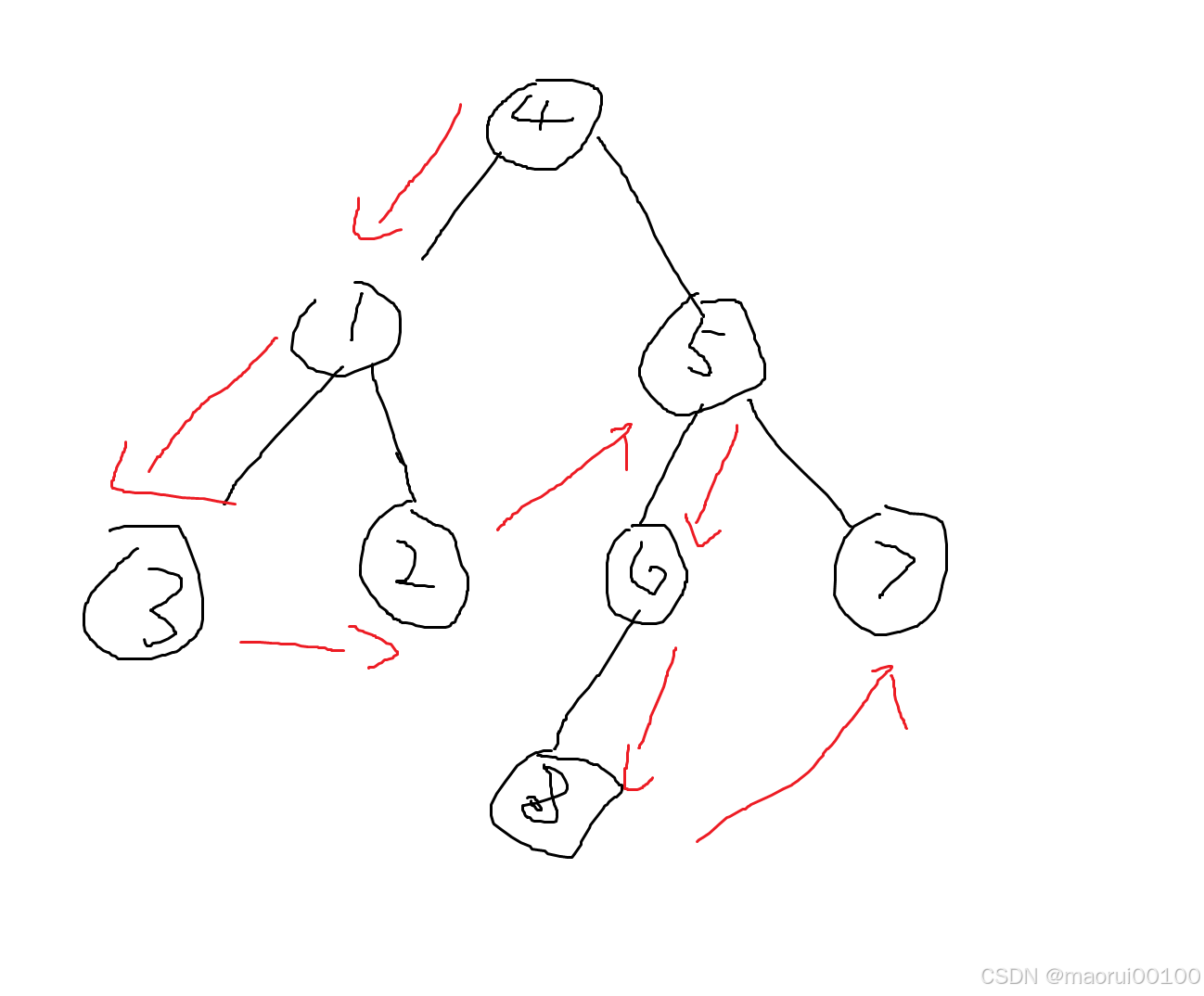
由此我们可以清楚的得到其前序遍历为4,1,3,2,5,6,8,7
中序遍历
中序遍历则是按照左节点,根节点,右节点的顺序进行遍历
可以理解为我们从最左边的叶子节点开始进行遍历,遇到有更左的节点,我们优先前去,不然则向上找根节点,最后是右节点,依旧是给出示意图
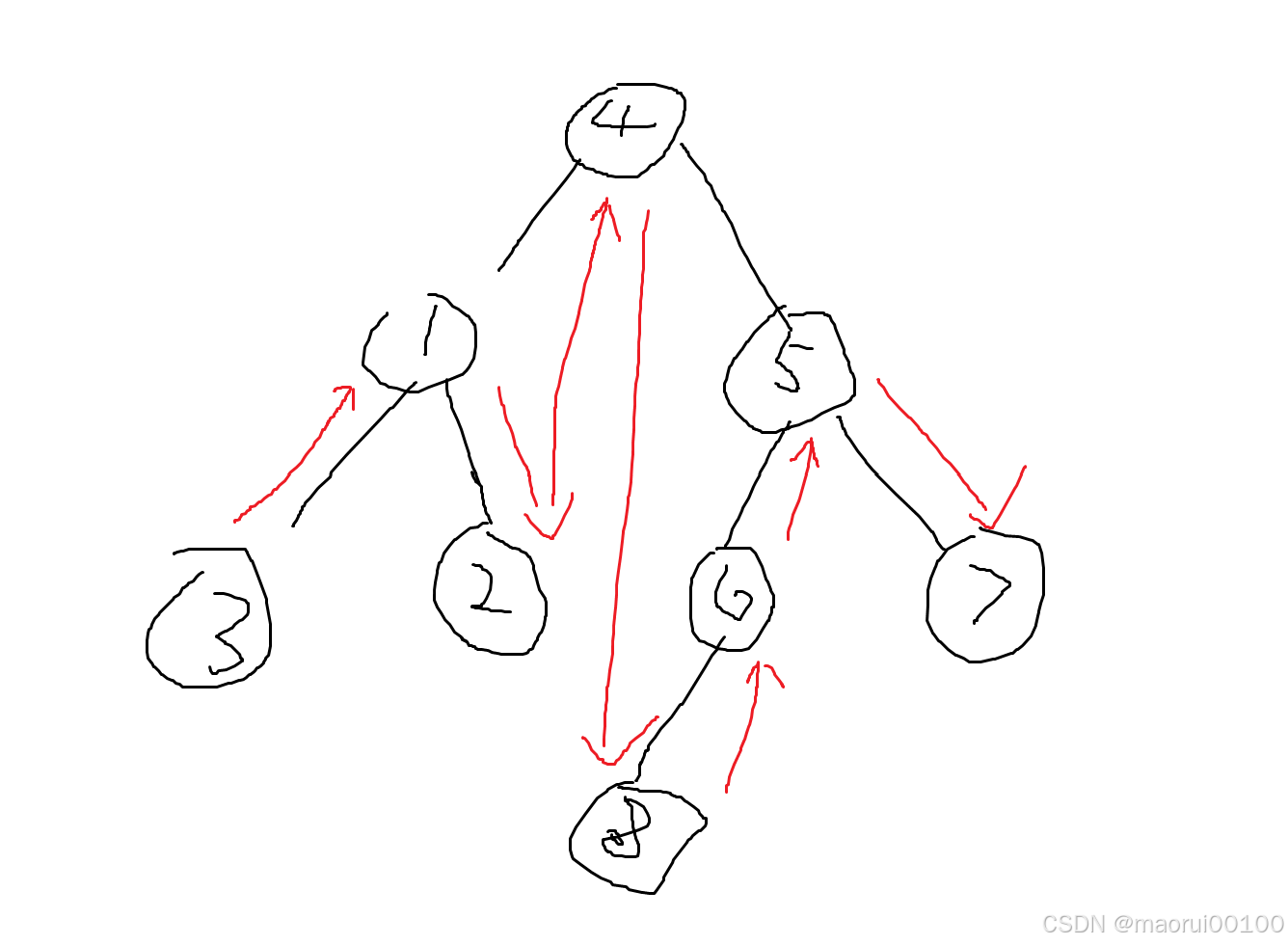
由此我们可以清楚的得到其中序遍历为3,1,2,4,8,6,5,7
后序遍历
后序遍历则是按照左节点,右节点,根节点的顺序进行遍历,这里直接给出示意图
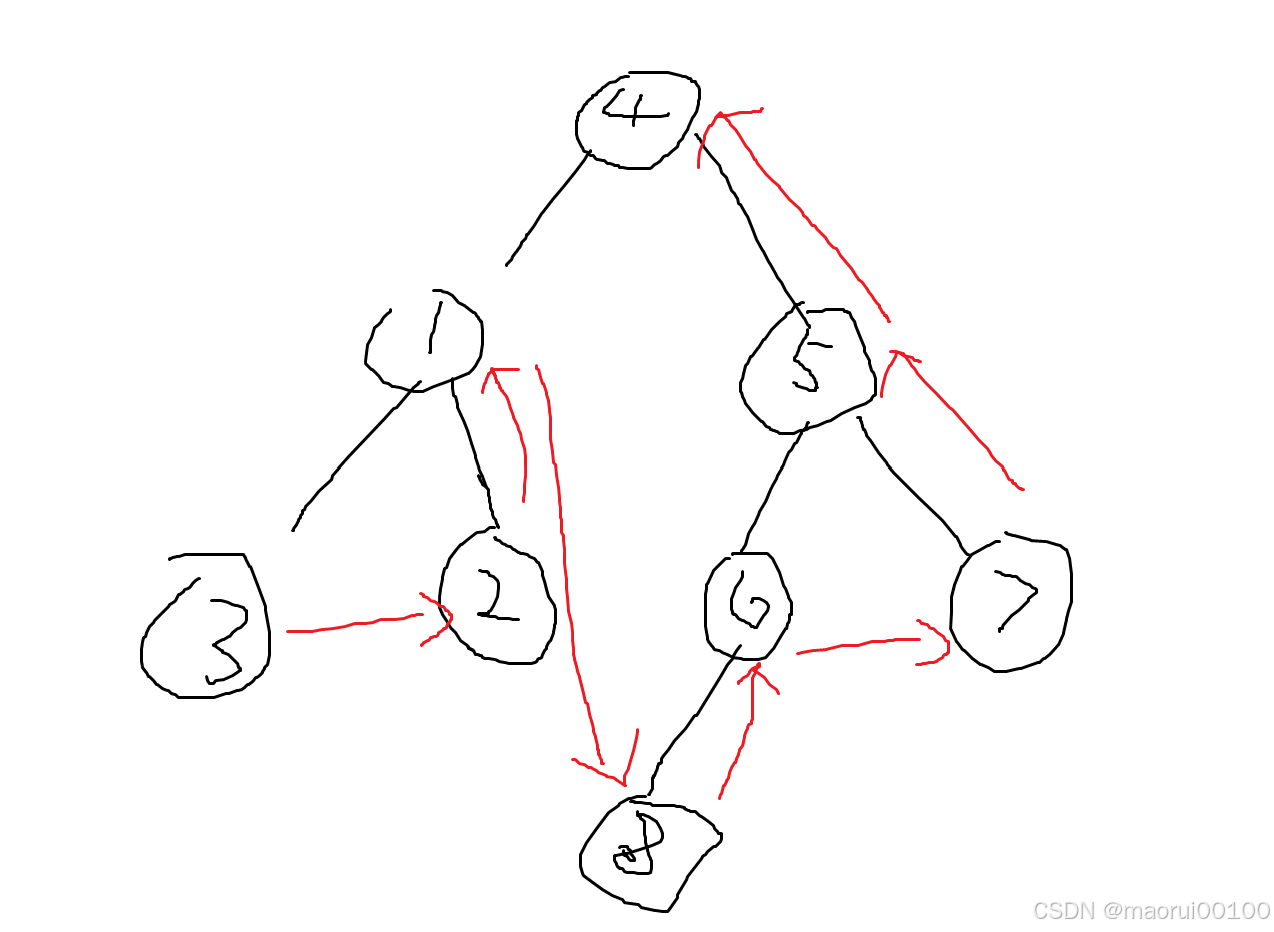
由此我们可以清楚的得到其中序遍历为3,2,1,8,6,7,5,4
层序遍历
层序遍历就很简单了,就是按照二叉树的层第几层遍历,从根节点开始,第一层,第二层,第三层依次遍历,这个的实现方法我会在后面介绍
例题
OK接下来我来介绍一个例题,来源是pta的天梯题库
给定一棵二叉树的后序遍历和中序遍历,请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
输出样例:
4 1 6 3 5 7 2
这就考察我们对于各种遍历方式的理解了
首先我们能发现,对于后序遍历,我们总能发现最后一个节点是根节点
于是我们可以在中序遍历中找到根节点,它的左边是左子树,右边是右子树,然后我们不断递归来查找即可,下给出代码
class treenode
{
public:
int val;
treenode *left;
treenode *right;
treenode(int x)
{
val=x;
left=nullptr;
right=nullptr;
}
};
int hx[35];
int zx[35];
int n;
vector<int>ans;
treenode* build(int l1,int r1,int l2,int r2)
{
if(l1>r1||l2>r2)
{
return nullptr;
}
int findroot2=hx[r2];
treenode* root=new treenode(findroot2);
int findroot1;
for(int i=l1;i<=r1;i++)
{
if(zx[i]==findroot2)
{
findroot1=i;
break;
}
}
int lefttreesize=findroot1-l1;
root->left=build(l1,findroot1,l2,l2+lefttreesize-1);
root->right=build(findroot1+1,r1,l2+lefttreesize,r2-1);
return root;
}
void cxbl(treenode* root)
{
queue<treenode*>q;
q.push(root);
while(!q.empty())
{
treenode* node=q.front();
q.pop();
ans.push_back(node->val);
if(node->left!=nullptr)
{
q.push(node->left);
}
if(node->right!=nullptr)
{
q.push(node->right);
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>hx[i];
}
for(int i=1;i<=n;i++)
{
cin>>zx[i];
}
treenode* root=build(1,n,1,n);
cxbl(root);
for(int i=0;i<ans.size();i++)
{
printf("%d",ans[i]);
if(i!=ans.size()-1)
{
printf(" ");
}
}
return 0;
}
这里的cxbl函数就是我们提到的层序遍历实现方法,我们用队列存储,保证其一定按照层序
镜像
镜像就是是指将所有非叶结点的左右孩子对换。
我们可以采取递归的方法,交换左右子树,先给出例题
给定一棵二叉树的中序遍历和前序遍历,请你先将树做个镜面反转,再输出反转后的层序遍历的序列。所谓镜面反转,是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。
输入格式:
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。
输出格式:
在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔,行首尾不得有多余空格。
输入样例:
7
1 2 3 4 5 6 7
4 1 3 2 6 5 7
输出样例:
4 6 1 7 5 3 2
下给出代码
#include<bits/stdc++.h>
using namespace std;
class treenode
{
public:
int val;
treenode *left;
treenode *right;
treenode(int x)
{
val=x;
left=nullptr;
right=nullptr;
}
};
int qx[35],zx[35];
vector<int>ans;
treenode* build(int l1,int r1,int l2,int r2)
{
if(l1>r1||l2>r2)
{
return nullptr;
}
int findroot1=qx[l2];
treenode* root=new treenode(findroot1);
int findroot2;
for(int i=l1;i<=r1;i++)
{
if(zx[i]==findroot1)
{
findroot2=i;
break;
}
}
int lefttreesize=findroot2-l1;
root->left=build(l1,findroot2,l2+1,l2+lefttreesize);
root->right=build(findroot2+1,r2,l2+lefttreesize+1,r2);
return root;
}
void mirror(treenode* root)
{
if(root==nullptr)
{
return;
}
if(root->left==nullptr&&root->right==nullptr)
{
return;
}
if(root->left!=nullptr||root->right!=nullptr)
{
treenode* temp=root->left;
root->left=root->right;
root->right=temp;
}
mirror(root->left);
mirror(root->right);
}
void cxbl(treenode* root)
{
queue<treenode*>q;
q.push(root);
while(!q.empty())
{
treenode* node=q.front();
q.pop();
ans.push_back(node->val);
if(node->left!=nullptr)
{
q.push(node->left);
}
if(node->right!=nullptr)
{
q.push(node->right);
}
}
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>zx[i];
}
for(int i=1;i<=n;i++)
{
cin>>qx[i];
}
treenode* root=build(1,n,1,n);
mirror(root);
cxbl(root);
for(int i=0;i<ans.size()-1;i++)
{
printf("%d ",ans[i]);
}
printf("%d",ans[ans.size()-1]);
return 0;
}
ok,今天就先讲到这里,相信大家对二叉树有了基本的了解




















 1558
1558

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








