线段树（单点更新以及区间更新模版）

今天来讲一下我的线段树学习历程。

线段树的模版算法，就是将所给的数据存储在一个树中，可以快速的查找一个区间内的最值或一个区间的和，并支持单点或者区间的修改。

接下来先来讲一下最基础的单点修改以及查找最值

给定一组数字，假设我们需要查找某个区间的最值。

先来画一个图

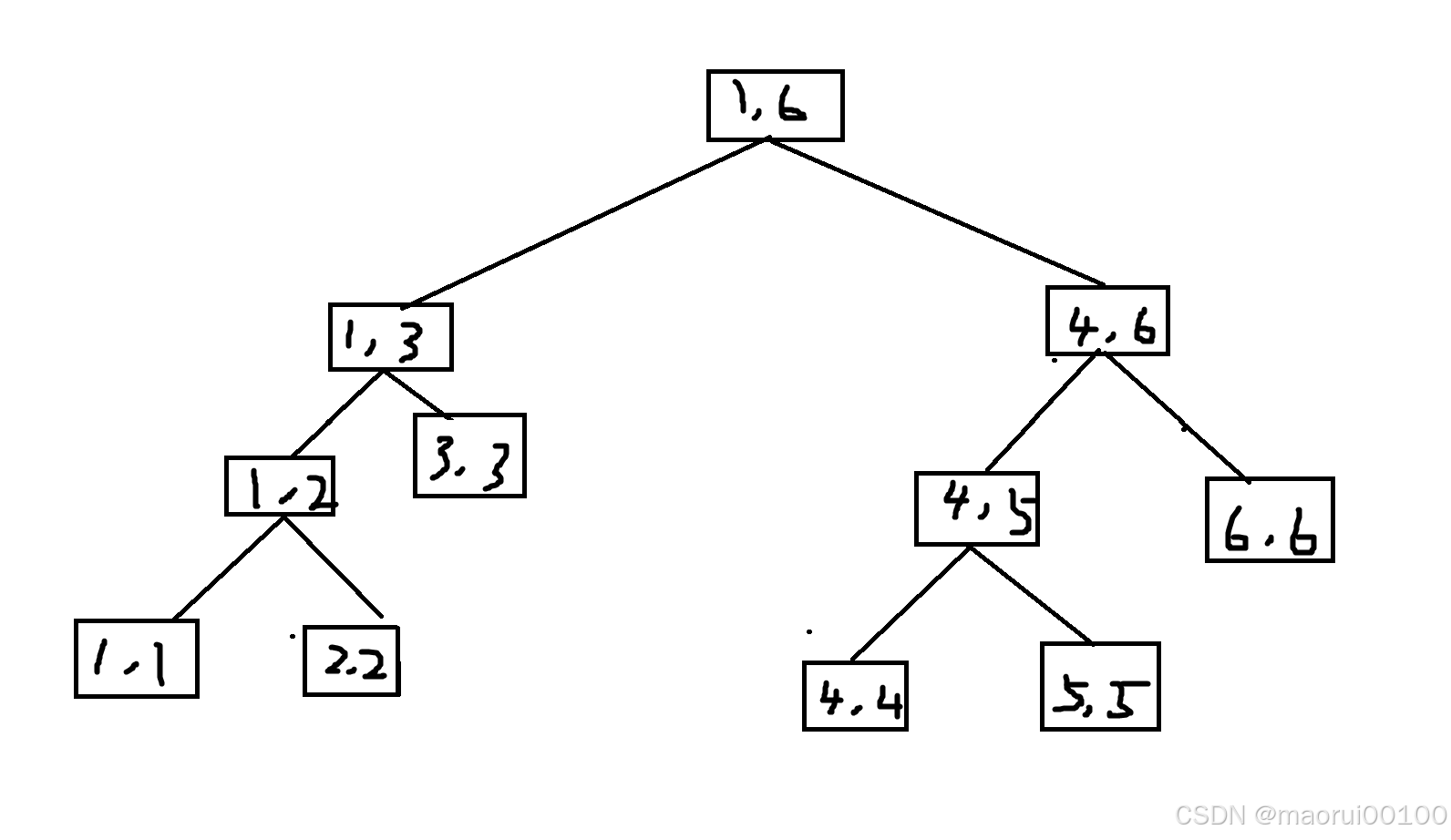
其中每个方格上的两个数字表示区间。

接下来，我们假设这六个数的值分别为1,1,4,5,1,4

那么我们用红色的数将每个区间的最值表示在旁边

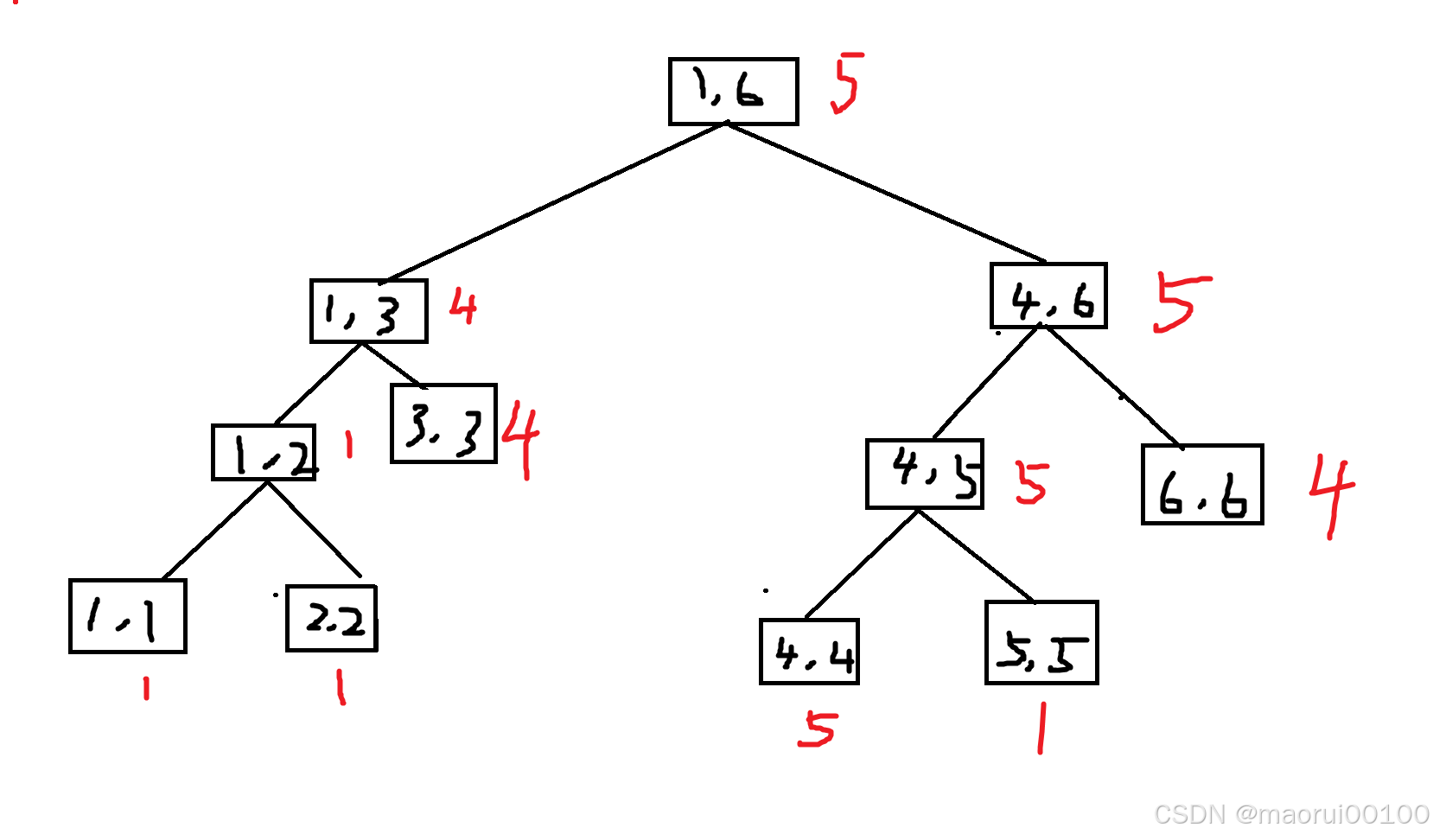 那么很显然，当我们要查询形如（4,6）的区间时，我们可以轻松得出答案。

那如果我们要查询的区间时（3,5）呢？

这时我们可以看出，（3,5）实际上是（3,3）和（4,5）的组合。

那么我们只需不断递归区间，当此时的区间被包含在查询区间内时，我们便返回这个值，并在回溯时记录最大值即可。

那么先来给出最基本的建树函数

const int maxn=1000005;
int tr[maxn];//这里用来记录每个区间节点的最值
int a[maxn];//这里用来记录n个数字，比如上图中的1,1,4,5,1,5
void build(int l,int r,int id)
{
    if(l==r)//叶子节点
    {
        tr[id]=a[l];
    }
    int mid=(l+r)/2;
    build(l,mid,id*2);//递归左儿子
    build(mid+1,r,id*2+1);//递归右儿子
    tr[id]=max(tr[id*2],tr[id*2+1));//记录最值
}

这里的id实际上是每个节点的标号。显然左儿子为id*2，右儿子为id*2+1

那么接下来，我们来查找每个区间的最值

int find(int l,int r,int x,int y,int id)
{
	if(l>=x&&r<=y)//如果被查询区间包含
	{
		return tr[id];
	}
	int ans=-1000000000;
	int mid=(l+r)/2;
	if(x<=mid)//如果x大于mid，则无需递归左区间
	{
		ans=max(ans,find(l,mid,x,y,id*2));
	}
	if(y>mid)//如果y小于mid，则无需递归右区间
	{
		ans=max(ans,find(mid+1,r,x,y,id*2+1));
	}
	return ans;
}

那么我们该如何实现单点修改呢？

假设我们将1,1,4,5,1,4改为了1,1,4,6,1,4

我们先一路找到第4个树的叶子节点，发现是（4,4），我们将tr[id]改为6

接下来，我们一路向上更新其父节点

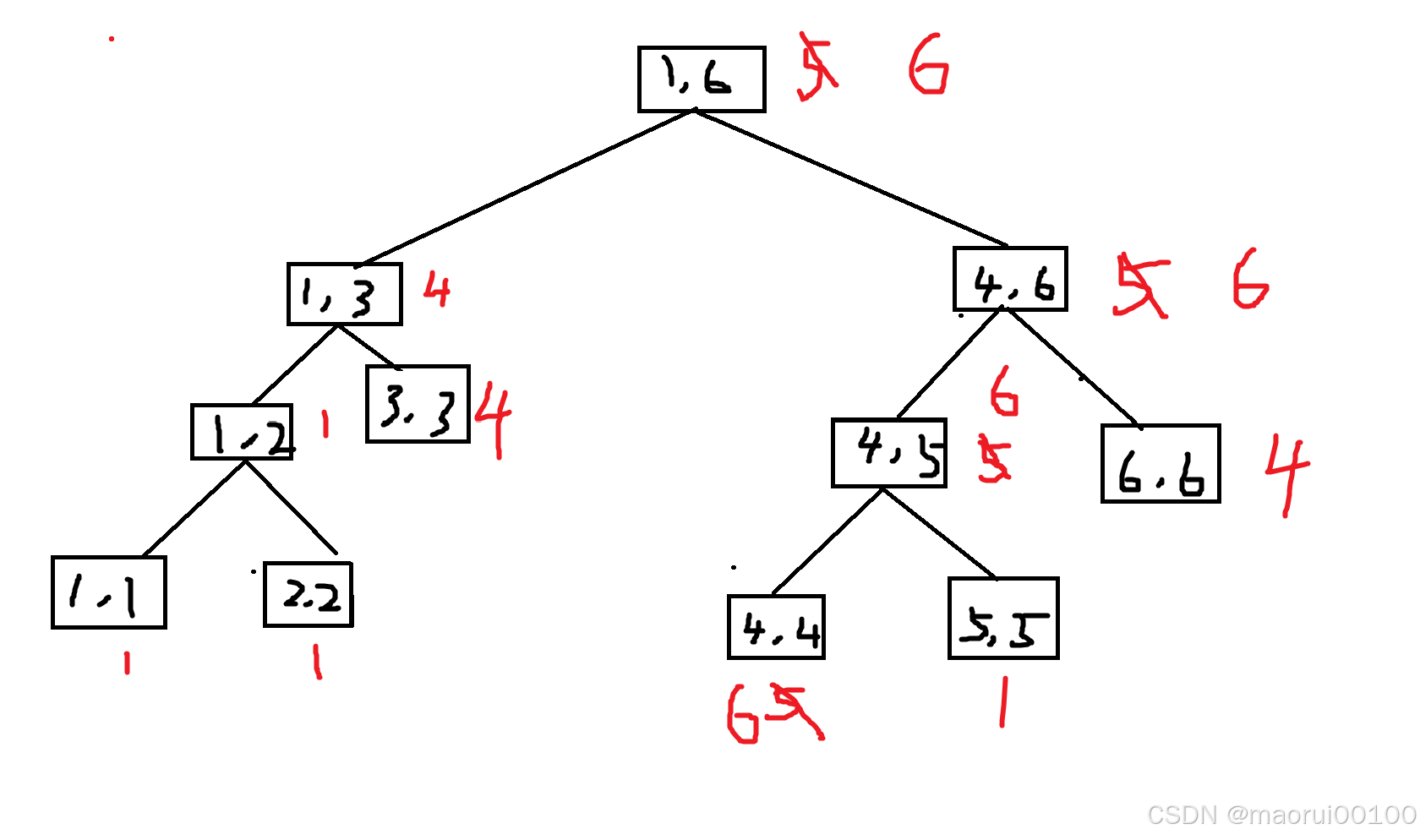
怎么样，是不是其实很简单？

void ddgx(int id,int l,int r,int x,int v)//x为要修改的点，v为被修改成的值
{
	if(l==r)
	{
		tr[id]=v;
		return;
	}
	int mid=(l+r)/2;
	if(x<=mid)//在左区间
	{
		ddgx(id*2,l,mid,x,v);
	}
	else//在右区间
	{
		ddgx(id*2+1,mid+1,r,x,v);
	}
	tr[id]=max(td[id*2],td[id*2+1]);
}

那么接下来讲一下区间更新

实际上，其实对区间的每个点单点更新也能实现区间更新，但这样显然速度太慢了

那么我们要用到的就是懒标记（lazy-tag）

其实我在网上看了很多有关懒标记的理解，但我感觉还是都太抽象了，我尽量给大家讲明白。

我们假设一个lazy[id]，他的含义是对于id这个区间，对区间加上的值。

比如一个lazy[id]表示（1,6）区间，那么显然对于sum，有sum[id]=(6-1+1)*lazy[id]

那么我们得到了第一个基本的公式sum[id]=lazy[id]*(r-l+1)

那么最基础的问题来了，为什么我们需要这个lazy？

我们来画个图理解一下

首先依旧是1,1,4,5,1,4

我们用红笔表示lazy，用蓝笔表示sum

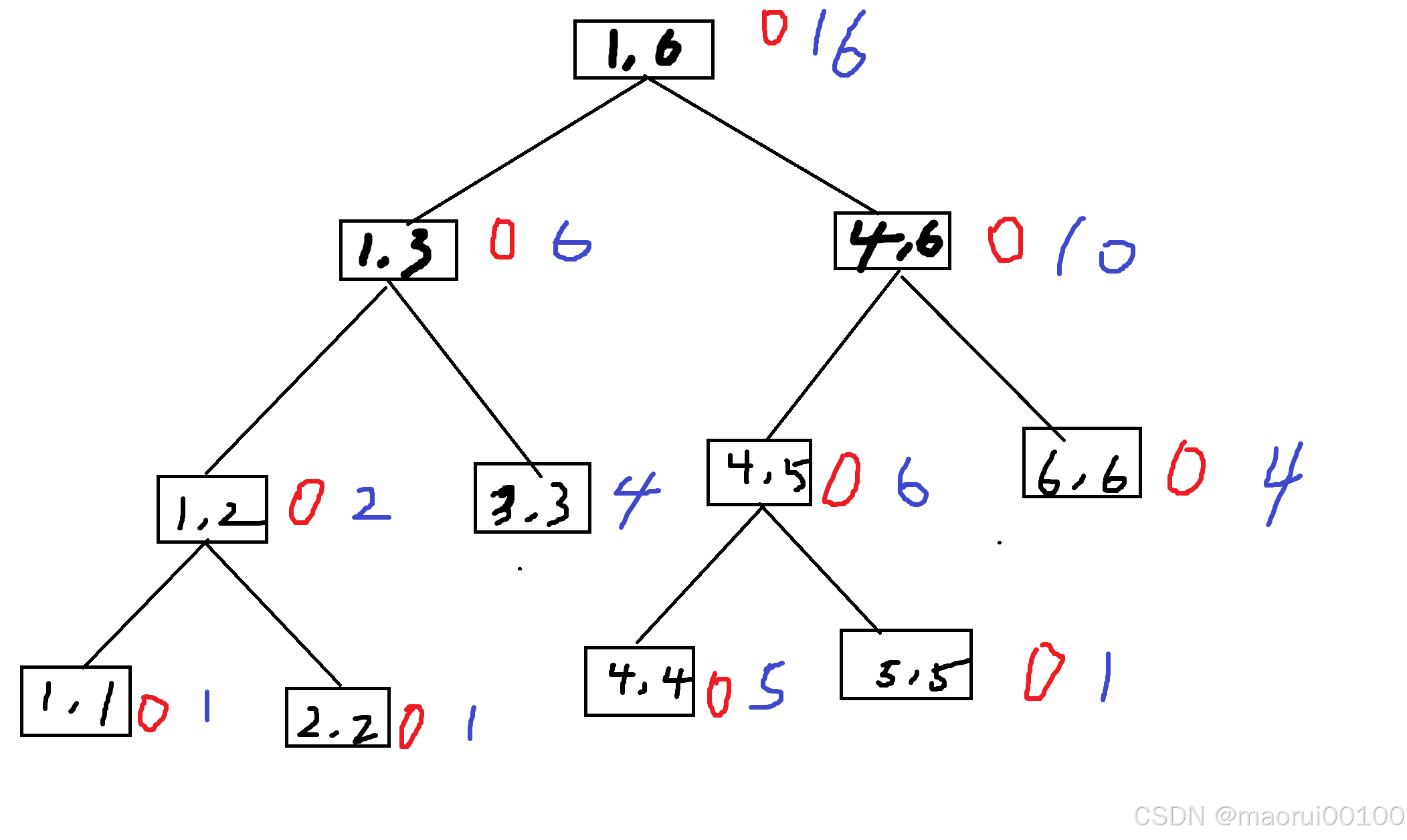
现在我们要在（1,6）区间加上1

那么显然，如果我们对每个点都处理，显然是太麻烦了

于是我们只对（1,6）进行lazy和sum的改变（因为很懒啊）

于是就变成了

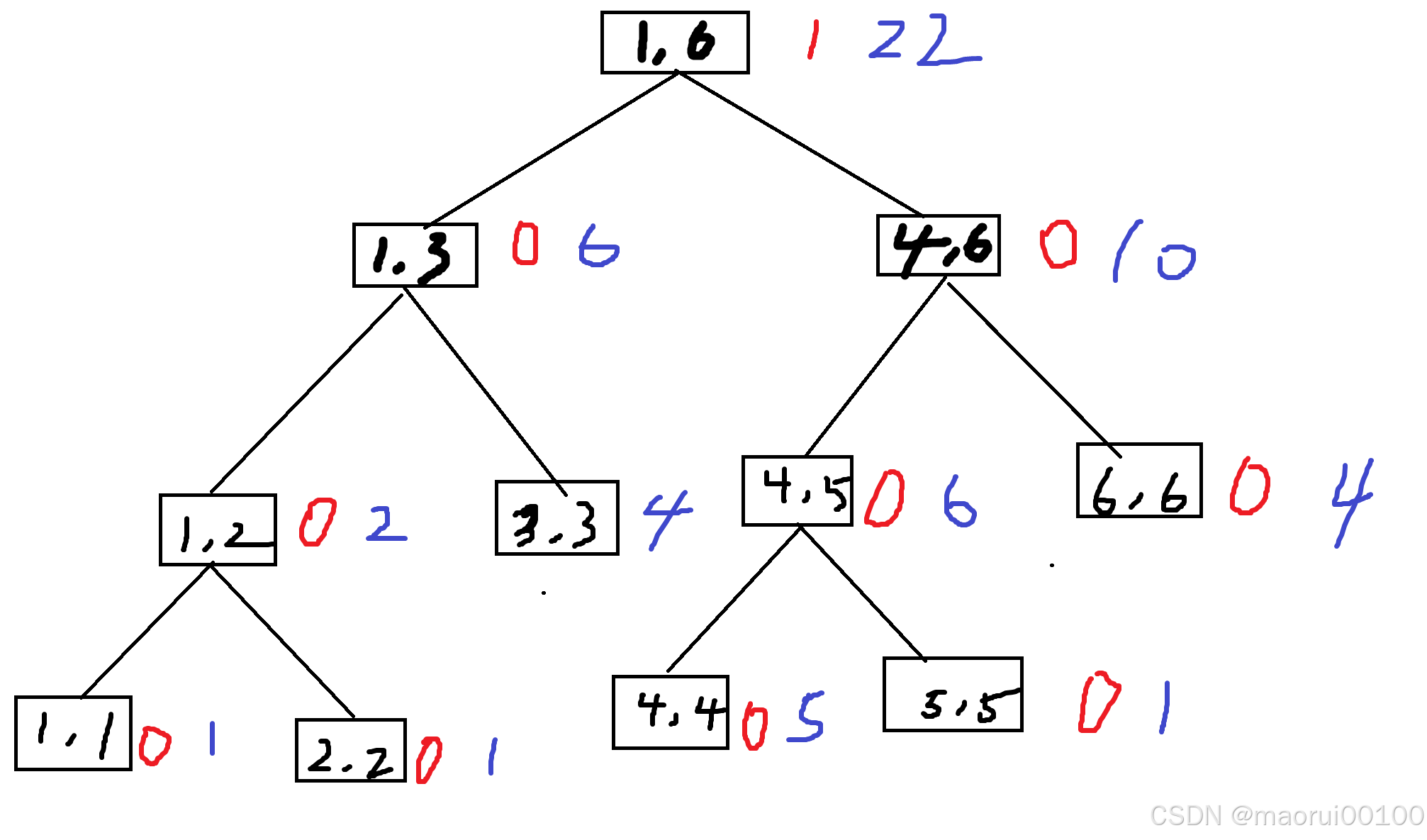
哈哈，这时就有人要问了，如果接下来我要修改（1,3）怎么办？？？

我们假设对（1,3）加2

因为我在之前没有对（1,3）进行修改，但他其实被改变了

那我们直接开始下放！！！

比如我们先查看（1,6），这时我们发现它没有包含（1,3）

于是我们将（1,6）携带的lazy进行下放

我们对（1,3）与（4,6），让他继承（1,6）的lazy

并让（1,3）和（4,6）的sum改变

这时因为（1,6）的lazy被下放了，所以将（1,6）的lazy改为0

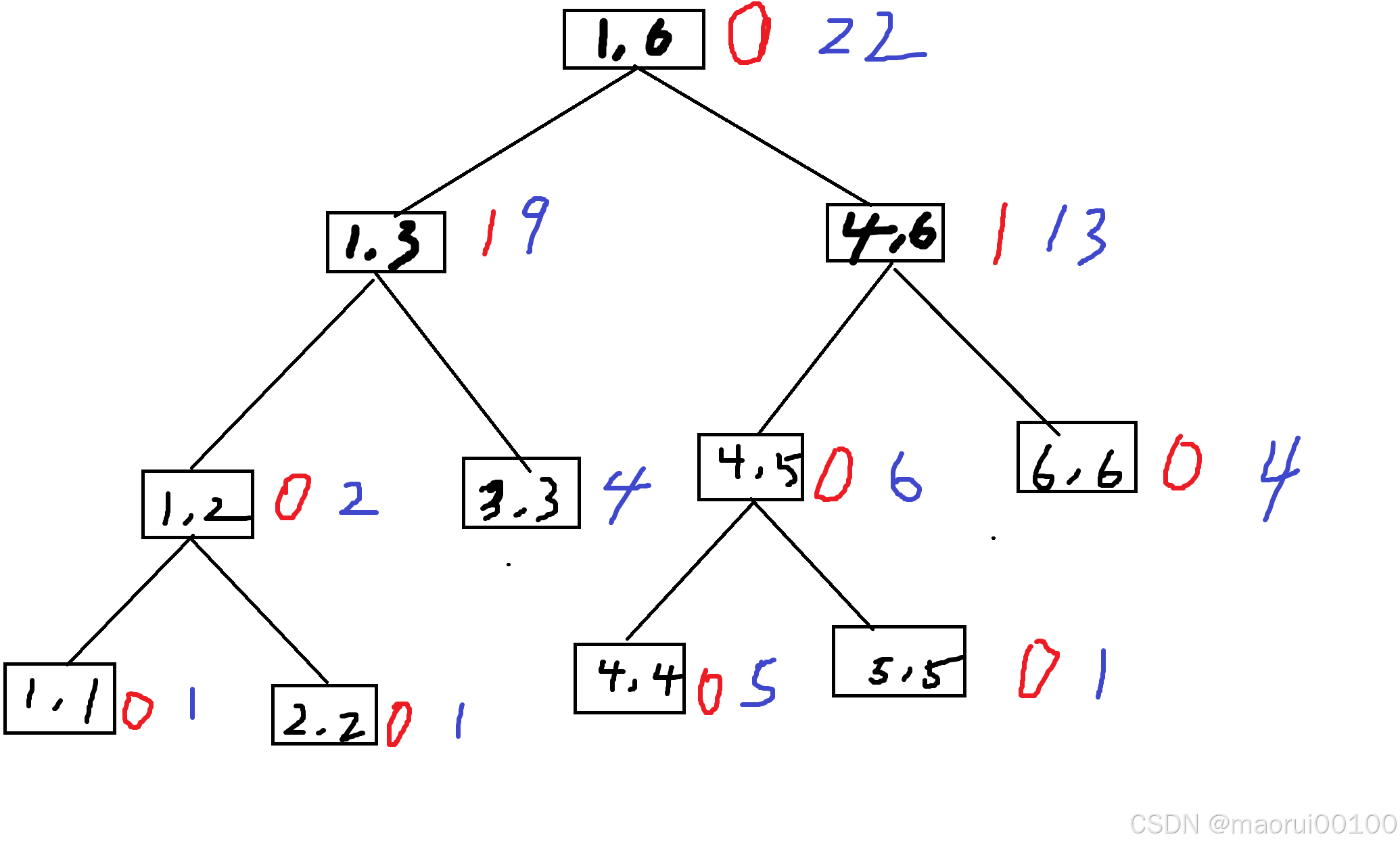
这时我们向下递归，先是查到（1,3），这时我们发现已经被包含了

于是向上一步那样，我们开始修改

 

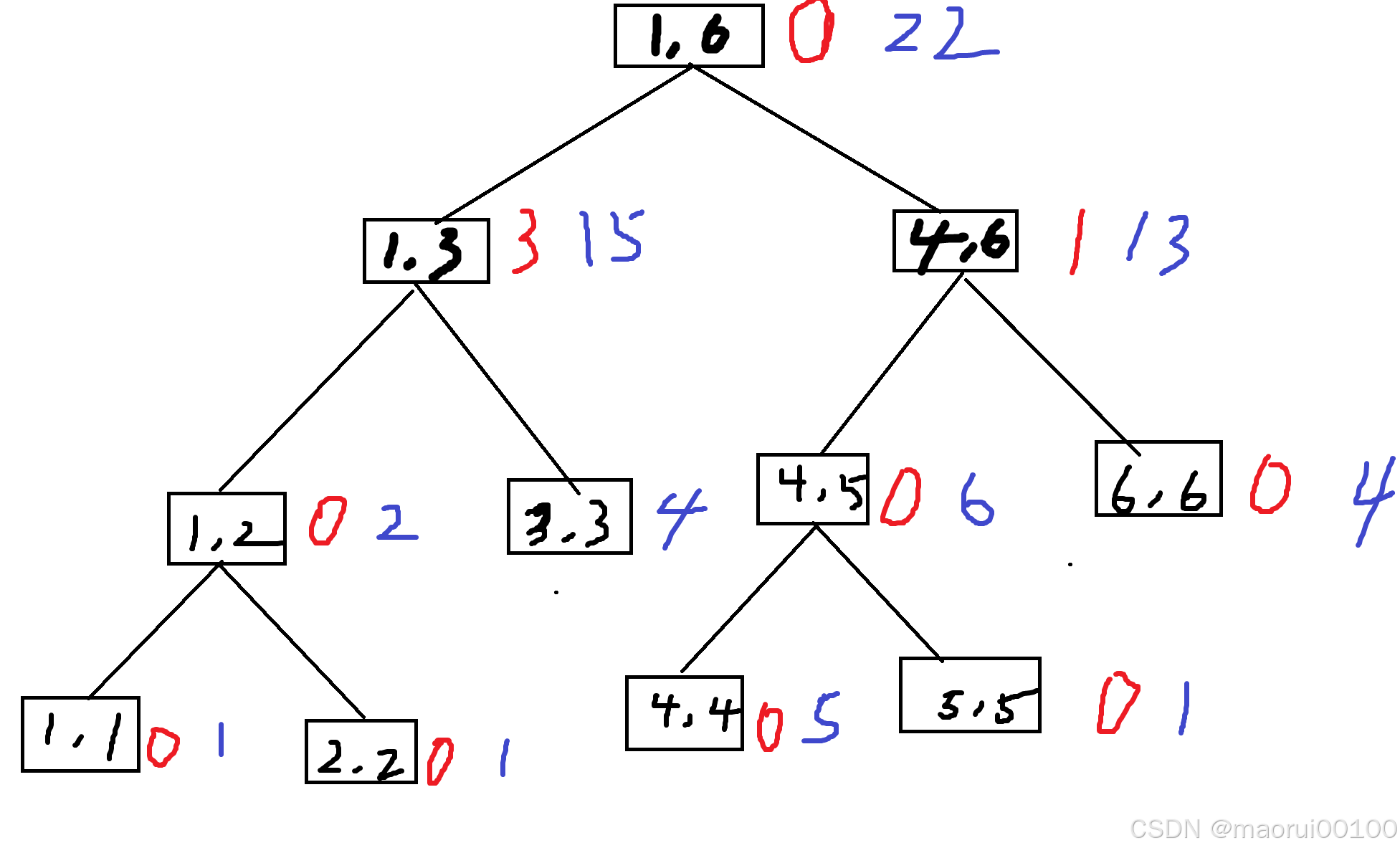
到了这里相信大家已经明白了

我们需要进行的无非就是不断的下放，知道遇到恰好被包含的区间即可

接下来给出代码

void push_down(int id,int l,int r)//下放操作
{
	if(lazy[id])
	{
		int mid=(l+r)/2;
		lazy[id*2]+=lazy[id];
		lazy[id*2+1]+=lazy[id];
		sum[id*2]+=lazy[id]*(mid-l+1);
		sum[id*2+1]+=lazy[id]*(r-mid);
		lazy[id]=0;
	}
}
void qjgx(int l,int r,int x,int y,int k,int id)
{
	if(l>=x&&r<=y)//遇到被包含区间
	{
		lazy[id]+=k;
		sum[id]+=k*(r-l+1);
		return;
	}
	push_down(id,l,r);
	int mid=(l+r)/2;
	if(x<=mid)
	{
		qjgx(l,mid,x,y,k,id*2);
	}
	if(y>mid)
	{
		qjgx(mid+1,r,x,y,k,id*2+1);
	}
	sum[id]=sum[id*2]+sum[id*2+1];//注意在回溯时重新记录一下
}

 最后一步便是区间查找了

还是一样，如果恰好查到最好，查不到我就下放呗

int find(int l,int r,int x,int y,int id)
{
	if(l>=x&&r<=y)
	{
		return sum[id];
	}
	push_down(id,l,r);
	int mid=(l+r)/2;
	int ans=0;
	if(x<=mid)
	{
		ans+=find(l,mid,x,y,id*2);
	}
	if(y>mid)
	{
		ans+=find(mid+1,r,x,y,id*2+1);
	}
	return ans;
}

这就是线段树的几种基本模版

希望能帮到大家