定义
B-tree 即 B树,B 即 Balanced,平衡的意思。
B树 是一颗多路平衡查找树。
B 树又叫平衡多路查找树。一棵m阶的B 树 (m叉树)的特性如下:
1.根节点至少有两个孩子 。
2.每个非根节点至少有M/2(上取整)个孩子,至多有M个孩子。
3.每个叶子节点 至少有 M/2-1(上取整)个关键字,至多有 M-1 个关键字。并以升序排列。(注:叶子节点是没有孩子)
4.key[i] 和 key[i+1] 之间的孩子节点的值介于 key[i] 和 key[i+1] 之间。
5.所有的叶子节点都在同一层。
拓展
1.B树的 阶数 是指 树中 的 最多子节点个数。比如,2-3树的阶是3,2-3-4树的阶是4;
2.B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
3.关键字集合分布在整棵树中, 即叶子节点和非叶子节点都存放数据;
4.搜索有可能在非叶子结点结束;
5.其搜索性能等价于在关键字全集内做一次二分查找;
B树的插入操作
插入操作是指插入一条记录,即(key, value)的键值对。如果B树中已存在需要插入的键值对,则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。
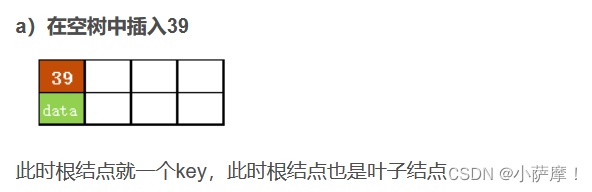
1)根据要插入的key的值,找到叶子结点并插入。
2)判断当前结点key的个数是否小于等于m-1,若满足则结束,否则进行第3步。
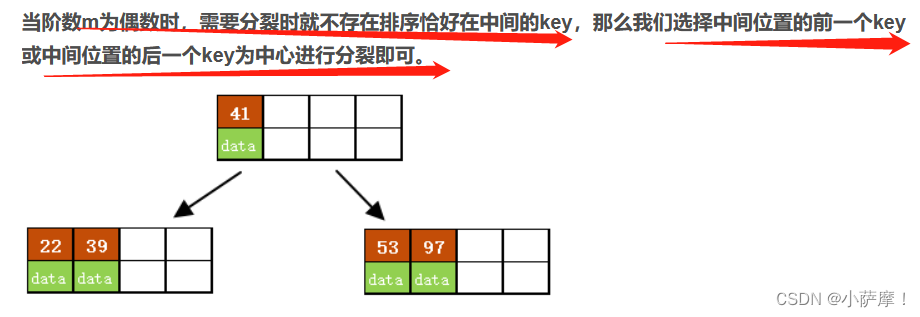
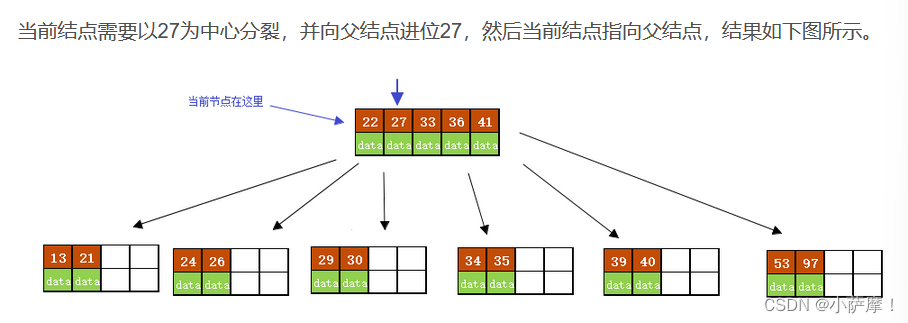
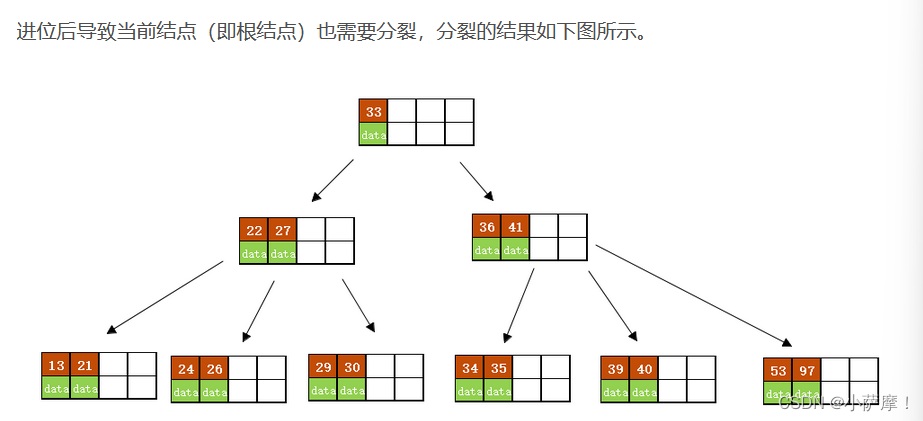
3)以结点中间的key为中心分裂成左右两部分,然后将这个中间的key插入到父结点中,这个key的左子树指向分裂后的左半部分,这个key的右子支指向分裂后的右半部分,然后将当前结点指向父结点,继续进行第3步。( 当阶数m为偶数时,需要分裂时就不存在排序恰好在中间的key,那么我们选择中间位置的前一个key或中间位置的后一个key为中心进行分裂即可。 )


插入后超过了最大允许的关键字个数4,所以以key值为41为中心进行分裂,结果如下图所示,分裂后当前结点指针指向父结点,满足B树条件,插入操作结束。
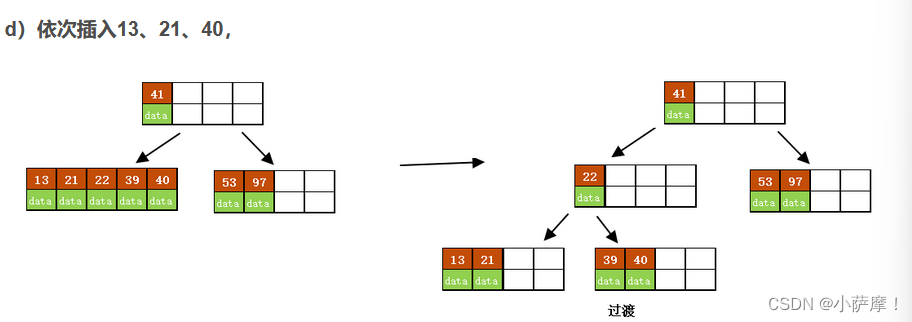
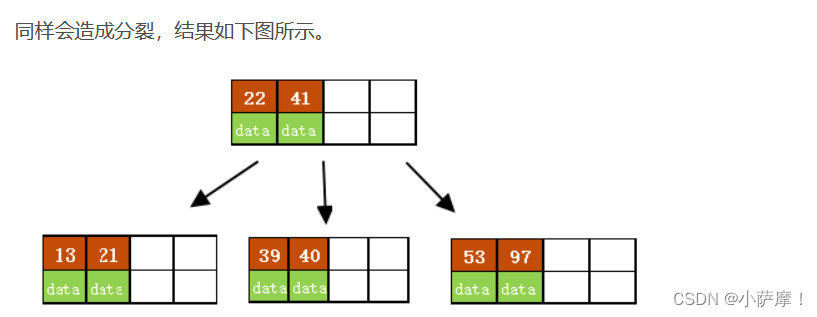
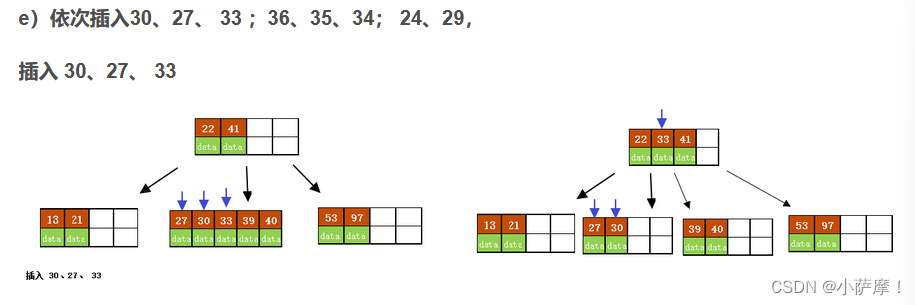
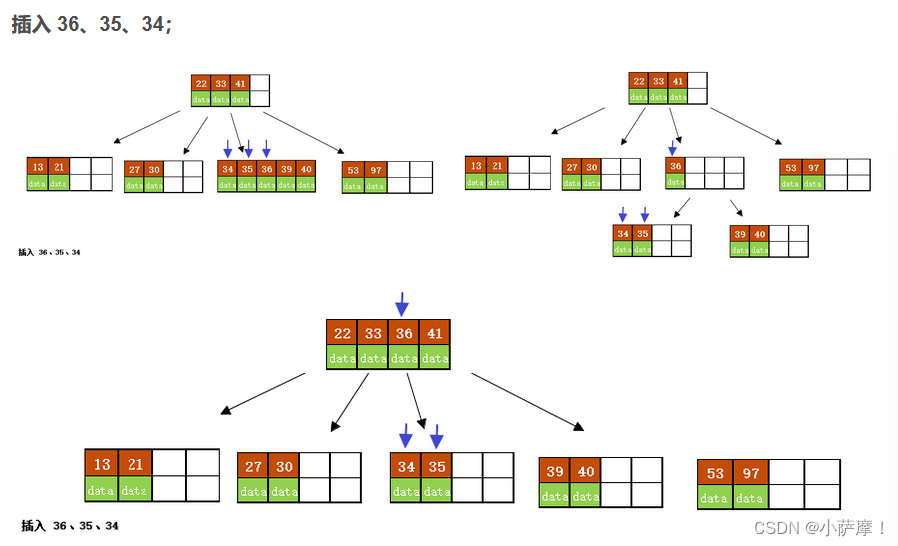
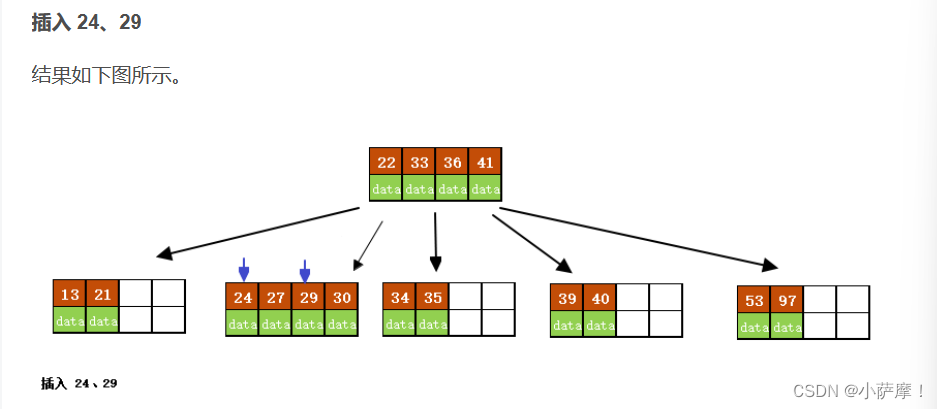
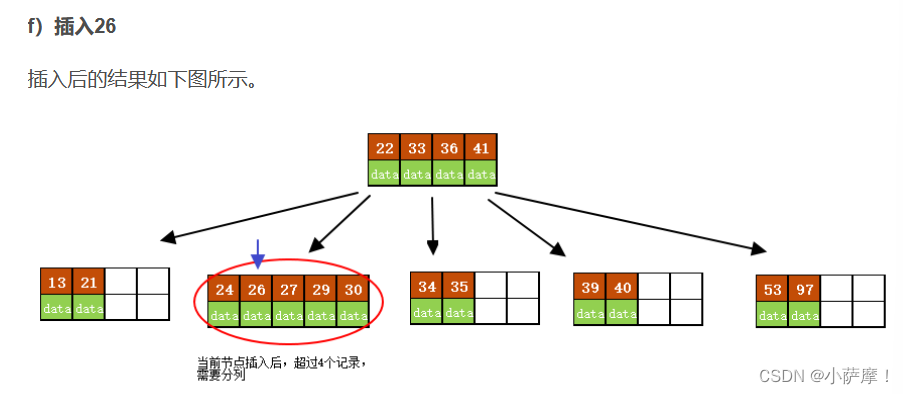
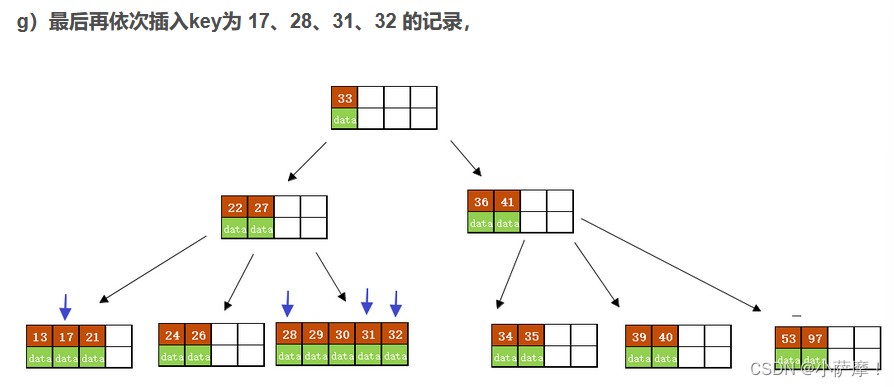
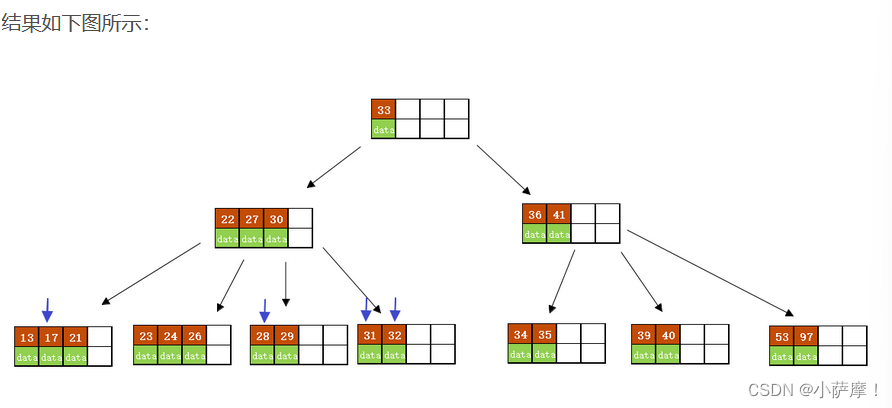





 B树是一种平衡多路查找树,保证了数据查找的效率。在插入操作中,如果叶子节点的关键字数量未超过最大限制,则直接插入,否则需分裂节点并将中间键上移。B树的搜索性能类似于二分查找。
B树是一种平衡多路查找树,保证了数据查找的效率。在插入操作中,如果叶子节点的关键字数量未超过最大限制,则直接插入,否则需分裂节点并将中间键上移。B树的搜索性能类似于二分查找。
















 1426
1426

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








