了解Transform基本原理

BERT是基于transformer的，在理解BERT之前，需要先了解transformer。Transformer就是将模型中lstm或者RNN结构替换成attention结构，这里就涉及了attention结构。

1. attention

• Attention由来的背景：

RNN模型在解决序列问题上具有一定优势，下图中的左半部分展示了一个双向RNN结构，但通过RNN输出的序列数据不容平行化，例如，b4是融合了a1,a2,a3,a4的基础上才能够得出来，在得出b4之前，需要先计算出b1、b2、b3，这是一个迭代的过程。当然可以考虑使用CNN来实现序列数据平行化，但CNN是通过卷积核的不断划动进行卷积操作，每次卷积只涉及句子的部分信息，不能考虑全局信息。而attention机制则是解决了两者的缺点，及考虑了句子的全局信息，同时实现平行化过程。下图的右半部分展示了Self-attention，可以简单直观理解，self-attention是一个黑盒子，经过它即能输出序列数据，同时也考虑了序列数据的全局信息，且可以平行化。

2. self-attention

• self-attention layer层内部原理

self-attention layer层内部到底是如何运作，上左图所示，x1、x2、x3、x4为序列数据的输入，将它们与**权重向量**乘积后得到了a1,a2,a3,a4、a1,a2,a3,a4分别与**不同权重**向量相乘后，会产生q、k、v，其中，q为query是用来匹配的，K为key是用来被匹配的，v是每个token被提取到的信息，利用每个q分别对每个k进行attention（attention的过程其实直观理解就是将两个向量运算后得到一个分值，当然可以使用不同的方法进attention），attention后的值经softmax后将与每个v相乘求和即为b1的输出。下图简单表示运算过程：

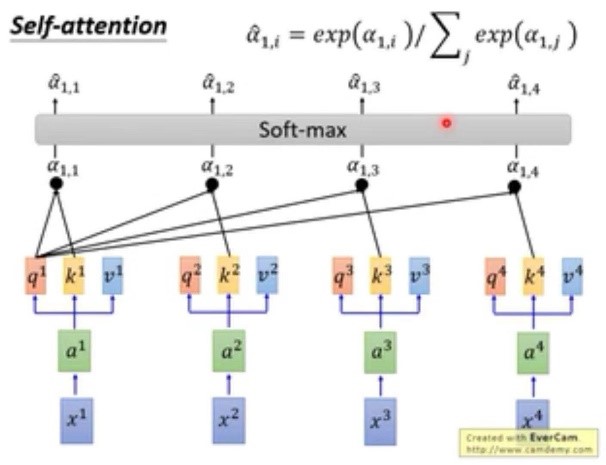
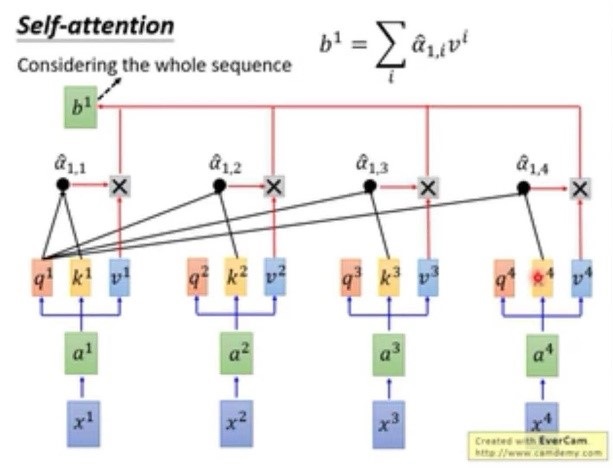
• Attention的平行化

下图表示Attention的平行化，在计算b1的同时是可以计算b2的，两者可以同时进行，没有影响，且b2的输出也包含句子的全部信息。

矩阵表达如下：

展示了经过self-attention后的输入I与输出O：

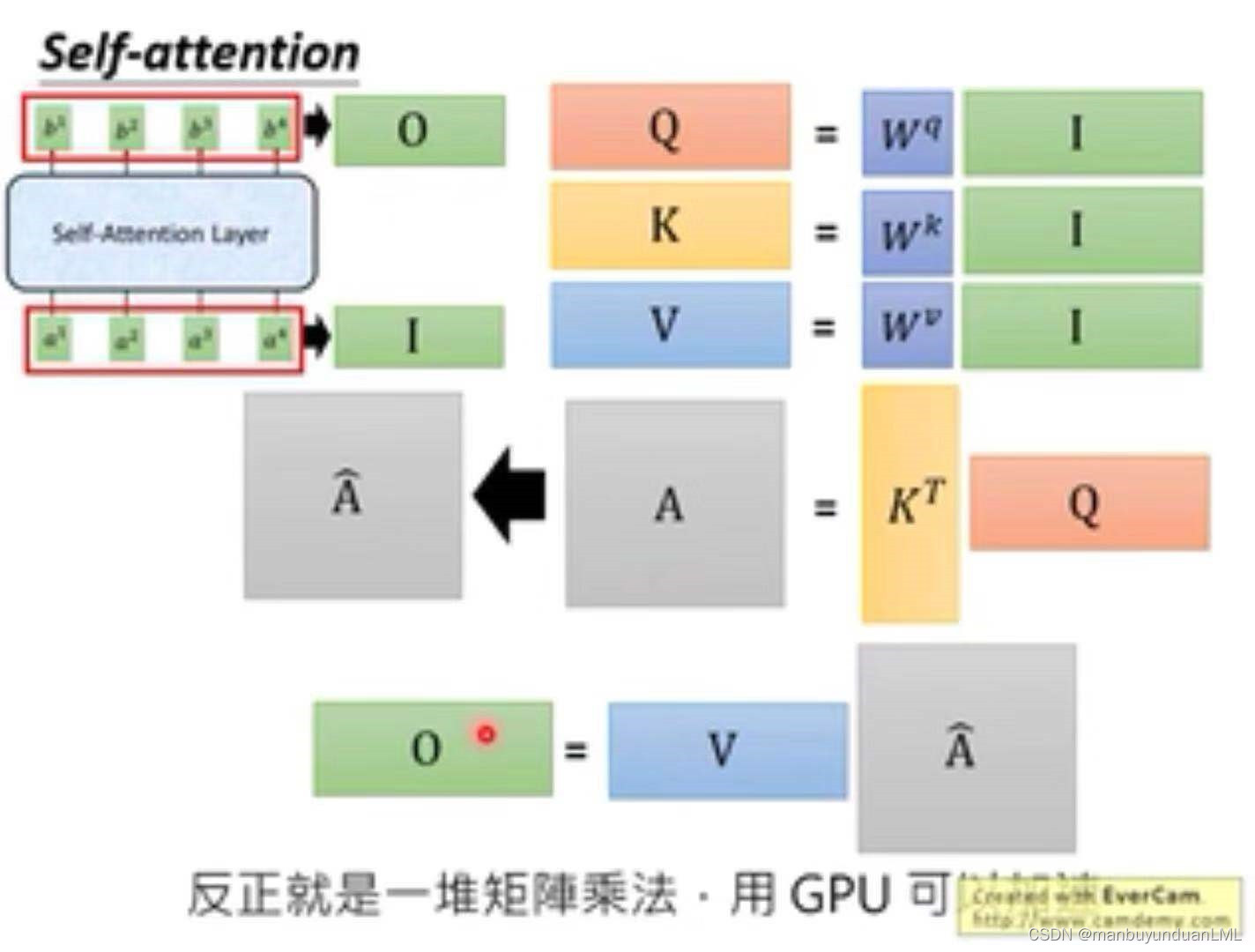综上所述，self-attention是一堆矩阵的乘法运算，GPU可实现其加速过程。

3. multi-head self-attention

下图展示了2个head的self-attention，其中q只能与同样位置的K进行点乘，之所以会选用这种方式是因为每个head的关注点不一样，有的关注句子的局部信息local haed,有的则关注全局信息globel head。对于输出的bi,1与bi,2最终可通过连接和降维等方式输出最后的bi。

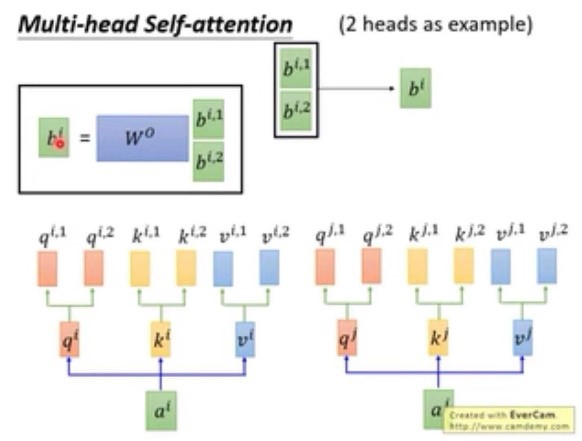
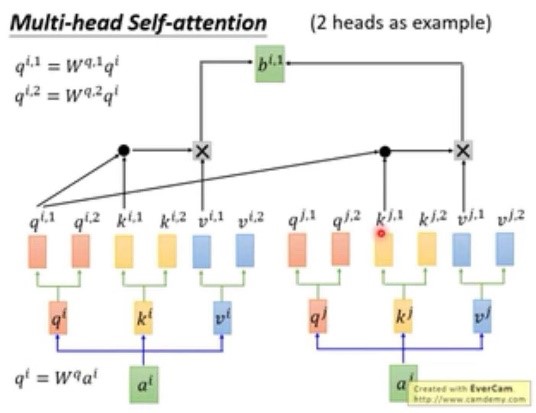
• 位置信息
  Self-attention是没有考虑位置信息，在原始论文中涉及了位置信息：在ai处增加了相同维度的位置向量ei,该向量不是从数据中得来，是人工设定的，反映不同的位置信息。当然，也可采用其他方式来体现位置在这里的作用。