SRM 565 div1

250pts

直接dp，f[i][j]表示到i花费为j怪的最大价值和。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
int n;
ll f[51][110],ans;
void upd(ll &x,ll y){x=max(x,y);}
class MonstersValley
{
public:
    int minimumPrice(vector<ll>v1,vector<int>v2)
    {
        n=v1.size();
        memset(f,-1,sizeof(f));
        f[0][0]=0;
        for(int i=1;i<=n;i++)
            for(int j=0;j<=(i-1)*2;j++)
                if(f[i-1][j]!=-1)
                {
                    upd(f[i][j+v2[i-1]],f[i-1][j]+v1[i-1]);
                    if(f[i-1][j]>=v1[i-1])
                        upd(f[i][j],f[i-1][j]);
                }
        for(int i=n*2;i>=0;i--)
            if(f[n][i]!=-1)ans=i;
        return ans;
    } 
}cls;

500pts

这是一个nim问题。可以将每个数看成质因子个数个石子。一段区间满足条件当且仅当这段区间的石子个数异或值为0。
因此需要求每个数质因子的个数。
筛出$\sqrt{n}$以内的素数，然后枚举所有素数，把[L,R]中所有这个数的倍数中的这个质因子提出来。
如果最后剩的不为1，那么质因子个数+1。
然后处理一个异或前缀和，任意两个相等的前缀和可以组成一段区间。

#include <bits/stdc++.h>
using namespace std;
#define N 1100000
#define ll long long
int prime[N],ip[N],cnt;
int val[N],sum[N],a[N];
ll ans;
void init()
{
    for(int i=2;i<=100000;i++)
    {   
        if(!ip[i])prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<=100000;j++)
        {
            ip[i*prime[j]]=1;
            if(i%prime[j]==0)break;
        }
    }
}
class TheDivisionGame
{
public:
    ll countWinningIntervals(int L,int R)
    {
        init();
        for(int i=L-1;i<=R;i++)a[i-L+1]=i;
        for(int i=1;i<=cnt;i++)
            for(int j=R/prime[i]*prime[i];j>=L-1;j-=prime[i])
            {
                while(a[j-L+1]%prime[i]==0)
                    a[j-L+1]/=prime[i],val[j-L+1]++;
            }
        for(int i=0;i<=R-L+1;i++)
            if(a[i]!=1)val[i]++;
        for(int i=0;i<=R-L+1;i++)
            val[i]^=val[i-1],sum[val[i]]++;
        for(int i=0;i<=200;i++)
            ans+=(ll)sum[i]*(sum[i]-1)/2;
        return (ll)(R-L+2)*(R-L+1)/2-ans;
    }
}cls;

1000pts

一个巨大的分类讨论。（我应该写麻烦了）。
分A,B,C呈Y字形和A,B,C在一条链上讨论。

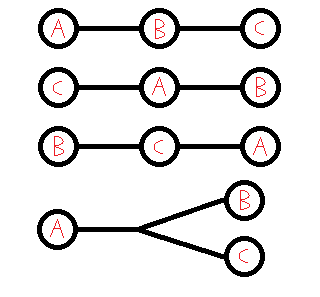
如果Y字形枚举中间点。然后看其他点在Y字的哪个部分。一个点只有可能在一个部分中。

然后枚举情况解方程。
对于一条链的情况更麻烦一些。
注意判重。

#include <bits/stdc++.h>
using namespace std;
#define mod 1000000009
#define ll long long
int n,ans,now;
int d[61][3],st[61][61],top[61];
int val[61],cnt,f[61],pos[3],bel[3];
int X,Y;
struct node
{
    int x,y;
    node(){}
    node(int x,int y):x(x),y(y){}
}dis[3][61],dis1[61];
int num[3],num1;
int get(int a,int b,int d1,int d2)
{
    if((d1+d2-a-b)&1)return 0;
    Y=(d1+d2-a-b)/2;
    X=(d2-d1-b+a)/2;
    if(X<0||Y<0)return 0;
    return 1;
}
void cal(int &sum)
{
    for(int i=1;i<=cnt;i++)
        if(top[i])
        {
            sort(st[i]+1,st[i]+1+top[i]);
            if(st[i][1]!=0){sum=0;return;}
            f[1]=1;
            for(int j=2;j<=top[i];j++)
            {
                f[j]=0;
                for(int k=1;k<j;k++)
                    if(st[i][j]!=st[i][k])
                        f[j]=(f[j]+f[j-1])%mod;
            }
            sum=(ll)sum*f[top[i]]%mod;
        }
}
int solve1(int x)
{
    cnt=0;int sum=1;
    memset(num,0,sizeof(num));
    for(int i=0;i<3;i++)
    {
        val[++cnt]=d[x][i];
        dis[i][++num[i]]=node(d[x][i],0);
    }
    for(int i=0;i<n;i++)
    {
        int flag=-1;
        for(int j=0;j<3;j++)
            if(get(d[x][j],d[x][(j+1)%3],d[i][j],d[i][(j+1)%3]))
            {
                if(d[x][(j+2)%3]+X+Y!=d[i][(j+2)%3])continue;
                flag=j;val[++cnt]=X;
                dis[j][++num[j]]=node(X,Y);
                break;
            }
        if(flag==-1)return 0;
    }
    sort(val+1,val+1+cnt);
    cnt=unique(val+1,val+1+cnt)-val-1;
    for(int i=0;i<3;i++)
    {
        memset(top,0,sizeof(top));
        for(int j=1;j<=num[i];j++)
        {
            dis[i][j].x=lower_bound(val+1,val+1+cnt,dis[i][j].x)-val;
            st[dis[i][j].x][++top[dis[i][j].x]]=dis[i][j].y;
        }
        cal(sum);
    }
    return sum;
}
void upd(int x,int y)
{dis1[++num1]=node(val[++cnt]=x,y);}
int solve2(int x,int a,int b,int c,int tp)
{
    if(a>c)return 0;
    memset(top,0,sizeof(top));
    cnt=0;int sum=1,d1,d2,dx,dy;
    num1=0;
    if(tp==0)
    {
        upd(0,0);upd(dx=d[x][a],dy=0);
        upd(d1=d[x][a]+d[x][b],0);
        upd(d2=d[x][a]+d[x][c],0);
    }
    else if(tp==1)
    {
        upd(0,0);upd(dx=d[x][a],dy=0);
        upd(d1=d[x][a]-d[x][b],0);
        upd(d2=d[x][a]+d[x][c],0);
    }
    else if(tp==2)
    {
        upd(0,0);upd(dx=0,dy=d[x][a]);
        upd(d1=d[x][b]-d[x][a],0);
        upd(d2=d[x][c]-d[x][a],0);
    }
    else if(tp==3)
    {
        upd(0,0);
        upd(d1=d[x][a]-d[x][b],0);
        upd(d2=d[x][c]-d[x][b]+d1,0);
        upd(dx=d1,dy=d[x][b]);
    }
    else
    {
        upd(0,0);
        upd(d2=d[x][a]-d[x][c],0);
        upd(d1=d2-(d[x][b]-d[x][c]),0);
        upd(dx=d2,dy=d[x][c]);
    }
    if(d1<0||d2<0||d1>=d2)return 0;
    for(int i=0;i<n;i++)
        if(i!=x)
        {
            if((d[i][a]+d[i][c]-d2)&1)return 0;
            X=(d[i][a]-d[i][c]+d2)/2,Y=(d[i][a]+d[i][c]-d2)/2;
            if(X<dx||(X==dx&&Y<dy)||(X==dx&&Y==dy&&i<x)||Y<0||X>d2)return 0;
            if(X<=d1&&d1-X+Y==d[i][b])
            {
                val[++cnt]=X;
                dis1[++num1]=node(X,Y);
                continue;
            }
            if(X>d1&&X-d1+Y==d[i][b])
            {
                val[++cnt]=X;
                dis1[++num1]=node(X,Y);
                continue;
            }
            return 0;
        }
    sort(val+1,val+1+cnt);
    cnt=unique(val+1,val+1+cnt)-val-1;
    for(int i=1;i<=num1;i++)
    {
        dis1[i].x=lower_bound(val+1,val+1+cnt,dis1[i].x)-val;
        st[dis1[i].x][++top[dis1[i].x]]=dis1[i].y;
    }
    cal(sum);
    return sum;
}
class UnknownTree
{
public:
    int getCount(vector<int>da,vector<int>db,vector<int>dc)
    {
        n=da.size();
        for(int i=0;i<n;i++)
            d[i][0]=da[i],d[i][1]=db[i],d[i][2]=dc[i];
        for(int i=0;i<n;i++)
            ans=(ans+solve1(i))%mod;
        for(int i=0;i<n;i++)
            for(int j=0;j<3;j++)
                for(int k=0;k<5;k++)
                {
                    ans=(ans+solve2(i,j,(j+1)%3,(j+2)%3,k))%mod;
                    ans=(ans+solve2(i,j,(j+2)%3,(j+1)%3,k))%mod;
                }
        return ans;
    }
}cls;