早点关注我，精彩不错过！
MatheMagcian数学魔术师种子班2025（下）火热报名中！
首次增加面向1-3年级孩子和教师的内容，所有主题全部更新！
欢迎点击《用魔术把数学放进孩子心里！——2025（下）数学魔术师种子班报名通知（内含惊喜福利）》和咨询微信1035312177（备注：数学魔术课程咨询）报名！
名额有限，先到先得！
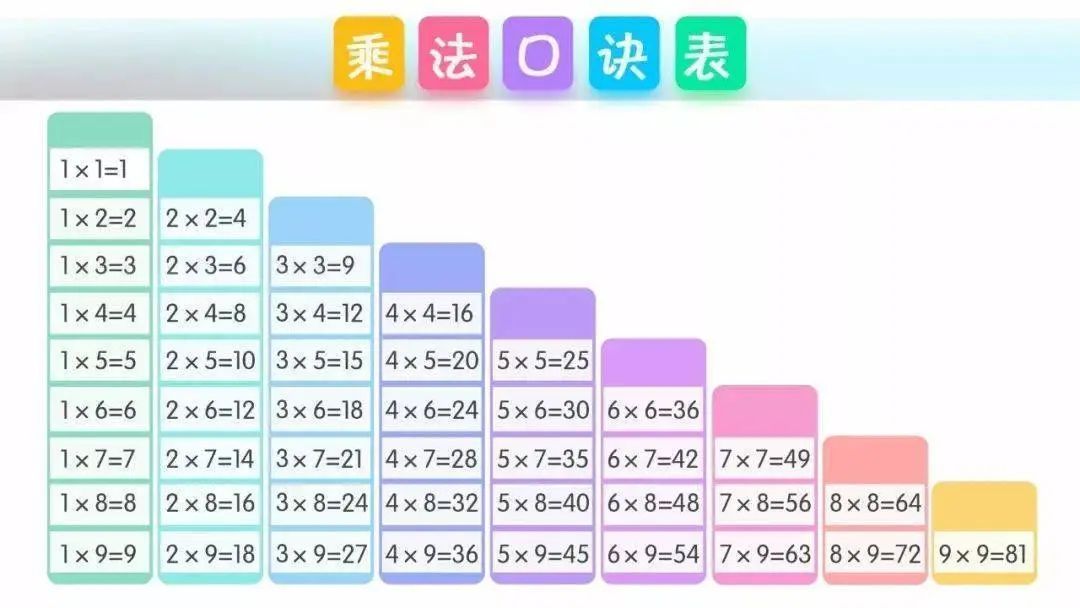依稀记得我还没进小学的时候，我的父亲按着我在奶奶家一楼门口的开放阳台上死记硬背乘法口诀表的那个下午。我一边哭着一边背，一边远望斜坡对面的篮球场，好想不背了去打场球。
然而后来进了学前班，发现我凭借这一张表在班上的数学课上乱杀特杀，甚至还有前后女同学投来的欣赏的目光，又依稀给了我一点点安慰。
再到后来数学老师经常给我们在课上甩10道百位数的乘法作竖式练习，我总是能第一个完成，又积累了一些虚无的自信。
……
暂停。
每个人的经历不可复制，各有深刻的记忆点和个人值得反思的时刻，这些除了当故事听外，对新学习孩子的价值都有限。也别指望着作为家长/老师，倚老卖老地觉得自己小学数学小菜一碟，就可以替代孩子做决定，并按照自己已经是过来人的独特的经验去灌输。个人体验和教学经验顶多作为一点参考养料。至于孩子吃不吃，愿意怎么吃，还得具体来看。
本文提出我对小学算术的理解，回忆我个人曾经背乘法口诀表的一些思考碎片，并由此提出死记硬背如何和理解为先进行交叉结合的学习方法，希望能以小见大。
小学算术的降维认知
小学算术（课程标准的说法是数与运算加上数量关系，构成数与代数的教学目标），本质上是一套用十进制数编码的整数和分数的四则运算的数学模型和算法问题。数学模型藏在不厌其烦地把自然数和生活和考试中各种苹果梨子排队的对应过程中，关于“什么场景可以数数”的训练其实很像训练AI“什么图像是一只猫”的过程一样，也是非严谨逻辑和经验式的。自然数分为基数和序数两种应用模型，分别描述集合的大小和在链条上的位次和其上的加法；接着为表达反方向/欠的含义引入负数和减法；然后是加法简便运算的乘法引入以快速计算，及其分蛋糕问题中用分数和小数解决1以下量的表达。如果认真去想，每一道小学算术题都可以看到它考察的是哪类数学模型。
而算法问题指的是，在运用四则运算这一套数学工具时，小学生们并没有被要求严谨地理解背后的完整数学结构，而只是安全地在使用它，而且是使用它在十进制编码数字下的副本。即，只要记忆并正确执行这些指令和其复合就行。结构的话，不要求掌握，超出了全民义务教育小学生的水平要求了。
但还是想从抽象代数的观点补充一下这个数学结构的实质。从和数数过程对应的自然数开始（自然数加法幺交换半群，封闭、结合、幺元、交换），接着引入负数（添加逆元的整数加法（交换）群），再添加其上的简便运算乘法（添加乘法幺（交换）半群，满足分配率，无零因子的整（数）环，即无零因子的交换环），接着再添加乘法的逆运算除法（添加乘法非加法幺元（零元素）的逆元构成除环，即可交换除环）。这就是小学算术的全部数学结构了，一般孩子不用理会，但教的人自己心里有谱应该有点用。
乘法口诀表为什么要背？
回到小学算术的算法问题。按教材的教法，这里所有的计算都是从整数加法开始的。通过理解和记忆的融合先是搞定了结果或加数在10以内的加法的编码表，接着是其逆运算减法的倒查表。加上各种凑/借十法转化为和10相关的加减法编码表，来计算20以内结果的加减法（两个加数都是个位数，被减数在20以内）。接着是超出范围的竖式计算：有一个加数超过10则在不同位分别计算后进位+1，或者被减数超过20也只借1位，转化为一个- 1和仍然10几为被减数的减法（当本来是0的时候例外为9）。
然后是加法的简便运算乘法。先记下来个位数乘法的编码表，配合加法用竖式解决多位数的乘法问题。再逆运算为除法和分数，也分为带余除法和小数近似的算法。小数是十进制下的特殊分数，而所谓等分除和包含除则是更细致的除法含义的模型了。而好像没有人去倒着背乘法口诀表，而且即使背了也容易因为除不尽而查无此数，因此有了根据快速的大小比较形成“试商”的竖式除法算法。
值得一提的是，竖式运算我们都很熟悉，其本质是每一个子操作的计算内容又化归到之前至少有1个是个位数的用口诀就能解决的问题上。稍微难一点的是除法，需要试商以及表里没有的1位和多位数的结果还需要进一步估算才能完成试商，不断估计来得到结果。但孩子可能从来没关注过其正确性的证明和理解，其背后有各种近似计算，进制数的含义、分配率、结合率才保证这套算法成立的，可以说是一套十进制下的人脑计算算法。如果只记得执行步骤，不了解算法正确的原因，那实在是非常可惜。
你看到了吧，这所有算法的一切，都基于最原始的两张表：10以内的加法表（1 + 2 + …… + 10 = 55条）和个位数乘法表（9 * 9 = 81条）。有点类似于二进制计算机用逻辑运算表达出来的仅有的4条加法规则，而我们偏要用10进制才导致底层要记忆的口诀复杂度如此之高。而后续的各种破十/借十的扩展，简直就是在为这复杂的算法达补丁，不然记忆负担就要继续加大了！我自然地把它理解为惯性力量下后代为前人堆积的不良习惯还账，都怪那个一开始认为手指脚趾的数量就是最好的进制值的人。
没错，这就是乘法口诀表为什么要背！我是需要掌握计算算法来应对生活和考试的要求，但可能不至于要用这么复杂的编码规则和计算方法。而你没听错，我们不假思索没得选择地去背它，就因为人类的历史习惯在还账！
但也别这么说，这也算是人类留下的，沿袭上帝旨意的优秀文化。
你可别小看了这个文化带来的不兼容性，不信你换个7进制的数，再做一把3位数乘法看看，能一次性不出错的都是天才。
于是只好放弃了造反，接纳了，再也不说能不能不背十进制的表，改成在脑海里用二进制4条规则计算的这种不在可行空间的事了。且不说后续竖式扩展部分的计算次数更多，也没有发挥人脑记忆这百来条规则的高速缓存的能力，效率不见得就更高。但就考试时候可能要写中间过程，以及多了适应其他人类编解码的工作，就够喝两壶的了。相当于你的脑子一直和别人运行的都不是一套语言，一旦出问题或者要深入细节和经验，就难以沟通了。
那能不能像查元素周期表一样查表，不用背呢？理论上当然可以，前提是不考虑完成计算的效率，每一步也不会出错的情况下。即不需要考虑时间维度的变量，那自然印一张表就好了，何必背呢？但问题是，无论是考试还是真实的生活运算场景，速度因素都是积少成多非常重要的，在有限的条件下，规定时间内没有快速地完成，就等于不会，竞争不过，错过时机。另外，人类每一步操作的错误率明显做不到机器，查表不仅效率低，而且在不熟悉答案的情况下，错误率也高，也没有所谓数感来完成更多的校验以降低它。
当然这一点也要辩证地来看，比如从算盘到计算器再到AI，借助工具的效果和效率都可能逐步显著高于记忆的效果，更别提要花费的记忆成本了。生活中确实逐步可以用计算器替代就是例子。但是学校教育往往是滞后于社会发展的，这方面显然我们的跨步也大大地不如西方对于计算器那么地开放。因此在考试的竞争场景，快速地背诵还是有其功利价值。另外，背诵完成带来的赋予自身的能力的自信感，以及过程中习得的学习习惯、方法和顺道对内容的结构理解，也非常有收获，不见得省了这点背诵的时间就去跳上去理解效率就真的更高。这都是看似没有走用工具的路的旁的收获，既然不容改变，那就利用好吧！
因此，无论是基于不可改变的人类算术环境的适应，还是基于效率和准确率的考虑，为了达成算术能力养成的目标，乘法口诀表都非背不可！而且是那种要求滚瓜烂熟，速度超快，准确率超高的记忆级别。
下篇文章我们继续聊聊，既然乘法口诀表避不开要背，那要怎么背吧！
下期见！
我们是谁：
MatheMagician，中文“数学魔术师”，原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义，也取像魔术一样玩数学的意思。文章内容涵盖互联网，计算机，统计，算法，NLP等前沿的数学及应用领域；也包括魔术思想，流程鉴赏等魔术内容；以及结合二者的数学魔术分享，还有一些思辨性的谈天说地的随笔。希望你能和我一起，既能感性思考又保持理性思维，享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流！
扫描二维码
关注更多精彩
明明有bug的扑克魔术怎么还能骗到人？（五） ——大效果前，小瑕疵后
2024阿里巴巴全球数学竞赛决赛中的深度学习背景题解析（二）——应用与计算数学部分第6题
完美洗牌的秘密（二十一）——milk shuffle的应用三（天天四条龙等）
点击阅读原文，往期精彩不错过！
扫一扫
3617
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
