电磁学、磁电学与磁电子学

孙阳

重庆大学教授

电磁学与磁电学是一回事吗？不是的。

磁电学与磁电子学是一回事吗？也不是。

电磁学electromagnetism

电磁学是研究宏观电磁现象以及电与磁交互关联的物理学分支学科。众所周知，电磁学的精髓可以用麦克斯韦方程组来概括：

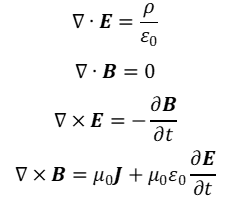
其中的电场和磁场是根据电荷受力（库仑力和洛伦兹力）来定义的场。第一个方程描述了静电场的特征——静电场是有源场，来源于电荷；第二个方程描述了静磁场的特征——静磁场是无源场，散度为零；第三个和第四个方程描述了电场和磁场的关联——变化的磁场可以产生电场，电流或变化的电场可以产生磁场。

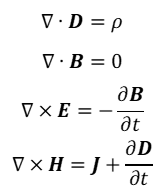
以上是真空中的麦克斯韦方程组，当存在非真空的介质时，麦克斯韦方程组需要改写。为了描述介质中的电磁现象，人们定义了一些物理量：电极化强度，电位移矢量，磁化强度，磁感应强度。由此，可以得到介质中的麦克斯韦方程组：

上述介质中的麦克斯韦方程组其实隐含了一个前提假设，即：对于常规的介质，外加磁场会在介质内部诱导出磁化强度，外加电场会在（绝缘）介质内部诱导出电极化强度，如图1所示。

图1 常规介质对外加磁场和电场的响应

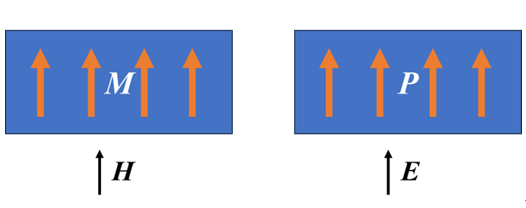
那么，有没有这样一类介质？外加磁场不仅产生磁化强度而且可以诱导出电极化强度，外加电场不仅产生电极化强度而且可以诱导出磁化强度，如图2所示。

图2 磁电耦合效应示意图

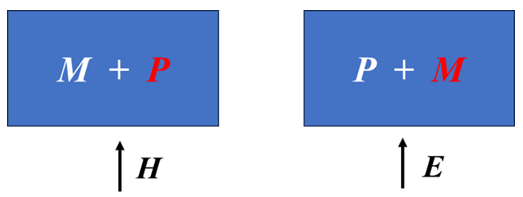
这种由磁场诱导电极化强度和电场诱导磁化强度的现象被称为磁电效应（magnetoelectric effects）。为了强调这是磁和电之间的一种非常规耦合现象，人们也常常把magnetoelectric effects翻译为磁电耦合效应。

显然，对于存在磁电耦合效应的介质，经典麦克斯韦方程组将不足以描述其中的电和磁交互关联的行为。

这样的磁电耦合介质是否真的存在呢？答案是肯定的。

近二十年来，对介质中磁电耦合效应的研究正逐渐发展成为一门新兴的前沿分支学科——磁电学。

磁电学magnetoelectricity

关于磁电耦合效应的研究最早可以追溯到19世纪末。1894年，法国物理学家居里先生（Curie）基于晶体的对称性理论，预言了某些晶体中可能会存在一种本征的磁电耦合效应[1]。1926年，荷兰物理学家德拜（Debye）在总结了前人一系列不太成功的实验后，提出了“magneto-electrical effect”这一名词[2]。

1950-1960年代，前苏联科学家在磁电耦合效应的理论和实验研究方面做出了突破性的贡献。朗道（Landau）和栗弗席兹（Lifshitz）在1960年出版的《连续介质的电动力学》（Electrodynamics of Continuous Media）一书中，已经有关于磁电耦合效应的详细理论描述。1959年，Dzyaloshinskii理论预言了反铁磁体Cr₂O₃中存在磁电耦合效应[3]，随后于1960年被Astrov在实验中证实[4]。Cr₂O₃成为第一个被确认的磁电耦合材料。

在此后的十多年里，人们又陆续发现了几十种具有磁电耦合效应的材料。然而，这些材料中的本征磁电耦合效应都很微弱，并无任何应用价值。因此，这些关于磁电耦合效应的早期研究并没有引起太多的关注。

1970年代以后，人们想到了一种增强磁电耦合效应的策略：让铁磁性和铁电性在一种材料中共存，从而有可能促进磁性和电性之间的相互耦合。这一策略直接产生了复合磁电材料（即把铁电体和铁磁体复合在一起，通过两相的界面产生间接的磁电耦合），并催生出了多铁性（multiferroicity）、多铁性材料（multiferroic materials）、多铁体（multiferroics）和磁电体（magnetoelectrics）等新概念和新名词[5]。

2003年，日本东京大学Tokura研究组在TbMnO₃中实现了磁场调控电极化，第一次演示了单相材料中较大的本征磁电耦合效应[6]。这一重大发现重新唤醒了人们对磁电耦合效应的兴趣，同时，由于室温单相多铁性材料BiFeO₃的发现[7]，学术界很快掀起了一股对磁电耦合和多铁性的研究热潮[8]。

近二十年来，关于磁电耦合效应的论文已有数万篇，内容涵盖了新材料探索、新奇效应发现、物理机制研究、应用器件开发、实验表征技术发展等各个方面，已逐渐形成了一门完整的新兴分支学科[9]。

需要指出的是，虽然磁电耦合与多铁性的研究密切相关，但是两者是两个独立的概念，多铁性并不是磁电耦合的必要条件。在笔者看来，无论从基础科学还是实际应用的角度出发，磁电耦合要比多铁性具有更基础、更深刻、更重要的内涵。

伴随着磁电耦合效应的研究，学术界出现了一个新的名词magnetoelectricity [10]。与multiferroicity（多铁性）相对应，magnetoelectricity可以被翻译为“磁电性”，泛指与磁电耦合相关的现象。同时，笔者认为，与电磁学（electromagnetism）相对应，magnetoelectricity也可以被称为“磁电学”，用于指称围绕磁电耦合效应而发展起来的一门新兴分支学科。

磁电子学magnetoelectronics

磁电子学与磁电学虽然仅一字之差，内涵却大不同。

磁电子学来源于magneto（磁）+ electronics（电子学）。半导体电子学是现代电子信息技术的基础，其本质是利用电场调控电荷的运动。在传统电子学中，人们几乎忽略了电子除了电荷之外的另一个基本属性——自旋。直到1988年，法国和德国的两个研究组分别独立地在磁性金属多层膜中发现了巨磁电阻(giant magnetoresistance，GMR)效应，其背后的物理机制使得人们开始意识到电子的输运行为可以与自旋自由度密切相关。

此后，随着越来越多与自旋相关的新效应被发现、被预言、被理解、被利用，一个新的前沿分支学科——自旋电子学（spintronics）蓬勃发展起来。两位最先发现巨磁电阻效应的科学家（法国的Fert和德国的Grünberg）也因自旋电子学的兴起而获得了2007年诺贝尔物理学奖。

由于电子自旋伴随着磁矩，也是物质宏观磁性的主要来源，因此，自旋电子学也被称为磁电子学（magnetoelectronics）[11]。

磁电子学/自旋电子学使得人们认识到，如果能够充分发掘和利用电子的自旋自由度，可以带来超越常规的物理性质。目前，对电子自旋自由度的关注几乎贯穿了凝聚态物理所有的前沿方向。更为重要的是，人们正在基于磁电子学开发新一代低能耗、非易失信息器件和技术，为传统半导体电子学正在面临的巨大瓶颈和挑战提供可能的解决途径。

在电磁学中，一个电流产生的磁场如图3(a)所示。在自旋电子学中，一个自旋极化的电流产生的磁场如图3(b)所示，除了常规电流产生的环形磁场外，还会伴随着一个电子自旋极化导致的有效磁场，其与电流密度、自旋极化方向和自旋极化率等参数有关。

图3（a）常规电流产生的磁场；（b）自旋极化电流产生的磁场

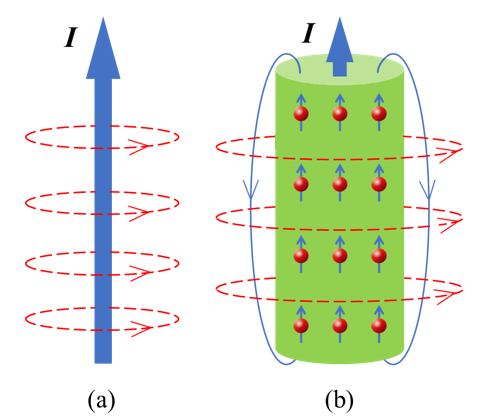
在一个具有强自旋-轨道耦合的介质中通入一个电流I会产生自旋霍尔效应，如图4所示。此时，除了经典电磁学中由电流I产生的磁场外，在介质的边界还存在自旋极化的电子产生的额外磁场。

图4 自旋霍尔效应示意图

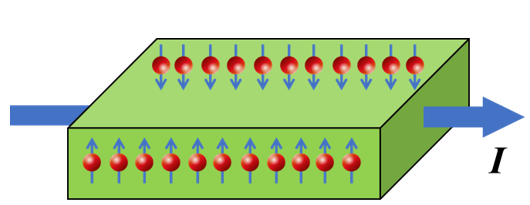
所以，经典麦克斯韦方程组不足以描述存在自旋极化电流和自旋-轨道耦合的情形。

除了自旋极化的电流外，介质中还可以存在无电荷输运的纯自旋流（spin current）。自旋波就是一种典型的纯自旋流。自旋波对应的量子叫磁子（magnon），近年来，对自旋波的基础和应用研究形成了磁电子学的一个亚分支——磁子学（magnonics）[12]。

虽然磁电子学和磁电学在研究内容上存在着一些前沿交叉，两者还是有着很大的区分度，不可混为一谈。磁电子学关注的核心是对电荷和自旋的输运行为的调控和利用，研究对象主要是导体（包括金属和半导体）。磁电学关注的核心是磁场/电场对电极化强度/磁化强度的交叉调控，研究对象主要是绝缘体。

麦克斯韦方程组需要改写吗

如前文所述，我们真实的物质世界要比麦克斯韦方程组描述的情形更丰富、更精彩。既然经典麦克斯韦方程组不足以描述所有介质中的电磁行为，那么，我们需要对其进行改写吗？

为了完整地描述一个介质对外加电场和磁场的响应，我们需要定义一系列系数，如图5所示。电流密度，电极化强度或电位移矢量，磁化强度或磁感应强度是介质对外加电场和磁场的响应结果。

图5介质中可定义的各种系数

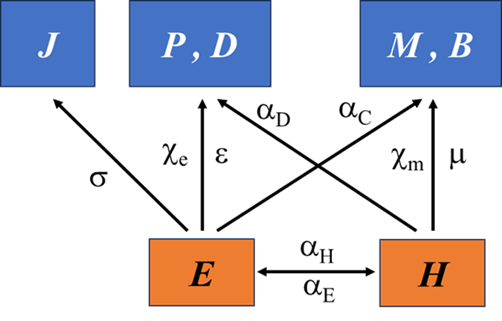
电导率electrical conductivity，，反映了（导体）介质在电场作用下产生电流的能力；

电极化率electric susceptibility，，和

介电率/介电常数dielectric permittivity，，两者都反映了（绝缘）介质对外加电场的响应能力；

磁化率magnetic susceptibility，，和

磁导率magnetic permeability，，两者都反映了介质对外加磁场的响应能力；

正磁电耦合系数direct magnetoelectric coefficient，，反映了外加磁场在介质中诱导电极化强度的能力；

逆磁电耦合系数converse magnetoelectric coefficient，，反映了外加电场在介质中诱导磁化强度的能力；

磁电耦合电场（电压）系数，，反映了介质把外加磁场转化成电场的能力;

磁电耦合磁场系数，，反映了介质把外加电场转化成磁场的能力。

在非各向同性的介质中，这些系数都是二阶张量。相应地，磁电耦合系数也是一个二阶张量，

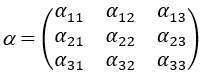
在实际的测量中，磁电耦合电场（电压）系数最容易测量，只需在介质上施加一个磁场，测量在介质两端产生的电压。由此，人们常常用磁电耦合电场（电压）系数来衡量一个材料的磁电耦合强度。

考虑（线性）磁电耦合效应后，介质中的麦克斯韦方程组可以被改写为如下形式：

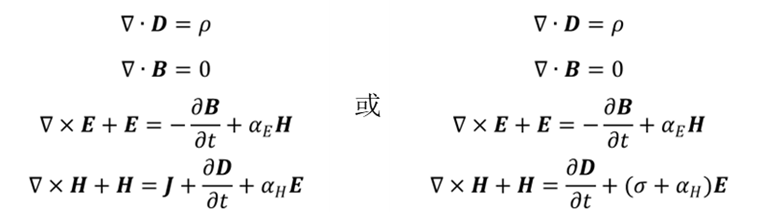
其中，和是介质外部施加的电场和磁场或介质边界产生的电场和磁场。

从上述第三个方程可以看出，有两种途径来产生电场：一是通过变化的磁场（磁通）来产生电场，这正是传统发电机的原理；二是利用磁电耦合效应，通过交变的磁场来产生交变的电场，这是另一种发电机的原理。

从上述第四个方程可以看出，导体和绝缘体在外加电场作用下，分别通过电流（电导率）和磁电耦合来产生磁场。

对于大多数介质，磁电耦合系数和都很小，因此磁电耦合项在麦克斯韦方程组中的贡献可以忽略不记。对于一些特殊介质，磁电耦合项变得不可忽略，甚至可以占据主导地位。例如，对于一些复合磁电耦合材料，在谐振条件下，其磁电耦合系数，即1 Oe的交变磁场可以在1 cm厚的磁电耦合介质两端产生超过1000 V的交变电压！

如果继续考虑自旋极化电流、自旋-轨道耦合等与自旋相关的物理效应，介质中电与磁的交互关联将变得更为复杂，需要引入更多的参数来描述。这也意味着经典麦克斯韦方程组需要不断被修补。

因此，笔者认为，对麦克斯韦方程组进行改写并无太大的意义。在大学物理《电磁学》和《电动力学》课程中，只讲授经典麦克斯韦方程组已足矣。在实际的科学研究和工程应用中，人们只需在麦克斯韦方程组的基础上，额外考虑特殊介质中特定效应带来的新问题。

麦克斯韦方程组因其简洁和对称而被誉为最美的物理学公式之一。如果为了囊括所有可能的情形，让简洁变得冗长，让对称美变得破缺，反而得不偿失，也是物理学家所不能忍的。

电磁学是人类对自然界中宏观电磁现象的归纳和总结，磁电学和磁电子学是对经典电磁学的补充，体现了人类进一步认识自然和改造自然的能力。通过有意识地设计制备新材料、新结构、新器件，使得天然介质中原本微不足道的物理效应得以被呈现、放大和利用，磁电学和磁电子学正在为人类文明带来新知识、新原理、新技术和新应用。

参考文献

[1] P. Curie, Sur Ia symétrie dans les phénomenes physique, symétrie d’un champ électrique et d’unchamp magnétique, J. Phys. 3, 39 (1894).

[2] P. Debye, Remark to some new trials on a magneto-electrical direct effect, Z. Phys. 36, 300 (1926).

[3] E. Dzyaloshinskii, On the magneto-electrical effect in antiferromagnets, Sov. Phys.-JETP 10, 628 (1959).

[4] D. N. Astrov, The magnetoelectric effect in antiferromagnetics, Sov. Phys.- JETP 11, 708 (1960).

[5] H. Schmid, Multiferroic magnetoelectrics, Ferroelectrics 162, 317 (1994).

[6] T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Magnetic control of ferroelectric polarization, Nature 426, 55 (2003).

[7] J. Wang, et al. Epitaxial BiFeO3 multiferroic thin film heterostructures, Science 299, 1719 (2003).

[8] M. Fiebig, Revival of the magnetoelectric effect, J. Phys. D: Appl. Phys. 38, 123 (2005). [9] N. A. Spaldin and R. Ramesh, Advances in magnetoelectric multiferroics, Nature Materials 18, 203 (2019).

[10] Shuai Dong, Hongjun Xiang, and Elbio Dagotto, Magnetoelectricity in multiferroics: a theoretical perspective, National Science Review 6, 629, (2019).

[11] G. A. Prinz, Magnetoelectronics, Science 282, 1660 (1998).

[12] A. Barman et al. The 2021 magnonics roadmap, J. Phys.: Condens. Matter 33, 413001 (2021).

编辑：穆梓

我们是谁：

MatheMagician，中文“数学魔术师”，原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义，也取像魔术一样玩数学的意思。文章内容涵盖互联网，计算机，统计，算法，NLP等前沿的数学及应用领域；也包括魔术思想，流程鉴赏等魔术内容；以及结合二者的数学魔术分享，还有一些思辨性的谈天说地的随笔。希望你能和我一起，既能感性思考又保持理性思维，享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流！

扫描二维码

关注更多精彩

魔术《4 Kings 折纸》的三重境界（四）——魔术效果的突破

视错觉与魔术（二）——橡皮筋的奇迹

你真的懂分数吗？（五）——概率与期望

De Bruijin序列与魔术（四）——De Bruijin序列的拓展结果

这到底是怎么想到的！！！

点击阅读原文，往期精彩不错过！