135. 分发糖果（力扣LeetCode）

135. 分发糖果

题目描述

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

• 每个孩子至少分配到 1 个糖果。
• 相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：

输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：

输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

提示：

• n == ratings.length
• 1 <= n <= 2 * 10⁴
• 0 <= ratings[i] <= 2 * 10⁴

贪心算法

这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，如果两边一起考虑一定会顾此失彼。

先确定右边评分大于左边的情况（也就是从前向后遍历）

此时局部最优：只要右边评分比左边大，右边的孩子就多一个糖果，全局最优：相邻的孩子中，评分高的右孩子获得比左边孩子更多的糖果

局部最优可以推出全局最优。

如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个，所以贪心：candyVec[i] = candyVec[i - 1] + 1

代码如下：

// 从前向后
for (int i = 1; i < ratings.size(); i++) {
    if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
}

如图：

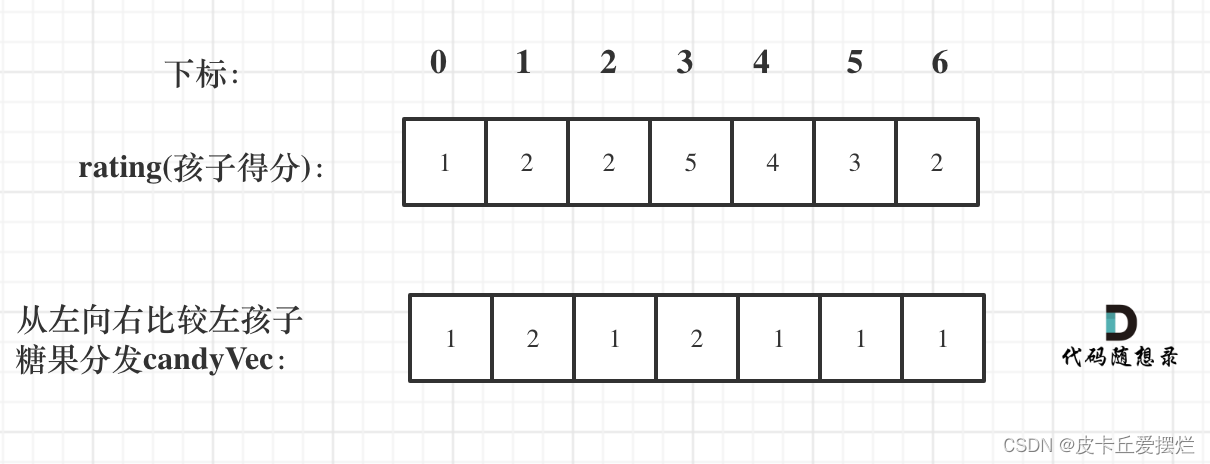
再确定左孩子大于右孩子的情况（从后向前遍历）

遍历顺序这里有同学可能会有疑问，为什么不能从前向后遍历呢？

因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果，所以 要从后向前遍历。

如果从前向后遍历，rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图：

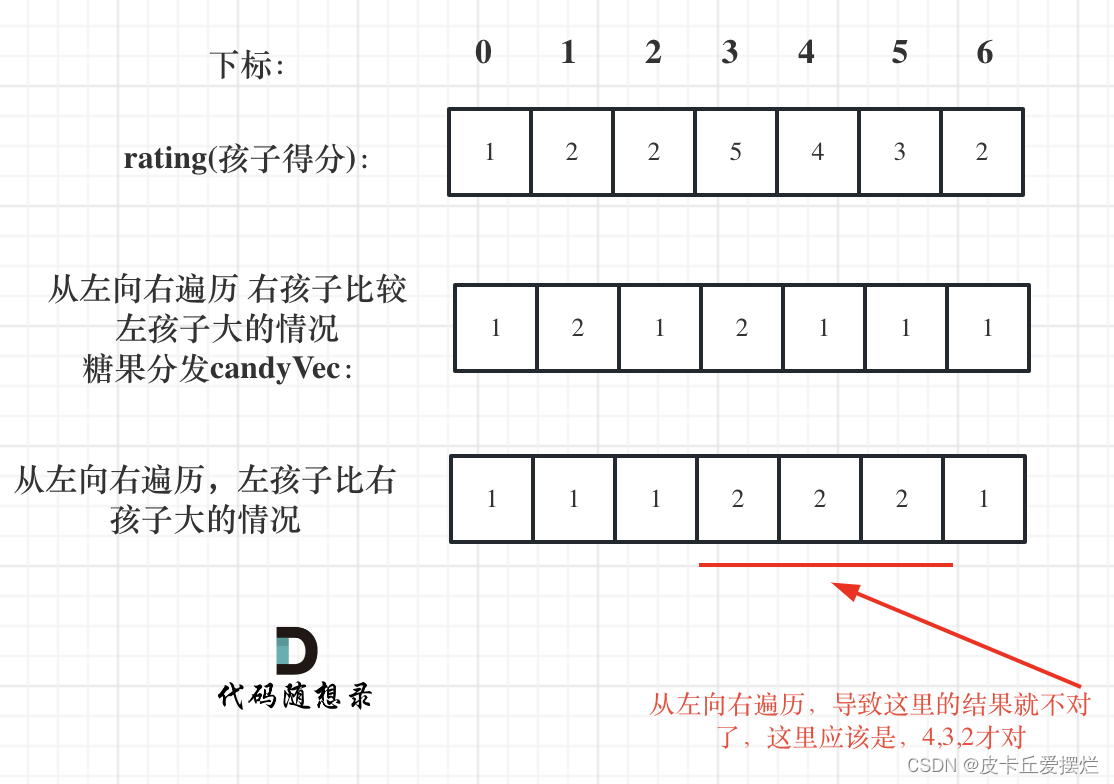
所以确定左孩子大于右孩子的情况一定要从后向前遍历！

如果 ratings[i] > ratings[i + 1]，此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量）。

那么又要贪心了，局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。

局部最优可以推出全局最优。

所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多，也比右边candyVec[i + 1]的糖果多。

如图：

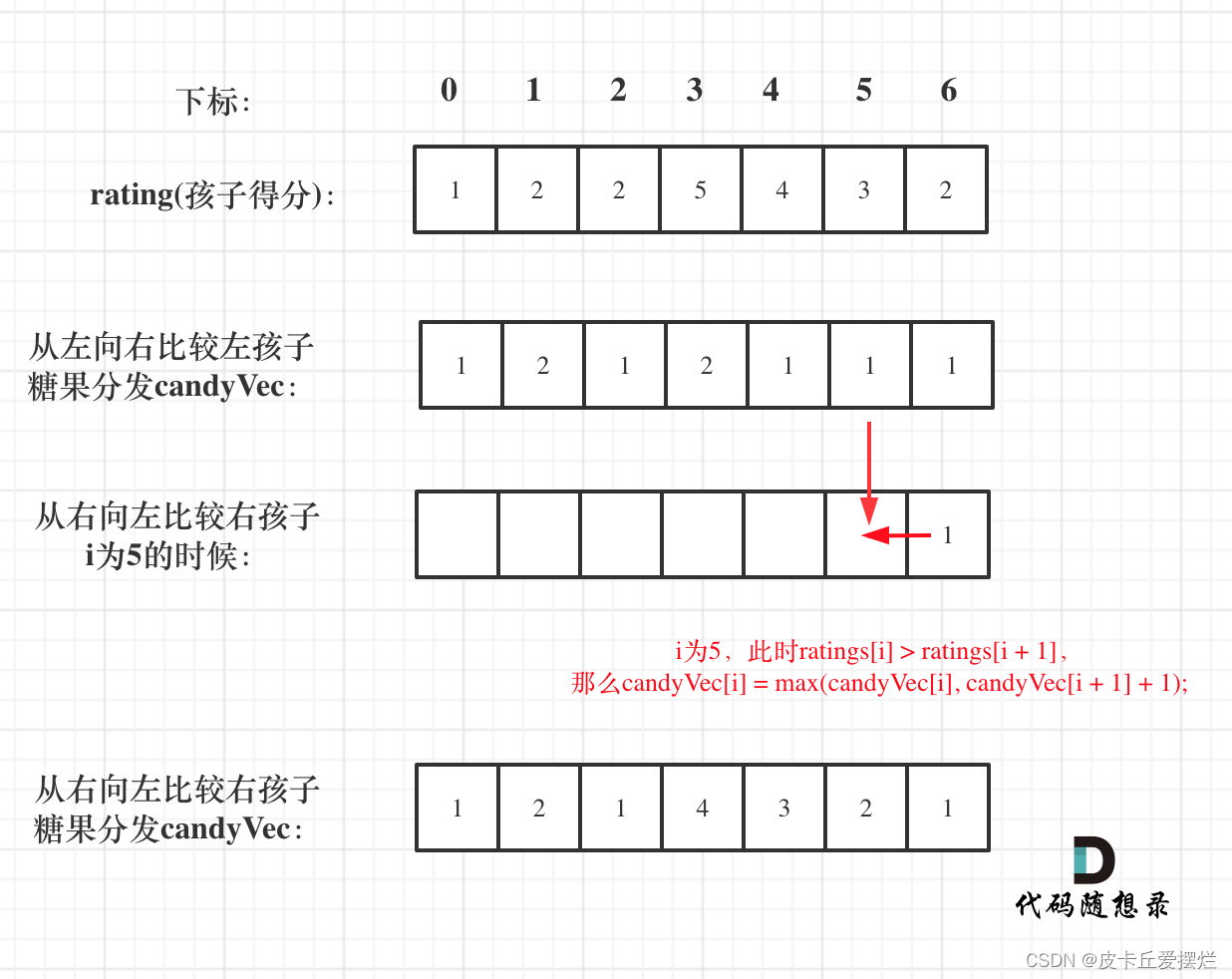
所以该过程代码如下：

// 从后向前
for (int i = ratings.size() - 2; i >= 0; i--) {
    if (ratings[i] > ratings[i + 1] ) {
        candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
    }
}

代码如下

这段代码是解决了一个分发糖果的问题，确保每个孩子根据自己的评分获得适当数量的糖果，同时满足相邻两个孩子之间评分高的孩子获得更多糖果的规则。下面是这段代码的详细注释：

class Solution {
public:
    int candy(vector<int>& ratings) {
        // 1. 初始化一个与评分数组等长的糖果数组，每个孩子先分配1个糖果
        vector<int> sum(ratings.size(),1);
        // 用于记录需要分发的糖果总数
        int num=0;

        // 2. 从左向右遍历，确保每个孩子比其左边评分低的孩子获得更多糖果
        for(int i=0;i<ratings.size()-1;i++)
        {
            // 如果右边孩子的评分比左边的高，则右边孩子的糖果数为左边孩子的糖果数加1
            if(ratings[i+1]>ratings[i])
                sum[i+1]=sum[i]+1;
        }

        // 3. 从右向左遍历，确保每个孩子比其右边评分低的孩子获得更多糖果
        for(int i=ratings.size()-1-1;i>=0;i--)
        {
            // 如果左边孩子的评分比右边的高，且左边孩子目前的糖果数不多于右边孩子，
            // 则左边孩子的糖果数更新为右边孩子的糖果数加1
            if(ratings[i]>ratings[i+1])
                sum[i]=max(sum[i+1]+1,sum[i]);
        }

        // 4. 计算总糖果数
        for(int i=0;i<ratings.size();i++)
            num+=sum[i];
        
        // 返回总糖果数
        return num;
    }
};

这个算法实际上是进行了两次贪心算法的应用：第一次遍历保证了每个孩子都至少比他左边评分低的孩子多一个糖果；第二次遍历则保证了每个孩子都至少比他右边评分低的孩子多一个糖果。这样，就同时满足了题目中的两个条件，而且保证了使用的糖果数目最少。

总结

这在leetcode上是一道困难的题目，其难点就在于贪心的策略，如果在考虑局部的时候想两边兼顾，就会顾此失彼。

那么本题我采用了两次贪心的策略：

• 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
• 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。

这样从局部最优推出了全局最优，即：相邻的孩子中，评分高的孩子获得更多的糖果。