这是根据学校课程、按照《智能控制(第四版)-刘金琨》的书上例题、习题和课后上机实验汇总的本人做过的实验报告和验收代码(含详细解释注释、输出)。所有的截图均来自课本及实验运行结果。
智能控制是一门交叉学科,有一种基于三元论的定义:智能控制IC(Intelligent Control)=自动控制AC(Automatic Control)人工智能AI(Artificial Intelligence)
运筹学OR(Operational Research)。
目录
实验1 对开环/闭环系统的抗扰动性能分析
实验目标
- 设输入电压为0时,扰动信号为Td(s)=1/s,计算和比较开环和闭关两种系统在扰动输入下的稳态误差。
- 验证闭环系统在加入负反馈后的抗扰动性能比开环系统强。
实验背景
- 实验通过电机转速控制系统的框图进行建模和分析。
- 研究开环系统和闭环系统对扰动输入(Td(s))的响应差异,考察其抗扰动性能。
系统模型


- 系统的框图如图所示,包含放大器、转速计等模块。
- 系统参数包括:电枢电阻 (Ra),电机转矩常数 (Km),转动惯量 (J),摩擦系数 (b),反电势常数 (Kb),放大器增益 (Ka),转速计常数 (Kt)。
分析方法
- 使用 MATLAB 编写脚本模拟系统响应。
- 通过生成开环和闭环系统的传递函数,分析系统对扰动的响应曲线。
- 计算开环和闭环系统的稳态输出误差,并比较其数值。
实验过程
开环传递函数:
- 动力学部分:描述电机的机械特性,传递函数
- 电气部分:描述电气驱动和反电势的关系,传递函数
- 通过 feedback() 函数闭合电气部分和动力学部分的环路,将机械特性和电气特性通过负反馈连接。总传递函数
闭环传递函数:
推导中闭环系统加入了负反馈控制,包含控制器(放大器,增益 Ka=54)和反馈路径(转速计,增益 Kt=1和反电势)。闭环系统特性:
- 控制器路径: 控制器增益:
- 反馈路径: 反电势和转速计的组合:
- 电气驱动部分和动力学部分通过串联和反馈闭合,通过 parallel() 和 series() 将反馈部分连接到电机动力学模型,构成闭环传递函数。总传递函数:
- 开环与闭环两者的主要区别在于是否包含控制器和反馈环节。
- 显示初始时间范围和步长的选择:
- 实验仿真时间范围选取为 0~7秒。原因是:从开环系统和闭环系统的阶跃响应图来看,开环系统的响应在 t≈7s 达到稳定状态。闭环系统由于增益大,稳定得更快(t≈0.02s),但实验保持统一时间范围便于比较。
- 在代码中选择步长dt=0.001s,能提供更高精度。
显示扰动信号的体现:
实验中的扰动信号为 Td(s)=1/s,即单位阶跃输入。代码中扰动信号的体现是通过设置单位阶跃输入默认 u(t)=1 ,即 u = ones(size(t)); ,来仿真 Td(s):
- 在开环和闭环系统的传递函数中已有描述这种扰动信号。
- 在numerical_response 函数中,(k/a)项相当于模拟阶跃输入的贡献,默认省略了“*u(i)”,累积到系统状态 x上,从而体现了 Td(s)=1/s 对系统的作用。
程序代码和结果图示
1. 编写matlab代码,完全基于数值计算(显式欧拉法)而不是调用工具箱函数。以下代码通过直接求解微分方程实现响应仿真:
% 定义系统参数
Ra = 1; Km = 10; J = 2; b = 0.5; Kb = 0.1;
Ka = 54; Kt = 1; % 放大器与转速计增益
% 时间轴
T = 0:0.0001:7; % 时间范围,步长为0.001s
% 开环系统计算
% 开环系统传递函数:G_o(s) = -1 / (2s + 1.5)
num_o = -1; den_o = [2 1.5];
sys_o_step = numerical_response(num_o, den_o, T);
% 闭环系统计算
% 闭环系统传递函数:G_c(s) = -1 / (2s + 541.5)
num_c = -1; den_c = [2 541.5];
sys_c_step = numerical_response(num_c, den_c, T);
% 绘制开环响应图
figure; plot(T, sys_o_step, 'r'); grid on;
title('开环系统扰动响应'); xlabel('时间 (s)'); ylabel('\omega_o (rad/s)');
% 绘制闭环响应图
figure; plot(T, sys_c_step, 'b'); grid on;
title('闭环系统扰动响应'); xlabel('时间 (s)'); ylabel('\omega_c (rad/s)');
% 稳态误差计算
ess_open = abs(sys_o_step(end)); % 开环稳态误差
ess_closed = abs(sys_c_step(end)); % 闭环稳态误差
disp(['开环稳态误差: ', num2str(ess_open)]);
disp(['闭环稳态误差: ', num2str(ess_closed)]);
% 辅助函数:基于数值方法计算阶跃响应
function y = numerical_response(num, den, t)
% 获取系统参数
a = den(1); b = den(2);
k = num; % 分子
% 定义时间步长
dt = t(2) - t(1);
n = length(t);
% 初始化输出
y = zeros(1, n);
x = 0; % 初始状态
% 数值计算:递推法
for i = 2:n
dx = (-b/a)*x + (k/a); % 状态更新方程
x = x + dx * dt; % 更新状态
y(i) = x;
end
end
开环稳态误差: 0.66317;闭环稳态误差: 0.0018467

2. 使用工具箱实现,保留公式推导过程,确保简洁性和在复杂系统中的有效性,也避免了人为显示设置时间和步长等初始参数带来的误差:
% 参数定义
Ra = 1; % 电枢电阻
Km = 10; % 电机转矩常数
J = 2; % 转动惯量
b = 0.5; % 摩擦系数
Kb = 0.1; % 反电势常数
Ka = 54; % 放大器增益
Kt = 1; % 转速计常数
% 开环传递函数
num1 = [1]; % 分子
den1 = [J, b]; % 分母
sys1 = tf(num1, den1);
num2 = [Km * Kb/Ra];
den2 = [1];
sys2 = tf(num2, den2);
sys_o = feedback(sys1, sys2);
sys_o = -sys_o; %改变负号
[yo, T] = step(sys_o); % 计算开环系统对阶跃扰动的响应
figure;
plot(T, yo, 'r');
title('开环系统扰动响应');
xlabel('时间 (s)');
ylabel('\omega_o');
grid;
disp(['开环稳态误差: ', num2str(yo(end))]);
% 闭环传递函数
num1 = [1]; % 分子
den1 = [J, b]; % 分母
sys1 = tf(num1, den1);
num2 = [Ka * Kt];
den2 = [1];
sys2 = tf(num2, den2);
num3 = [Kb];
den3 = [1];
sys3 = tf(num3, den3);
num4 = [Km / Ra];
den4 = [1];
sys4 = tf(num4, den4);
sysa = parallel(sys2, sys3);
sysb = series(sysa, sys4);
sys_c = feedback(sys1, sysb);
sys_c = -sys_c;
[yc, T] = step(sys_c); % 计算闭环系统对阶跃扰动的响应
figure;
plot(T, yc, 'b');
title('闭环系统扰动响应');
xlabel('时间 (s)');
ylabel('\omega_c (rad/sec)');
grid;
disp(['闭环稳态误差: ', num2str(yc(end))]);
开环稳态误差: 0.66465;闭环稳态误差: 0.0018411

结论分析
由系统扰动响应时间图和稳态误差的数值可见,闭环系统抗干扰性更强,体现在:
- 稳:系统稳定;
- 准:稳态误差更小;
- 好:动态响应快,超调量小,调节时间短。
不同参数变化对仿真结果的影响分析:
- 电枢电阻 (Ra): 电枢电阻 Ra 影响电机反馈环路的增益。增大 Ra 会减小反馈增益 KmKb/Ra ,使闭环系统的抗扰动能力降低。具体表现为闭环系统的响应变慢,稳态误差增大。而开环系统不受 Ra 的直接影响。
- 电机转矩常数 (Km): Km 直接决定电机输出转矩的大小,增大 Km 会提高反馈路径的增益,从而减小闭环系统的稳态误差,同时加快响应速度。然而,过大的 Km 可能使系统对扰动过于敏感,导致过冲或不稳定。
- 转动惯量 (J): 转动惯量 J 反映了电机的动态特性。增大 J 会减缓系统的动态响应,使开环和闭环系统的响应速度都变慢,达到稳态所需时间延长,但对稳态误差影响较小。
- 摩擦系数 (b): 摩擦系数 b 是系统的阻尼因素,增大 b 会提高系统的稳定性,抑制过冲,并减小稳态误差。然而,过大的 b 会导致闭环系统的动态响应变慢,甚至出现较大的时间延迟。
- 反电势常数 (Kb): Kb 决定了反馈路径的反作用增益。增大 Kb 会提高反馈增益,从而减小闭环系统的稳态误差,加快系统响应速度。但若 Kb 过大,系统可能会变得不稳定。
- 放大器增益 (Ka): Ka 是闭环系统的核心增益参数。增大 Ka 能显著提高反馈强度,减小闭环系统的稳态误差,并加快响应速度。然而,当 Ka 增大到一定程度后,系统可能出现振荡甚至不稳定现象,因此需要合理调节。
- 转速计常数 (Kt): Kt 直接影响反馈路径的增益,增大 Kt 会增强负反馈的效果,从而减小闭环系统的稳态误差,提升动态响应速度。同样,过大的 Kt 可能导致系统不稳定。
理想的参数设置需要在快速响应和稳定性之间取得平衡,避免出现过冲或振荡问题。
知识拓展
该仿真过程除开环与闭环控制系统、负反馈控制原理、传递函数、稳态误差之外,还涉及到了复杂系统模块化组合(并联、串联、反馈)、电机模型、MATLAB 控制系统工具箱。
- 复杂系统模块化组合(并联、串联、反馈)
- 串联:串联表示系统的各部分按顺序连接,输出作为下一级的输入。其总传递函数为各部分传递函数的乘积(如 G(s)=G1(s)⋅G2(s))。在仿真中,串联用于将放大器和电机模型组合成一个整体。
- 并联:并联表示多个系统的输入相同,但输出叠加,其总传递函数为各部分传递函数之和(如 G(s)=G1(s)+G2(s))。在反馈系统中,并联可以用于组合主反馈路径与附加信号(如干扰路径)。
- 反馈:反馈将输出的一部分返回至输入端以修正系统行为。负反馈通过减少偏差提升系统稳定性和抗扰动能力。
- 电机模型
- 模型本身:电机模型基于机械动力学和电路理论。其电枢电路由 Ra,La和反电势 Kbω组成,机械部分由转动惯量 J 和摩擦系数 b 表示。电机的传递函数将输入电压转化为输出转速(或角速度)。
- 放大器增益对反馈路径的作用:放大器增益 Ka 增强了反馈信号的强度,使闭环系统能够更迅速地响应扰动。增大 Ka 可减小稳态误差,但过大的增益可能导致系统振荡或不稳定。
- 转速计的反作用(负反馈增益):转速计测量电机输出转速,并生成与其成比例的反馈信号。其负反馈增益 Kt 能有效抑制扰动输入的影响,提升系统稳定性和动态性能。较高的 Kt 提高抗扰动能力,但过大可能降低系统的灵敏度,甚至引起振荡。
- MATLAB 控制系统工具箱
- tf 函数:用于定义系统的传递函数。
- series 函数:用于计算串联系统的传递函数。
- parallel 函数:用于计算并联系统的传递函数。
- feedback 函数:用于计算反馈系统的传递函数。
- step 函数:用于仿真系统的阶跃响应。
实验2 解释PID控制器及5条专家系统控制原则
解释详见代码注释
课本chap2_1.m
%Expert PID Controller
clear all;
close all;
ts=0.001; %采样时长
sys=tf(5.235e005,[1,87.35,1.047e004,0]); %Plant 传递函数的(增益,【极点(决定动态特性如响应速度和阻尼)】)
dsys=c2d(sys,ts,'z'); %将连续时间系统 sys 离散化,转换为离散时间系统 dsys,使用零阶保持(Zero-order hold)方法进行离散化
[num,den]=tfdata(dsys,'v'); %tfdata 将离散时间传递函数 dsys 的分子和分母提取出来,分别存储在 num 和 den 变量中。'v' 参数表示以向量的形式返回结果。
%初始化
u_1=0;u_2=0;u_3=0; %上一个三个时刻的控制输入,用于计算当前时刻的输出。
y_1=0;y_2=0;y_3=0; %上一个三个时刻的系统输出,用于计算当前时刻的输出。
%需要三个输入输出:比例项是基于当前的误差来计算的,误差越大,控制信号的调整越大。
%微分项是基于误差的变化率来计算的,也就是说,它反映了误差在当前时刻和前一时刻的变化。
%积分项是误差的累积,反映了误差在一段时间内的积累效应。
x=[0,0,0]'; %存储误差的历史状态,x(1) 表示当前的误差 e(k),x(2) 表示误差的差分(变化率,通常用作微分项),x(3) 表示误差的积分(积累值)。
x2_1=0; %x2_1:历史误差差分项的一个变量,表示上一个时刻的 x(2)。
kp=0.6; %比例增益
ki=0.03; %积分增益
kd=0.01; %微分增益
error_1=0; %初始误差,在 PID 控制中用于计算微分项。
for k=1:1:500 %系统将运行 500 次,其中每次迭代对应一个时间步长(ts = 0.001)。每一次循环都代表一个新的采样点。
time(k)=k*ts; %当前时间
r(k)=1.0; %Tracing Step Signal 目标信号(设定点),值始终为 1.0
u(k)=kp*x(1)+kd*x(2)+ki*x(3); %PID Controller PID 控制器的输出是三个项的加权和,调整系统的输入,从而驱动系统输出接近期望的目标。
%Expert control rule
if abs(x(1))>0.8 %Rule1:Unclosed control rule 说明误差的绝对值较大,控制器应按最大(或最小)输出,以便迅速调整,相当于开环控制
u(k)=0.45; %当误差较大时,控制器输出一个较大的值。
elseif abs(x(1))>0.40
u(k)=0.40;
elseif abs(x(1))>0.20
u(k)=0.12;
elseif abs(x(1))>0.01
u(k)=0.10;
end
if x(1)*x(2)>0|(x(2)==0) %Rule2 e*delta(e) 说明误差在朝绝对值增大的方向变化(或常值)
if abs(x(1))>=0.05 %当误差增大时,控制器将加大响应强度,以便快速纠正系统偏差;
u(k)=u_1+2*kp*x(1); %如果 x(1) > 0 且 x(2) > 0,表示误差正朝着增大的方向变化(即误差越来越大)。
else %当误差较小时,减小响应强度,以避免过度调整,只做小幅度调整以消除剩余的小误差。
u(k)=u_1+0.4*kp*x(1); %如果 x(1) < 0 且 x(2) < 0,表示误差正朝着更负的方向变化(即误差越来越负)。
end
end
if (x(1)*x(2)<0&x(2)*x2_1>0)|(x(1)==0) %Rule3 已经朝误差绝对值减小的方向,或者已经平衡,保持控制器输出不变。
u(k)=u(k);
end
if x(1)*x(2)<0&x(2)*x2_1<0 %Rule4 误差已处于极值状态。误差发生了反转(误差的绝对值正在减小),且误差变化的趋势保持一致。
if abs(x(1))>=0.05
u(k)=u_1+2*kp*error_1;
else
u(k)=u_1+0.6*kp*error_1;
end
end
if abs(x(1))<=0.001 %Rule5:Integration separation PI control 误差非常接近零(小于等于 0.001)时,采用 PI 控制(比例 + 积分控制)
u(k)=0.5*x(1)+0.010*x(3); %加入积分,减小稳态误差,控制器会减少输出,以避免系统过度调整并引发不必要的震荡。
end
%Restricting the output of controller 限制了控制器的输出范围在 -10 到 10 之间,防止控制量过大导致系统不稳定。
if u(k)>=10
u(k)=10;
end
if u(k)<=-10
u(k)=-10;
end
%Linear model 离散化的线性模型(由传递函数 dsys 定义),根据前面的输入和输出,计算当前时刻的系统输出 y(k)
y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(1)*u(k)+num(2)*u_1+num(3)*u_2+num(4)*u_3;
error(k)=r(k)-y(k);
%----------Return of parameters------------%
%更新控制器的历史状态
u_3=u_2;u_2=u_1;u_1=u(k); %输入
y_3=y_2;y_2=y_1;y_1=y(k); %输出
x(1)=error(k); % Calculating P
x2_1=x(2);
x(2)=(error(k)-error_1)/ts; % Calculating D
x(3)=x(3)+error(k)*ts; % Calculating I
error_1=error(k); %更新控制器的历史状态
end
figure(1);
%蓝线表示目标信号 r,红线表示系统输出 y。通过比较这两条线的形状可以看到系统输出如何跟踪目标信号。理想情况下,系统输出 y 会尽量接近目标信号 r
plot(time,r,'b',time,y,'r');
xlabel('time(s)');ylabel('r,y');
figure(2);
%误差信号
plot(time,r-y,'r');
xlabel('time(s)');ylabel('error');
实验3 实践模糊控制隶属度函数
解释参数变化的影响
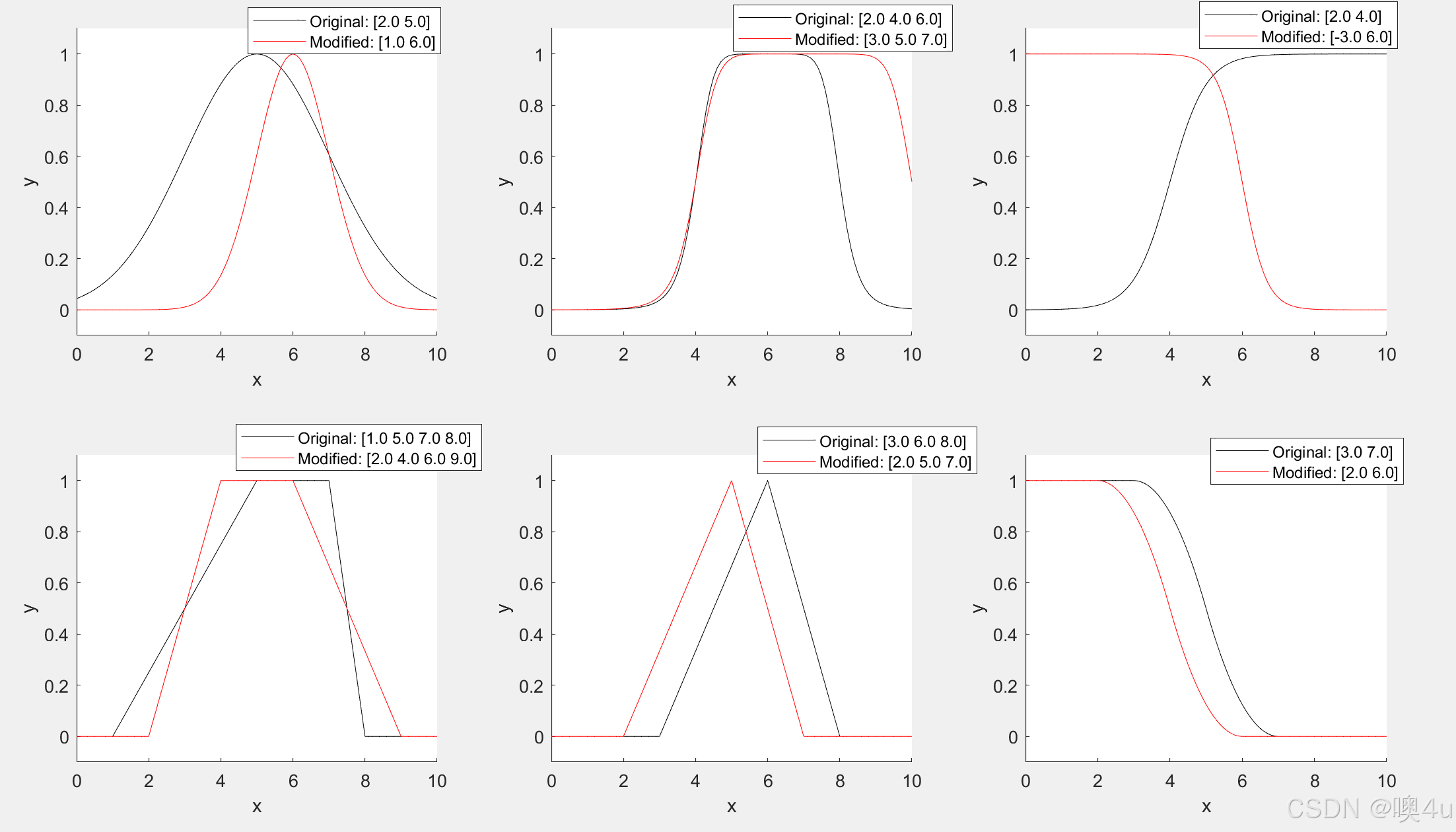
课本例3.5(个人修改,可视化对比参数变化的影响)
解释详见代码注释
% Membership function
clear all;
close all;
% 创建一个2x3的子图布局
figure;
for M = 1:6
subplot(2, 3, M); % 创建子图
x = 0:0.1:10; % 定义x轴数据
hold on; % 保持图像
% 根据M的值选择不同的隶属度函数
if M == 1 % Gaussian membership function 高斯型
params_original = [2 5]; % [峰的宽度 中心]
y = gaussmf(x, params_original);
plot(x, y, 'k', 'DisplayName', sprintf('Original: [%.1f %.1f]', params_original(1), params_original(2)));
% 修改参数并绘制新曲线
params_new = [1 6]; % 修改参数
y_new = gaussmf(x, params_new);
plot(x, y_new, 'r', 'DisplayName', sprintf('Modified: [%.1f %.1f]', params_new(1), params_new(2)));
elseif M == 2 % General Bell membership function 广义钟型
params_original = [2 4 6]; % [宽度 陡峭程度 中心]
y = gbellmf(x, params_original);
plot(x, y, 'k', 'DisplayName', sprintf('Original: [%.1f %.1f %.1f]', params_original(1), params_original(2), params_original(3)));
% 修改参数并绘制新曲线
params_new = [3 5 7]; % 修改参数
y_new = gbellmf(x, params_new);
plot(x, y_new, 'r', 'DisplayName', sprintf('Modified: [%.1f %.1f %.1f]', params_new(1), params_new(2), params_new(3)));
elseif M == 3 % S membership function S形
params_original = [2 4]; % [值决定陡峭程度、正负决定开口方向 0-1的中点横坐标]
y = sigmf(x, params_original);
plot(x, y, 'k', 'DisplayName', sprintf('Original: [%.1f %.1f]', params_original(1), params_original(2)));
% 修改参数并绘制新曲线
params_new = [-3 6]; % 修改参数
y_new = sigmf(x, params_new);
plot(x, y_new, 'r', 'DisplayName', sprintf('Modified: [%.1f %.1f]', params_new(1), params_new(2)));
elseif M == 4 % Trapezoid membership function 梯形
params_original = [1 5 7 8]; % [两条腰的起始、终止横坐标]
y = trapmf(x, params_original);
plot(x, y, 'k', 'DisplayName', sprintf('Original: [%.1f %.1f %.1f %.1f]', params_original(1), params_original(2), params_original(3), params_original(4)));
% 修改参数并绘制新曲线
params_new = [2 4 6 9]; % 修改参数
y_new = trapmf(x, params_new);
plot(x, y_new, 'r', 'DisplayName', sprintf('Modified: [%.1f %.1f %.1f %.1f]', params_new(1), params_new(2), params_new(3), params_new(4)));
elseif M == 5 % Triangle membership function 三角形
params_original = [3 6 8]; % [0-1-0横坐标]
y = trimf(x, params_original);
plot(x, y, 'k', 'DisplayName', sprintf('Original: [%.1f %.1f %.1f]', params_original(1), params_original(2), params_original(3)));
% 修改参数并绘制新曲线
params_new = [2 5 7]; % 修改参数
y_new = trimf(x, params_new);
plot(x, y_new, 'r', 'DisplayName', sprintf('Modified: [%.1f %.1f %.1f]', params_new(1), params_new(2), params_new(3)));
elseif M == 6 % Z membership function Z型
params_original = [3 7]; % [z的形状]
y = zmf(x, params_original);
plot(x, y, 'k', 'DisplayName', sprintf('Original: [%.1f %.1f]', params_original(1), params_original(2)));
% 修改参数并绘制新曲线
params_new = [2 6]; % 修改参数
y_new = zmf(x, params_new);
plot(x, y_new, 'r', 'DisplayName', sprintf('Modified: [%.1f %.1f]', params_new(1), params_new(2)));
end
% 设置图表属性
xlabel('x');
ylabel('y');
legend;
axis([0 10 -0.1 1.1]); % 统一设置坐标轴范围
hold off; % 关闭图像保持
end
设计根据年龄“年轻”“年老”的隶属度函数
课本习题3-1
clear all;
close all;
% 已知年老的隶属函数
for k1 = 1:1:2001 % 论域[0,200] 0.1为步长
x1(k1) = (k1-1)*0.1;
if x1(k1)>=50&x1(k1)<=70
y1(k1)=( x1(k1) -50)/20;
elseif x1(k1)>70
y1(k1) = 1.0;
else
y1(k1) = 0;
end
end
% 已知年轻的隶属函数
for k = 1:1:2001
x(k) = (k-1)*0.1;
if x(k)>=0&x(k)<=25;
y(k) = 1.0;
elseif x(k)>25&x(k)<=70
y(k)=(70 - x(k))/45;
else
y(k) = 0;
end
end
% 很年轻
for k2 = 1:1:2001
x2(k2) = (k2-1)*0.1;
if x2(k2)>=0&x2(k2)<=25;
y2(k2) = 1.0;
elseif x2(k2)>25&x2(k2)<=70
y2(k2)=((70 - x2(k2))/45)^2; % "很":语气算子:平方
else
y2(k2) = 0;
end
end
% 不老也不年轻 "非老"交"非年轻" 范围:[25, 70]岁
%在0到25岁之间,隶属度为0(完全不属于"不老不年轻”)。
%在25到50岁之间,隶属度逐渐增大,体现从"年轻"到"不老不年轻”的过渡。1-Vy
%在50岁到60岁之间,隶属度=1。
%在60到70岁之间,隶属度逐渐减小,体现从"不老不年轻"到"老"的过渡。1-Vo
%在70岁以上,隶属度为0(完全不属于"不老不年轻”)。
for k3 = 1:1:2001
x3(k3) = (k3-1)*0.1;
if x3(k3) >= 25 && x3(k3) <= 50
y3(k3) = 1 - (70 - x3(k3)) / 45; % 从不年轻过渡到不老
elseif x3(k3) > 50 && x3(k3) <= 60
y3(k3) = 1; % 隶属度为1,表示完全处于"不老不年轻"区域
elseif x3(k3) > 60 && x3(k3) <= 70
y3(k3) = 1 - (x3(k3) - 50) / 20; % 从不老过渡到年老
else
y3(k3) = 0; % 不属于该区间
end
end
% 使用subplot将4个图放在同一图中
figure;
% 第一个子图
subplot(2, 2, 1);
plot(x, y, 'k');
xlabel('x Years');
ylabel('年轻 Y');
title('年轻');
% 第二个子图
subplot(2, 2, 2);
plot(x1, y1, 'k');
xlabel('x Years');
ylabel('年老 O');
title('年老');
% 第三个子图
subplot(2, 2, 3);
plot(x2, y2, 'k');
xlabel('x Years');
ylabel('很年轻 W');
title('很年轻');
% 第四个子图
subplot(2, 2, 4);
plot(x3, y3, 'k');
xlabel('x Years');
ylabel('不老也不年轻 V');
title('不老也不年轻');

实验4 模糊控制器设计实例
水箱模糊控制 (单变量输入、单变量输出)
实验目标
- 学习Matlab fuzzy工具箱设计模糊控制器
- 完成教材P34页的水箱控制案列
实验题目
以水位的模糊控制为例,设有一个水箱,通过调节阀门可向内注水和向外抽水,设计一个模糊控制器,通过调节阀门将水位稳定在固定点附近,按照日常的操作经验,可以得到基本的控制规则为:
“若水位高于O点,则向外排水,差值越大,排水越快”;
“若水位低于O点,则向内注水,差值越大,注水越快”。
系统模型

- 选择液位差为e,分为5个模糊集:NB:负大 NS:负小 Z:零 PS:正小 PB:正大,将偏差e变化分为7个等级:-3,-2,-1,0,1,2,3。得到水位模糊变化表。
- 控制量u,分为5个模糊集:NB:负大 NS:负小 Z:零 PS:正小 PB:正大,将u变化分为9个等级:-4,-3,-2,-1,0,1,2,3,4。得到控制量模糊划分表。

- 模糊规则的描述:若e负大,则u负大;若e负小,则u负小;若e为零,则u为零;若e正小,则u正小;若e正大,则u正大。

- 求模糊关系
- 模糊决策
- 控制量的反模糊化


实验过程
使用fuzzy工具箱直接实现
- 在命令行中输入fuzzy打开工具箱。
- 输入输出的建立

-
Range:论域
-
Edit-Add MFs…:添加模糊子集(如负大、正小…)
-
Type:隶属度函数种类
-
输出与输入同理
-
- 添加规则(If…Then…)

-
Edit-Rules…
-
- 推理设计
-
一般情况下都使用默认的方法(与:取小;或:取大;…)
-
- 查看控制平面

-
View-Surface
-
或者 View-rules可以查看规则(控制输入和其对应的输出值)
-
使用代码编程调用实现
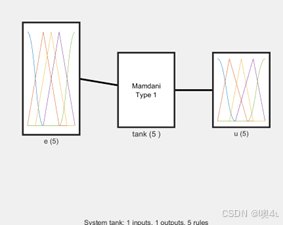
首先创建一个名为“fuzz_tank”的模糊推理系统。接着,定义了入变量“e”(表示误差)和输出变量“u”(表示控制量),并分别为它们添加了五个隶属函数,涵盖从负大到正大的不同模糊状态。随后,通过设定规则库,将输入和输出的模糊集合进行对应,形成基本的控制规则。代码选择了中心矩法作为去模糊化方法,并将模糊系统保存为文件后重新读取,以确保配置正确。之后,绘制模糊系统的结构图以及输入输出的隶属函数图,方便可视化理解。如果设置标志变量,代码还会显示规则库并进行动态仿真。最后,通过对一系列误差值进行模糊推理,计算并输出相应的控制量,从而实现根据不同误差自动调整控制输出,达到有效控制水箱液位的目的。
%Fuzzy Control for water tank
clear all;
close all;
a=newfis('fuzz_tank');
a=addvar(a,'input','e',[-3,3]); %Parameter e
a=addmf(a,'input',1,'NB','zmf',[-3,-1]);
a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);
a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);
a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);
a=addmf(a,'input',1,'PB','smf',[1,3]);
a=addvar(a,'output','u',[-4,4]); %Parameter u
a=addmf(a,'output',1,'NB','zmf',[-4,-1]);
a=addmf(a,'output',1,'NS','trimf',[-4,-2,1]);
a=addmf(a,'output',1,'Z','trimf',[-2,0,2]);
a=addmf(a,'output',1,'PS','trimf',[-1,2,4]);
a=addmf(a,'output',1,'PB','smf',[1,4]);
rulelist=[1 1 1 1; %Edit rule base
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];
a=addrule(a,rulelist);
a1=setfis(a,'DefuzzMethod','mom'); %Defuzzy
writefis(a1,'tank'); %Save to fuzzy file "tank.fis"
a2=readfis('tank');
figure(1);
plotfis(a2);
figure(2);
plotmf(a,'input',1);
figure(3);
plotmf(a,'output',1);
flag=1;
if flag==1
showrule(a) %Show fuzzy rule base
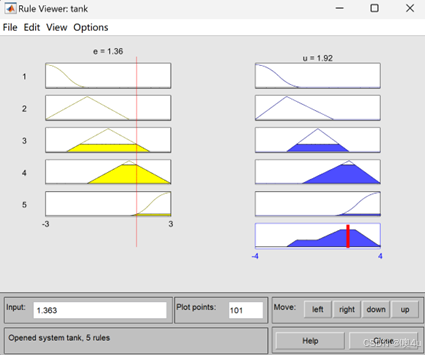
ruleview('tank'); %Dynamic Simulation
end
disp('-------------------------------------------------------');
disp(' fuzzy controller table:e=[-3,+3],u=[-4,+4] ');
disp('-------------------------------------------------------');
for i=1:1:7
e(i)=i-4;
Ulist(i)=evalfis([e(i)],a2);
end
Ulist=round(Ulist)
e=-3; % Error
u=evalfis([e],a2) %Using fuzzy inference
ans =
5×34 char 数组
'1. If (e is NB) then (u is NB) (1)'
'2. If (e is NS) then (u is NS) (1)'
'3. If (e is Z) then (u is Z) (1) '
'4. If (e is PS) then (u is PS) (1)'
'5. If (e is PB) then (u is PB) (1)'
-------------------------------------------------------
fuzzy controller table:e=[-3,+3],u=[-4,+4]
-------------------------------------------------------
Ulist =
-4 -2 -2 0 2 2 4
u =
-4



知识拓展
MATLAB的模糊控制工具箱(Fuzzy Logic Toolbox)提供了五种常用的解模糊化方法:
- 重心法(Centroid)
- 原理:计算模糊集合的重心,即所有可能输出值的加权平均。
- 优点:考虑了整个模糊区域的信息,结果平滑。
- 应用:最常用的解模糊方法,适用于大多数控制系统。
- 双分割法(Bisector)
- 原理:找到一个值,使得模糊集合在该值左侧和右侧的面积相等。
- 优点:能够平衡模糊集合的左右部分,适合对对称性有要求的系统。
- 应用:用于需要对称处理的控制场景。
- 最大值的平均(Mean of Maximum, MOM)
- 原理:取模糊集合中所有达到最大隶属度的输出值的平均。
- 优点:计算简单,适合快速决策。
- 应用:适用于对响应速度要求较高的控制系统。
- 最大值中的最小值(Smallest of Maximum, SOM)
- 原理:在所有达到最大隶属度的输出值中,选择最小的那个值。
- 优点:保守地选择最小输出,避免过大调整。
- 应用:适用于需要限制输出变化范围的场景。
- 最大值中的最大值(Largest of Maximum, LOM)
- 原理:在所有达到最大隶属度的输出值中,选择最大的那个值。
- 优点:积极地选择最大输出,增强系统响应。
- 应用:适用于需要快速反应和较大调整的控制系统。
模糊控制器设计步骤
课本chap4_2.m,表4-5、4-6
实验目标
了解模糊控制器的设计步骤,掌握模糊模型结构的建立、模糊数据库的构建、模糊规则库的设计、模糊推理过程以及解模糊的方法。
实验题目
“模糊控制位置追踪”:被控对象为G(s)=400/(s^2+500s) 。
系统模型
本实验设计的模糊控制器用于控制一个二阶系统,其中系统的输出为位置,输入为控制量。控制器通过调整控制量(u)以减小位置误差(e)及其变化率(ec),实现对系统的精确控制。
模糊控制器最简单的实现方法是将一系列模糊控制规则离线转化为一个查询表(又称为控制表),存储在计算机中供在线控制时使用。这种模糊控制器结构简单,使用方便,是最基本的一种形式。

实验过程
1.模糊控制器的结构:单变量二位模糊控制器。
2.定义输入、输出模糊集(数据库):对误差e、误差变化率ec、控制输入u的设计如下:
2.1控制对象
- 输出变量(位置):反映系统的当前位置。
- 输入变量:
- 误差(e):参考输入信号与实际输出位置之间的差值。
- 误差变化率(ec):误差随时间的变化趋势。
2.2模糊控制器输入输出
- 输入:
- 误差(e):论域 [-0.3, 0.3],划分为七个模糊子集:NB、NM、NS、Z、PS、PM、PB。
- 误差变化率(ec):论域 [-0.3, 0.3],同样划分为七个模糊子集,与误差变量一致。
- 输出:
- 控制量(u):论域 [-30, 30],划分为七个模糊子集:NB、NM、NS、Z、PS、PM、PB。

3.定义输入输出隶属函数:对模糊变量赋值,确定论域内元素对模糊变量的隶属度。
4.建立模糊控制规则(规则库):基于专家经验和系统动态特性,在条件语句中,e、ec、u对不同的被控对象有不同的意义。if e is [e级别] and ec is [ec级别] then u is [u级别]。
5.建立模糊控制表:模糊控制集合U=u1+u2+...+u49,每个模糊语句之间是“或”的关系。
,每个模糊语句之间是“或”的关系。

6.模糊推理
- 1.规则匹配:将当前传感器获得的信息分别带入所属的隶属函数求隶属度;
- 2.规则触发:将规则匹配的结果带入模糊控制表,触发隶属度不为0处的规则;
- 3.规则前提推理:同一条规则内,前提之间取“与”得到规则结论,隶属度值取小运算;
- 4.模糊系统总输出:模糊系统总的可信度为各条规则可信度推理结果的并集(取大)。
7.反模糊化
以最大隶属度平均法(lom/som)为例:将6.4中得到的最大隶属度带回其隶属函数,得到控制变量的精确输出值。
代码实现:
%Fuzzy Controller Design
clear all;
close all;
a=newfis('fuzzf');
%% 确定控制对象及输入输出变量 (模糊数据库)
% 该系统是一个二阶系统,输出为位置,输入为控制量。设计模糊控制器的第一步是确定模糊控制器的输入和输出变量。
% 选择了误差 (e) 和误差变化率 (ec) 作为模糊控制器的两个输入变量(input),输出变量为控制量 (u)。
% 分别定义模糊子集(本代码中都是7个)和隶属函数(模糊隶属函数的设计需要根据被控对象的特性、期望控制精度和经验知识来选择与调试。)
a=addvar(a,'input','e',[-0.3,0.3]); %Parameter e 参考输入信号与实际输出位置之间的差 论域[-0.3, 0.3]
a=addmf(a,'input',1,'NB','zmf',[-0.3,-0.1]);
a=addmf(a,'input',1,'NM','trimf',[-0.3,-0.2,0]);
a=addmf(a,'input',1,'NS','trimf',[-0.3,-0.1,0.1]);
a=addmf(a,'input',1,'Z','trimf',[-0.2,0,0.2]);
a=addmf(a,'input',1,'PS','trimf',[-0.1,0.1,0.3]);
a=addmf(a,'input',1,'PM','trimf',[0,0.2,0.3]);
a=addmf(a,'input',1,'PB','smf',[0.1,0.3]);
a=addvar(a,'input','ec',[-0.3,0.3]); %Parameter ec 表征误差随时间变化的趋势 论域[-0.3, 0.3]
a=addmf(a,'input',2,'NB','zmf',[-0.3,-0.1]);
a=addmf(a,'input',2,'NM','trimf',[-0.3,-0.2,0]);
a=addmf(a,'input',2,'NS','trimf',[-0.3,-0.1,0.1]);
a=addmf(a,'input',2,'Z','trimf',[-0.2,0,0.2]);
a=addmf(a,'input',2,'PS','trimf',[-0.1,0.1,0.3]);
a=addmf(a,'input',2,'PM','trimf',[0,0.2,0.3]);
a=addmf(a,'input',2,'PB','smf',[0.1,0.3]);
a=addvar(a,'output','u',[-30,30]); %Parameter u 控制输出 论域[-30, 30]
a=addmf(a,'output',1,'NB','zmf',[-30,-30]);
a=addmf(a,'output',1,'NM','trimf',[-30,-20,0]);
a=addmf(a,'output',1,'NS','trimf',[-30,-10,10]);
a=addmf(a,'output',1,'Z','trimf',[-20,0,20]);
a=addmf(a,'output',1,'PS','trimf',[-10,10,30]);
a=addmf(a,'output',1,'PM','trimf',[0,20,30]);
a=addmf(a,'output',1,'PB','smf',[10,30]);
%% 建立模糊规则库
% 规则库的设计过程通常借鉴专家经验、被控系统的动态特性以及实际调试过程。
% 每一条规则的格式为 [e级别 ec级别 u级别 1(规则的权重) 1(also,若是2就是or)]
rulelist=[1 1 1 1 1; %Edit rule base 定义了 49 条模糊控制规则。
1 2 1 1 1;% 如该条规则为:if e is NB and ec is NM then u is NB
1 3 2 1 1;
1 4 2 1 1;
1 5 3 1 1;
1 6 3 1 1;
1 7 4 1 1;
2 1 1 1 1;
2 2 2 1 1;
2 3 2 1 1;
2 4 3 1 1;
2 5 3 1 1;
2 6 4 1 1;
2 7 5 1 1;
3 1 2 1 1;
3 2 2 1 1;
3 3 3 1 1;
3 4 3 1 1;
3 5 4 1 1;
3 6 5 1 1;
3 7 5 1 1;
4 1 2 1 1;
4 2 3 1 1;
4 3 3 1 1;
4 4 4 1 1;
4 5 5 1 1;
4 6 5 1 1;
4 7 6 1 1;
5 1 3 1 1;
5 2 3 1 1;
5 3 4 1 1;
5 4 5 1 1;
5 5 5 1 1;
5 6 6 1 1;
5 7 6 1 1;
6 1 3 1 1;
6 2 4 1 1;
6 3 5 1 1;
6 4 5 1 1;
6 5 6 1 1;
6 6 6 1 1;
6 7 7 1 1;
7 1 4 1 1;
7 2 5 1 1;
7 3 5 1 1;
7 4 6 1 1;
7 5 6 1 1;
7 6 7 1 1;
7 7 7 1 1];
a=addrule(a,rulelist);
%showrule(a) % Show fuzzy rule base
%% 推理与解模糊
a1=setfis(a,'DefuzzMethod','mom');
% Defuzzy 模糊方法为 "mom"(中点平均法,mean of maxima)
% 常见的还有重心法(centroid)、最大隶属度平均法(lom、som)、加权平均法
writefis(a1,'fuzzf'); % save to fuzzy file "fuzz.fis" which can be
% simulated with fuzzy tool
a2=readfis('fuzzf');
disp('-------------------------------------------------------');
disp(' fuzzy controller table:e=[-3,+3],ec=[-3,+3] ');
disp('-------------------------------------------------------');
%% 验证与调试
% 通过 evalfis 对从 [-4,-4] 到 [+3,+3] 范围的 e, ec 样本点进行模糊推理输出 Ulist,
% 这是一种快速检查规则库合理性的方法。
% 通过对 Ulist 的检查、仿真结果的观察(在 Simulink 中运行 chap4_3.mdl),
% 可以判断设计的模糊控制器对输入误差及误差变化有何种响应,并根据实际控制效果进行微调。
Ulist=zeros(7,7);
for i=1:7
for j=1:7
e(i)=-4+i;
ec(j)=-4+j;
Ulist(i,j)=evalfis([e(i),ec(j)],a2);
end
end
Ulist=ceil(Ulist)
%行索引 i 对应误差 e,从上到下为 e = -3, -2, -1, 0, 1, 2, 3
%列索引 j 对应误差变化率 ec,从左到右为 ec = -3, -2, -1, 0, 1, 2, 3
figure(1);
plotfis(a2);
figure(2);
plotmf(a,'input',1);
figure(3);
plotmf(a,'input',2);
figure(4);
plotmf(a,'output',1);

洗衣机模糊控制(双变量输入、单变量输出)
课本chap4_6.m
%Fuzzy Control for washer
clear all;
close all;
a=newfis('fuzz_wash');
a=addvar(a,'input','x',[0,100]); %Fuzzy Stain
a=addmf(a,'input',1,'SD','trimf',[0,0,50]);
a=addmf(a,'input',1,'MD','trimf',[0,50,100]);
a=addmf(a,'input',1,'LD','trimf',[50,100,100]);
a=addvar(a,'input','y',[0,100]); %Fuzzy Axunge
a=addmf(a,'input',2,'NG','trimf',[0,0,50]);
a=addmf(a,'input',2,'MG','trimf',[0,50,100]);
a=addmf(a,'input',2,'LG','trimf',[50,100,100]);
a=addvar(a,'output','z',[0,60]); %Fuzzy Time
a=addmf(a,'output',1,'VS','trimf',[0,0,10]);
a=addmf(a,'output',1,'S','trimf',[0,10,25]);
a=addmf(a,'output',1,'M','trimf',[10,25,40]);
a=addmf(a,'output',1,'L','trimf',[25,40,60]);
a=addmf(a,'output',1,'VL','trimf',[40,60,60]);
rulelist=[1 1 1 1 1; %Edit rule base
1 2 3 1 1;
1 3 4 1 1;
2 1 2 1 1;
2 2 3 1 1;
2 3 4 1 1;
3 1 3 1 1;
3 2 4 1 1;
3 3 5 1 1];
a=addrule(a,rulelist);
showrule(a) %Show fuzzy rule base
a1=setfis(a,'DefuzzMethod','mom'); %Defuzzy
writefis(a1,'wash'); %Save to fuzzy file "wash.fis"
a2=readfis('wash');
figure(1);
plotfis(a2);
figure(2);
plotmf(a,'input',1);
figure(3);
plotmf(a,'input',2);
figure(4);
plotmf(a,'output',1);
ruleview('wash'); %Dynamic Simulation
x=60;
y=70;
z=evalfis([x,y],a2) %Using fuzzy inference实验5 神经网络控制
BP网络逼近仿真

课本chap7_1.m
这是一个2-6-1的BP网络,用于识别和拟合一个非线性系统的输出。
%BP identification
clear all;
close all;
%% 初始化
xite=0.50; %学习率(学习步长)为0.50
alfa=0.05; %动量因子为0.05,用于加速收敛并避免陷入局部最小值
w2=rands(6,1); %随机初始化输出层权重向量 w2,长度为6
w2_1=w2;w2_2=w2_1; %创建权重 w2 的两个历史副本,用于动量项的计算
w1=rands(2,6); %随机初始化隐藏层权重矩阵 w1
w1_1=w1;w1_2=w1; %创建权重 w1 的两个历史副本
dw1=0*w1; %初始化为0矩阵,用于存储在每次迭代中,输入层到隐藏层权重 w1 的更新量
x=[0,0]'; %初始化输入向量 x 为零向量
u_1=0; % 初始化前一时刻的输入 u_1 和输出 y_1 为零
y_1=0;
I=[0,0,0,0,0,0]'; %初始化为6维零向量,用于存储每个隐藏神经元的输入、输出和导数
Iout=[0,0,0,0,0,0]';
FI=[0,0,0,0,0,0]';
%% 设置时间步长为0.001秒,迭代1000次
ts=0.001;
for k=1:1:1000
time(k)=k*ts;
u(k)=0.50*sin(3*2*pi*k*ts); %生成输入信号 u(k),为频率为3 Hz的正弦波,振幅为0.5
y(k)=u_1^3+y_1/(1+y_1^2); %定义目标输出 y(k),基于前一时刻的输入 u_1 和输出 y_1,体现系统的非线性特性
for j=1:1:6 %遍历6个隐藏神经元
I(j)=x'*w1(:,j); %计算每个隐藏神经元的加权输入
Iout(j)=1/(1+exp(-I(j))); %通过Sigmoid激活函数计算隐藏层输出
end
yn(k)=w2'*Iout; %计算神经网络的输出 yn(k),即输出层的加权和 Output of NNI networks
%% 计算误差并更新输出层权重
e(k)=y(k)-yn(k); %目标输出与神经网络输出的差值 Error calculation
w2=w2_1+(xite*e(k))*Iout+alfa*(w2_1-w2_2); %上一时刻的w2+基于误差和隐藏层输出的权重更新项+动量项(利用权重的历史变化来调整当前更新,增加训练的稳定性和速度)
%% 计算隐藏层导数并更新隐藏层权重
for j=1:1:6
FI(j)=exp(-I(j))/(1+exp(-I(j)))^2; %计算Sigmoid函数的导数,用于反向传播中的梯度计算
end
for i=1:1:2 %双重循环,遍历输入层和隐藏层的所有连接
for j=1:1:6
dw1(i,j)=e(k)*xite*FI(j)*w2(j)*x(i); %计算隐藏层权重的更新量,基于误差、学习率、Sigmoid导数、输出层权重和输入值
end
end
w1=w1_1+dw1+alfa*(w1_1-w1_2); %更新隐藏层权重 w1,包括权重更新量和动量项
%% 计算雅可比矩阵(Jacobian)
%%%%%%%%%%%%%%Jacobian%%%%%%%%%%%%%%%%向量值函数的所有一阶偏导数构成的矩阵,反映了输出 yn 对输入 x(1)(即 u(k))的敏感度
yu=0; %初始化雅可比矩阵的一个元素
for j=1:1:6
yu=yu+w2(j)*w1(1,j)*FI(j); %计算雅可比矩阵的值,累加了所有隐藏神经元的输出权重 w2(j) 与输入权重 w1(1,j) 以及激活函数的导数 FI(j) 的乘积。
end
dyu(k)=yu;
x(1)=u(k);
x(2)=y(k);
w1_2=w1_1;w1_1=w1;
w2_2=w2_1;w2_1=w2;
u_1=u(k);
y_1=y(k);
end
figure(1); %绘制目标输出 y(红色)和神经网络输出 yn(蓝色)随时间的变化
plot(time,y,'r',time,yn,'b');
xlabel('times');ylabel('y and yn');
figure(2); %绘制误差 y - yn 随时间的变化
plot(time,y-yn,'r');
xlabel('times');ylabel('error');
figure(3); %绘制雅可比值 dyu 随时间的变化
plot(time,dyu);
xlabel('times');ylabel('dyu');


课本7_2a.m(训练) 7_2b.m(测试)
%BP Training for MIMO and Multi-samples
clear all;
close all;
%% 参数初始化 3-6-2
xite = 0.50; % 学习率
alfa = 0.05; % 动量因子
w2 = rands(6,2); % 隐藏层到输出层的权重矩阵(6个隐藏神经元,2个输出神经元)
w2_1 = w2; w2_2 = w2_1; % 保存上一次的权重值,用于动量更新
w1 = rands(3,6); % 输入层到隐藏层的权重矩阵(3个输入,6个隐藏神经元)
w1_1 = w1; w1_2 = w1_1; % 同样保存上一次的权重值
dw1 = 0 * w1; % 初始化权重更新量矩阵为零
I=[0,0,0,0,0,0]';
Iout=[0,0,0,0,0,0]';
FI=[0,0,0,0,0,0]';
OUT = 2; % 输出层的神经元数量
k = 0; % 训练的次数
E = 1.0; % 初始误差
NS = 3; % 训练样本数
%% 反向传播训练过程
while E>=1e-020 %直到误差𝐸小于 1e-020,停止训练
k=k+1;
times(k)=k;
for s=1:1:NS %MIMO Samples
xs=[1,0,0; %样本输入包含了 3 个样本,每个样本有 3 个输入
0,1,0;
0,0,1]; %Ideal Input
ys=[1,0; %理想输出每个样本对应一个 2 维的输出
0,0.5;
0,1]; %Ideal Output
x=xs(s,:);
%隐藏层计算
for j=1:1:6
I(j)=x*w1(:,j); % 计算每个隐藏层神经元的输入
Iout(j)=1/(1+exp(-I(j))); % 使用 sigmoid 激活函数
end
%输出层计算
yl = w2' * Iout; % 计算输出层的输出
yl = yl'; % 转置使其符合输出形式
%输出误差计算
el=0;
y=ys(s,:); % 获取目标输出
for l=1:1:OUT
el=el+0.5*(y(l)-yl(l))^2; % 计算输出误差(均方误差)Output error
end
es(s)=el;
%总误差计算
E=0;
if s==NS
for s=1:1:NS
E=E+es(s); % 计算总误差
end
end
ey=y-yl;
w2 = w2_1 + xite * Iout * ey + alfa * (w2_1 - w2_2); % 使用梯度下降法更新 w2,并加上动量项 alfa * (w2_1 - w2_2)。
for j = 1:1:6
S = 1 / (1 + exp(-I(j))); % 计算sigmoid函数的输出
FI(j) = S * (1 - S); % 计算sigmoid函数的导数
end
%计算并更新 w1(输入层到隐藏层的权重),根据误差反向传播。
for i=1:1:3
for j=1:1:6
dw1(i,j)=xite*FI(j)*x(i)*(ey(1)*w2(j,1)+ey(2)*w2(j,2));
end
end
w1=w1_1+dw1+alfa*(w1_1-w1_2);
w1_2=w1_1;w1_1=w1;
w2_2=w2_1;w2_1=w2;
end %End of for
Ek(k)=E;
end %End of while
%% 绘制误差曲线
figure(1);
plot(times,Ek,'r');
xlabel('k');ylabel('E');
save wfile w1 w2;%Test BP
clear all;
load wfile w1 w2;
%N Samples
x=[0.970,0.001,0.001;
0.000,0.980,0.000;
0.002,0.000,1.040;
0.500,0.500,0.500;
1.000,0.000,0.000;
0.000,1.000,0.000;
0.000,0.000,1.000];
for i=1:1:7
for j=1:1:6
I(i,j)=x(i,:)*w1(:,j);
Iout(i,j)=1/(1+exp(-I(i,j)));
end
end
y=w2'*Iout';
y=y'7_2b.m输出:
y =
0.9812 0.0094
0.0054 0.4970
-0.0077 1.0193
0.3809 0.5839
1.0000 0.0000
0.0000 0.5000
0.0000 1.0000RBF网络逼近仿真


连续系统
课本p137 chap7_5.m

sinulink
function [sys,x0,str,ts]=s_function(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 3,
sys=mdlOutputs(t,x,u);
case {2, 4, 9 }
sys = [];
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 2;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys=simsizes(sizes);
x0=[];
str=[];
ts=[];
function sys=mdlOutputs(t,x,u)
persistent w w_1 w_2 b ci
alfa=0.05;
xite=0.5;
if t==0
b=1.5;
ci=[-1 -0.5 0 0.5 1;
-10 -5 0 5 10];
w=rands(5,1);
w_1=w;w_2=w_1;
end
ut=u(1);
yout=u(2);
xi=[ut yout]';
for j=1:1:5
h(j)=exp(-norm(xi-ci(:,j))^2/(2*b^2));
end
ymout=w'*h';
d_w=0*w;
for j=1:1:5 %Only weight value update
d_w(j)=xite*(yout-ymout)*h(j);
end
w=w_1+d_w+alfa*(w_1-w_2);
w_2=w_1;w_1=w;
sys(1)=ymout;离散系统
chap7_6.m(个人修改:对比不同高斯函数取值以及学习步长对逼近效果和过程的影响)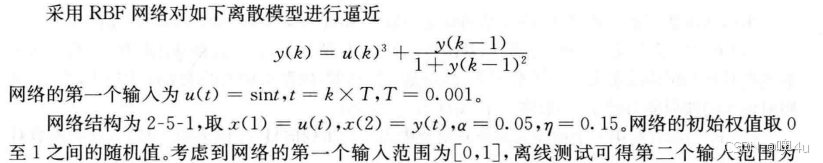

% RBF网络逼近分析与可视化
clear all;
close all;
% 定义参数组合
b_values = {0.3*ones(1,5), 3*ones(1,5), 30*ones(1,5)}; % 不同的高斯宽度 (行向量)
xite_values = [0.015, 0.15, 1.5]; % 不同的学习步长
num_b = length(b_values);
num_xite = length(xite_values);
% 创建图形窗口
figure;
set(gcf, 'Position', [100, 100, 1200, 800]);
% 迭代次数和时间步长
num_iter = 10000;
ts = 0.001;
time = (1:num_iter) * ts;
% 遍历所有参数组合
for i = 1:num_b
for j = 1:num_xite
% 参数设置
b = b_values{i};
xite = xite_values(j);
alfa = 0.05;
x = [0; 1]; %初始化输入
% RBF中心和权重初始化
c = [-1 -0.5 0 0.5 1;
-1 -0.5 0 0.5 1];
w = rand(5,1);
% 初始化权重更新变量
w_1 = w;
w_2 = w_1;
y_1 = 0;
% 预分配数组
u = zeros(1, num_iter);
y = zeros(1, num_iter);
ym = zeros(1, num_iter);
em = zeros(1, num_iter);
% 训练过程
for k = 1:num_iter
u(k) = sin(k * ts);
y(k) = u(k)^3 + y_1 / (1 + y_1^2); %目标输出
x(1) = u(k);
x(2) = y_1;
% 计算RBF激活值
% 确保 b 是行向量,(x - c) 是 2x5,平方后 sum((x - c).^2,1) 是 1x5
% Element-wise 除法
h = exp(-sum((x - c).^2, 1) ./ (2 * (b.^2))); %计算每个RBF单元的激活值
% 预测输出
ym(k) = w' * h';
% 误差
em(k) = y(k) - ym(k);
% 权重更新
d_w = xite * em(k) * h'; % h' 是 5x1
w = w_1 + d_w + alfa * (w_1 - w_2);
% 更新权重历史
y_1 = y(k);
w_2 = w_1;
w_1 = w;
end
% 绘图
subplot(num_b, num_xite*2, (i-1)*num_xite*2 + (j-1)*2 + 1);
plot(time, y, 'r', 'LineWidth', 1.5); hold on;
plot(time, ym, 'k:', 'LineWidth', 1.5);
xlabel('时间 (s)');
ylabel('输出');
title(sprintf('b = %.1f, xite = %.2f', b(1), xite));
legend('理想信号', '逼近信号');
grid on;
% 绘制误差
subplot(num_b, num_xite*2, (i-1)*num_xite*2 + (j-1)*2 + 2);
plot(time, em, 'k', 'LineWidth', 1.5);
xlabel('时间 (s)');
ylabel('误差');
title(sprintf('误差: b = %.1f, xite = %.2f', b(1), xite));
grid on;
end
end
% 添加总体标题
sgtitle('不同高斯宽度和学习步长下RBF网络的逼近效果及误差');

宽度和学习率的影响
不同高斯函数取值(宽度 b)对逼近效果的影响
-
较小的
b值:RBF单元对输入空间的局部特征响应更敏感,预测信号可能更接近目标信号,但误差曲线可能波动较大。- 高斯函数的宽度较窄,激活值更集中。
- 模型对局部特征的捕捉能力增强,但可能需要更多的RBF单元来覆盖输入空间。
- 可能导致过拟合,尤其在训练数据噪声较大时。
-
较大的
b值:RBF单元对全局特征响应更强,预测信号可能较为平滑,但可能无法准确捕捉目标信号的细微变化。- 高斯函数的宽度较宽,激活值更分散。
- 模型对全局特征的捕捉能力增强,通常需要较少的RBF单元。
- 可能导致欠拟合,无法充分捕捉数据的局部变化。
不同学习步长 (xite) 对逼近效果的影响
-
较大的学习步长:
- 权重更新幅度较大,收敛速度加快。
- 可能导致训练过程中的震荡或不稳定,难以精确收敛。
-
较小的学习步长:
- 权重更新幅度较小,收敛过程更加平稳。
- 训练速度较慢,可能需要更多的迭代次数才能达到收敛。
单神经元自适应控制


课本chap9_1.m

% 单神经自适应控制器
clear all; % 清除工作区中的所有变量
close all; % 关闭所有打开的图形窗口
% 初始化状态向量 x,包含三个元素,初始值为 0
x = [0, 0, 0]';
% 学习率,用于权重更新
xite = 0.40;
% 初始化权重 w1, w2, w3 的初始值
w1_1 = 0.10;
w2_1 = 0.10;
w3_1 = 0.10;
% 初始化误差的前两次值
e_1 = 0;
e_2 = 0;
% 初始化系统输出的前两次值
y_1 = 0;
y_2 = 0;
% 初始化控制输入的前两次值
u_1 = 0;
u_2 = 0;
% 采样时间间隔
ts = 0.001;
% 迭代循环,运行1000次
for k = 1:1:1000
time(k) = k * ts; % 当前时间点
% 生成参考信号 r(k),为一个方波信号,通过正弦函数的符号函数生成
r(k) = 0.5 * sign(sin(2 * 2 * pi * k * ts));
% 计算系统输出 y(k),基于前两次输出 y_1 和 y_2,以及前两次控制输入 u_1 和 u_2
y(k) = 0.368 * y_1 + 0.26 * y_2 + 0.1 * u_1 + 0.632 * u_2;
% 计算当前误差 e(k),为参考信号 r(k) 减去系统输出 y(k)
e(k) = r(k) - y(k);
% 通过监督Hebb学习算法调整权重值
% w1, w2, w3 分别对应不同的权重参数
w1(k) = w1_1 + xite * e(k) * u_1 * x(1); % 更新权重 w1
w2(k) = w2_1 + xite * e(k) * u_1 * x(2); % 更新权重 w2
w3(k) = w3_1 + xite * e(k) * u_1 * x(3); % 更新权重 w3
% 控制增益 K,用于控制律计算
K = 0.12;
% 更新状态向量 x,基于当前误差 e(k) 和前两次误差 e_1, e_2
x(1) = e(k) - e_1; % x(1) 为误差的一阶差分
x(2) = e(k); % x(2) 为当前误差
x(3) = e(k) - 2 * e_1 + e_2; % x(3) 为误差的二阶差分
% 构建权重向量 w,包含当前的三个权重值
w = [w1(k), w2(k), w3(k)];
% 计算当前控制输入 u(k) 基于前一个控制输入 u_1 和权重向量 w 及状态向量 x
u(k) = u_1 + K * w * x; % 控制律公式
% 更新误差的历史值,用于下次迭代
e_2 = e_1; % 第二次误差更新为第一次误差
e_1 = e(k); % 第一次误差更新为当前误差
% 更新控制输入的历史值,用于下次迭代
u_2 = u_1; % 第二次控制输入更新为第一次控制输入
u_1 = u(k); % 第一次控制输入更新为当前控制输入
% 更新系统输出的历史值,用于下次迭代
y_2 = y_1; % 第二次系统输出更新为第一次系统输出
y_1 = y(k); % 第一次系统输出更新为当前系统输出
% 更新权重的历史值,用于动量项的计算
w1_1 = w1(k); % w1 的历史值更新为当前 w1
w2_1 = w2(k); % w2 的历史值更新为当前 w2
w3_1 = w3(k); % w3 的历史值更新为当前 w3
end
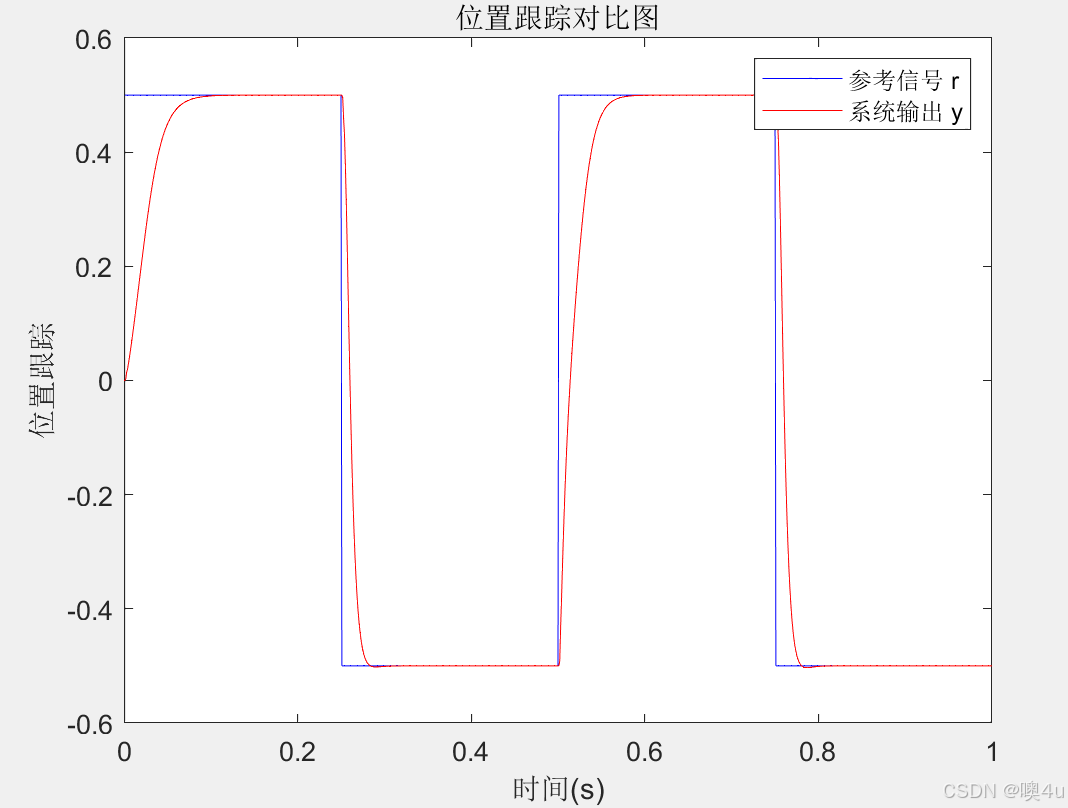
% 绘制参考信号 r 和系统输出 y 的位置跟踪图
figure(1);
plot(time, r, 'b', time, y, 'r'); % r 为蓝色线,y 为红色线
xlabel('时间(s)'); % x轴标签
ylabel('位置跟踪'); % y轴标签
legend('参考信号 r', '系统输出 y'); % 图例
title('位置跟踪对比图'); % 图形标题
% 绘制误差 e 随时间的变化图
figure(2);
plot(time, e, 'r'); % 误差以红色线表示
xlabel('时间(s)'); % x轴标签
ylabel('误差'); % y轴标签
title('误差随时间变化图'); % 图形标题
% 绘制权重 w1 随时间的变化图
figure(3);
plot(time, w1, 'r'); % w1 以红色线表示
xlabel('时间(s)'); % x轴标签
ylabel('w1'); % y轴标签
title('权重 w1 随时间变化图'); % 图形标题
% 绘制权重 w2 随时间的变化图
figure(4);
plot(time, w2, 'r'); % w2 以红色线表示
xlabel('时间(s)'); % x轴标签
ylabel('w2'); % y轴标签
title('权重 w2 随时间变化图'); % 图形标题
% 绘制权重 w3 随时间的变化图
figure(5);
plot(time, w3, 'r'); % w3 以红色线表示
xlabel('时间(s)'); % x轴标签
ylabel('w3'); % y轴标签
title('权重 w3 随时间变化图'); % 图形标题



RBF网络监督控制

 课本chap9_2.m
课本chap9_2.m
% RBF 监督控制
clear all; % 清除工作区中的所有变量
close all; % 关闭所有打开的图形窗口
% 设置采样时间间隔为0.001秒
ts = 0.001;
% 定义连续时间传递函数sys,分子为1000,分母为1s^2 + 50s + 2000
sys = tf(1000, [1, 50, 2000]);
% 将连续时间系统转换为离散时间系统,采样时间为ts,使用Z变换
dsys = c2d(sys, ts, 'z');
% 获取离散时间系统的分子和分母系数,'v'选项返回向量形式
[num, den] = tfdata(dsys, 'v');
% 初始化系统输出和控制输入的历史值
y_1 = 0; y_2 = 0; % 前两次系统输出
u_1 = 0; u_2 = 0; % 前两次控制输入
e_1 = 0; % 前一次误差
% 初始化输入变量
xi = 0;
x = [0, 0]'; % 状态向量,包含误差及其导数
% 定义RBF网络的参数
b = 0.5 * ones(4, 1); % 高斯核的宽度参数,四个RBF单元
c = [-2, -1, 1, 2]; % RBF核的中心位置
w = rand(4, 1); % 随机初始化权重向量
w_1 = w; w_2 = w_1; % 权重的历史值,用于动量项
% 定义学习率和动量参数
xite = 0.30; % 学习率
alfa = 0.05; % 动量项
% 定义PD控制器的增益参数
kp = 25; % 比例增益
kd = 0.3; % 微分增益
% 迭代循环,进行1000次仿真
for k = 1:1:1000
time(k) = k * ts; % 当前时间点
% 生成参考信号r(k)
S = 1; % 信号选择开关
if S == 1
r(k) = 0.5 * sign(sin(2 * 2 * pi * k * ts)); % 方波信号
elseif S == 2
r(k) = 0.5 * sin(3 * 2 * pi * k * ts); % 正弦波信号
end
% 计算系统输出y(k)基于离散系统的传递函数
y(k) = -den(2) * y_1 - den(3) * y_2 + num(2) * u_1 + num(3) * u_2;
% 计算当前误差e(k)
e(k) = r(k) - y(k);
% 将参考信号r(k)作为RBF网络的输入xi
xi = r(k);
% 计算每个RBF单元的激活值h(j)
for j = 1:1:4
h(j) = exp(-norm(xi - c(j))^2 / (2 * b(j)^2));
end
% 计算RBF网络的输出un(k)为权重w与激活值h的内积
un(k) = w' * h';
% 计算PD控制器的输出up(k)
up(k) = kp * x(1) + kd * x(2);
% 控制输出的选择
M = 2; % 控制模式选择开关
if M == 1 % 仅使用PD控制
u(k) = up(k);
elseif M == 2 % 总控制输出为PD控制加RBF网络输出
u(k) = up(k) + un(k);
end
% 控制输出饱和限制在[-10, 10]之间
if u(k) >= 10
u(k) = 10;
end
if u(k) <= -10
u(k) = -10;
end
% 在第400个时间步,施加额外的控制输入干扰
if k == 400
u(k) = u(k) + 6.0;
end
% 更新神经网络的权重,使用监督Hebb学习算法
d_w = -xite * (un(k) - u(k)) * h'; % 权重更新量
w = w_1 + d_w + alfa * (w_1 - w_2); % 包含动量项的权重更新
% 更新权重的历史值
w_2 = w_1;
w_1 = w;
% 更新控制输入的历史值
u_2 = u_1;
u_1 = u(k);
% 更新系统输出的历史值
y_2 = y_1;
y_1 = y(k);
% 更新状态向量x,用于PD控制器
x(1) = e(k); % 比例项
x(2) = (e(k) - e_1) / ts; % 微分项
e_1 = e(k); % 更新误差的历史值
end
% 绘制参考信号r和系统输出y的对比图
figure(1);
plot(time, r, 'r', time, y, 'b'); % r为红色线,y为蓝色线
xlabel('时间(s)'); ylabel('参考信号 r 和系统输出 y');
legend('参考信号 r', '系统输出 y'); % 添加图例
title('参考信号与系统输出的对比');
% 绘制RBF网络输出un、PD控制器输出up和总控制输出u随时间的变化图
figure(2);
subplot(3,1,1);
plot(time, un, 'b'); % RBF网络输出un为蓝色线
xlabel('时间(s)'); ylabel('RBF网络输出 un');
title('RBF网络输出随时间变化');
subplot(3,1,2);
plot(time, up, 'k'); % PD控制器输出up为黑色线
xlabel('时间(s)'); ylabel('PD控制器输出 up');
title('PD控制器输出随时间变化');
subplot(3,1,3);
plot(time, u, 'r'); % 总控制输出u为红色线
xlabel('时间(s)'); ylabel('总控制输出 u');
title('总控制输出随时间变化');


RBF直接模型参考自适应控制


课本chap9_4.m
% Model Reference Adaptive RBF Control 模型参考自适应径向基函数控制
clear all; % 清除所有变量
close all; % 关闭所有图形窗口
u_1=0; % 初始化控制输入u_1为0
y_1=0; % 初始化系统输出y_1为0
ym_1=0; % 初始化参考模型输出ym_1为0
x=[0,0,0]'; % 初始化状态向量x
c=[-3 -2 -1 1 2 3;
-3 -2 -1 1 2 3;
-3 -2 -1 1 2 3]; % 径向基函数的中心矩阵c
b=2*ones(6,1); % 径向基函数的宽度参数b
w=rands(6,1); % 初始化权重向量w为随机值
xite=0.35; % 学习率xite
alfa=0.05; % 衰减因子alfa
h=[0,0,0,0,0,0]'; % 初始化径向基函数输出h
w_1=w;w_2=w; % 初始化权重更新变量w_1和w_2
ts=0.001; % 采样时间ts
for k=1:1:3000 % 循环3000次
time(k)=k*ts; % 记录时间
r(k)=0.5*sin(2*pi*k*ts); % 生成参考信号r(k)
ym(k)=0.6*ym_1 + r(k); % 更新参考模型输出ym(k)
y(k)=(-0.1*y_1 + u_1)/(1 + y_1^2); % 非线性系统输出y(k)
for j=1:1:6 % 计算径向基函数的输出
h(j)=exp(-norm(x - c(:,j))^2/(2*b(j)^2)); % 计算第j个RBF的输出
end
u(k)=w' * h; % 计算控制输入u(k)
ec(k)=ym(k) - y(k); % 计算跟踪误差ec(k)
dyu(k)=sign((y(k) - y_1)/(u(k) - u_1)); % 计算dyu(k)的符号
d_w=0*w; % 初始化权重更新量d_w
for j=1:1:6 % 更新每个权重
d_w(j)=xite * ec(k) * h(j) * dyu(k); % 计算权重更新量
end
w=w_1 + d_w + alfa * (w_1 - w_2); % 更新权重向量w
u_1=u(k); % 更新上一时刻的控制输入
y_1=y(k); % 更新上一时刻的系统输出
ym_1=ym(k); % 更新上一时刻的参考模型输出
x(1)=r(k); % 更新状态向量x的第一个元素为参考信号
x(2)=ec(k); % 更新状态向量x的第二个元素为跟踪误差
x(3)=y(k); % 更新状态向量x的第三个元素为系统输出
w_2=w_1; % 更新w_2为w_1
w_1=w; % 更新w_1为当前权重w
end
figure(1); % 创建第一个图形窗口
plot(time, ym, 'r', time, y, 'b'); % 绘制参考模型输出和系统输出
xlabel('time(s)'); ylabel('ym, y'); % 设置坐标轴标签
figure(2); % 创建第二个图形窗口
plot(time, ym - y, 'r'); % 绘制跟踪误差
xlabel('time(s)'); ylabel('tracking error'); % 设置坐标轴标签


实验6 优化算法
遗传算法

 课本function_plot.m
课本function_plot.m
clear all;
close all;
x_min=-2.048;
x_max=2.048;
L=x_max-x_min;
N=101;
for i=1:1:N
for j=1:1:N
x1(i)=x_min+L/(N-1)*(i-1); %在x1轴上取100点
x2(j)=x_min+L/(N-1)*(j-1); %在x2轴上取100点
fx(i,j)=100*(x1(i)^2-x2(j))^2+(1-x1(i))^2;
end
end
figure(1);
surf(x1,x2,fx);
title('f(x)');
display('Maximum value of fx=');
disp(max(max(fx)));>> function_plot
Maximum value of fx=
3.9059e+03
课本chap10_1.m
%Generic Algorithm for function f(x1,x2) optimum
clear all;
close all;
%Parameters
Size=80;
G=100;
CodeL=10;
umax=2.048;
umin=-2.048;
E=round(rand(Size,2*CodeL)); %Initial Code
%Main Program
for k=1:1:G
time(k)=k;
for s=1:1:Size
m=E(s,:);
y1=0;y2=0;
%Uncoding
m1=m(1:1:CodeL);
for i=1:1:CodeL
y1=y1+m1(i)*2^(i-1);
end
x1=(umax-umin)*y1/1023+umin;
m2=m(CodeL+1:1:2*CodeL);
for i=1:1:CodeL
y2=y2+m2(i)*2^(i-1);
end
x2=(umax-umin)*y2/1023+umin;
F(s)=100*(x1^2-x2)^2+(1-x1)^2;
end
Ji=1./F;
%****** Step 1 : Evaluate BestJ ******
BestJ(k)=min(Ji);
fi=F; %Fitness Function
[Oderfi,Indexfi]=sort(fi); %Arranging fi small to bigger
Bestfi=Oderfi(Size); %Let Bestfi=max(fi)
BestS=E(Indexfi(Size),:); %Let BestS=E(m), m is the Indexfi belong to max(fi)
bfi(k)=Bestfi;
%****** Step 2 : Select and Reproduct Operation******
fi_sum=sum(fi);
fi_Size=(Oderfi/fi_sum)*Size;
fi_S=floor(fi_Size); %Selecting Bigger fi value
kk=1;
for i=1:1:Size
for j=1:1:fi_S(i) %Select and Reproduce
TempE(kk,:)=E(Indexfi(i),:);
kk=kk+1; %kk is used to reproduce
end
end
%************ Step 3 : Crossover Operation ************
pc=0.60;
n=ceil(20*rand);
for i=1:2:(Size-1)
temp=rand;
if pc>temp %Crossover Condition
for j=n:1:20
TempE(i,j)=E(i+1,j);
TempE(i+1,j)=E(i,j);
end
end
end
TempE(Size,:)=BestS;
E=TempE;
%************ Step 4: Mutation Operation **************
%pm=0.001;
%pm=0.001-[1:1:Size]*(0.001)/Size; %Bigger fi, smaller Pm
%pm=0.0; %No mutation
pm=0.1; %Big mutation
for i=1:1:Size
for j=1:1:2*CodeL
temp=rand;
if pm>temp %Mutation Condition
if TempE(i,j)==0
TempE(i,j)=1;
else
TempE(i,j)=0;
end
end
end
end
%Guarantee TempPop(30,:) is the code belong to the best individual(max(fi))
TempE(Size,:)=BestS;
E=TempE;
end
Max_Value=Bestfi
BestS
x1
x2
figure(1);
plot(time,BestJ);
xlabel('Times');ylabel('Best J');
figure(2);
plot(time,bfi);
xlabel('times');ylabel('Best F');>> chap10_1
Max_Value =
3.9059e+03
BestS =
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
x1 =
-2.0480
x2 =
-2.0480


粒子群算法

课本chap10_2.m
clear all;
close all;
%(1)初始化粒子群算法参数
min=-2.048;max=2.048;%粒子位置范围
Vmax=1;Vmin=-1;%粒子运动速度范围
c1=1.3;c2=1.7; %学习因子[0,4]
wmin=0.10;wmax=0.90;%惯性权重
G=100; % 最大迭代次数
Size=50; %初始化群体个体数目
for i=1:G
w(i)=wmax-((wmax-wmin)/G)*i; %随着优化进行,应降低自身权重
end
for i=1:Size
for j=1:2
x(i,j)=min+(max-min)*rand(1); %随机初始化位置
v(i,j)=Vmin +(Vmax-Vmin)*rand(1); %随机初始化速度
end
end
%(2)计算各个粒子的适应度,并初始化Pi、plocal和最优个体BestS
for i=1:Size
p(i)=chap10_2func(x(i,:));
y(i,:)=x(i,:);
if i==1
plocal(i,:)=chap10_2lbest(x(Size,:),x(i,:),x(i+1,:));
elseif i==Size
plocal(i,:)=chap10_2lbest(x(i-1,:),x(i,:),x(1,:));
else
plocal(i,:)=chap10_2lbest(x(i-1,:),x(i,:),x(i+1,:));
end
end
BestS=x(1,:);%初始化最优个体BestS
for i=2:Size
if chap10_2func(x(i,:))>chap10_2func(BestS)
BestS=x(i,:);
end
end
%(3)进入主循环
for kg=1:G
for i=1:Size
M=1;
if M==1
v(i,:)=w(kg)*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(plocal(i,:)-x(i,:));%局部寻优:加权,实现速度的更新
elseif M==2
v(i,:)=w(kg)*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(BestS-x(i,:)); %全局寻优:加权,实现速度的更新
end
for j=1:2 %检查速度是否越界
if v(i,j)<Vmin
v(i,j)=Vmin;
elseif x(i,j)>Vmax
v(i,j)=Vmax;
end
end
x(i,:)=x(i,:)+v(i,:)*1; %实现位置的更新
for j=1:2 %检查位置是否越界
if x(i,j)<min
x(i,j)=min;
elseif x(i,j)>max
x(i,j)=max;
end
end
%自适应变异,避免粒子群算法陷入局部最优
if rand>0.60
k=ceil(2*rand);
x(i,k)=min+(max-min)*rand(1);
end
%(4)判断和更新
if i==1
plocal(i,:)=chap10_2lbest(x(Size,:),x(i,:),x(i+1,:));
elseif i==Size
plocal(i,:)=chap10_2lbest(x(i-1,:),x(i,:),x(1,:));
else
plocal(i,:)=chap10_2lbest(x(i-1,:),x(i,:),x(i+1,:));
end
if chap10_2func(x(i,:))>p(i) %判断当此时的位置是否为最优的情况,当不满足时继续更新
p(i)=chap10_2func(x(i,:));
y(i,:)=x(i,:);
end
if p(i)>chap10_2func(BestS)
BestS=y(i,:);
end
end
Best_value(kg)=chap10_2func(BestS);
end
figure(1);
kg=1:G;
plot(kg,Best_value,'r','linewidth',2);
xlabel('generations');ylabel('Fitness function');
display('Best Sample=');disp(BestS);
display('Biggest value=');disp(Best_value(G));>> chap10_2
Best Sample=
-2.0480 -2.0480
Biggest value=
3.9059e+03
差分进化算法

























 7167
7167

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








