力扣hot100全部题解+代码（持续更新

————3/12————

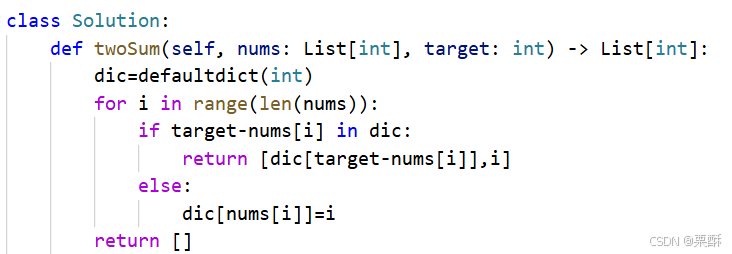
1.两数之和

哈希表：创建一个key为数组的值，value为下标的哈希表，遍历数组，在哈希表中寻找target-nums[i]是否存在，如果存在返回 target-nums[i]对应的下标值和当前遍历到的下标i，因为遍历到nums[i]时，其匹配的元素在前面一定已经遍历过了，可以保证顺序是正确的。

283.移动零

定义左右指针，只要右指针遇到非零的数就和左指针交换，左指针只有在交换的时候才右移，右指针一直右移，来保证left,right-1这个区间的数都是零

3.无重复字符的最长子串

双指针，滑动窗口：加入新元素后，如果有重复元素，就把全部重复元素移走，移完了之后更新最大长度

53.最大子数组和

dp:dp数组代表以当前数字结尾的最大子数组和，初始化数组为零，dp[0]为nums[0]，状态转移方程为dp[i] =max(dp[i-1],0)+nums[i]

73.矩阵置零

两次遍历，第一次遍历设置标志位，遍历数组中每一个元素，如果为零，则该列和改行的标志位都设置为0，重新设置一个zero_row=1标志位防止与第零列冲突。第二次遍历从第二行第二列的元素开始，如果该列或者该行标志位为0，则将该位置置零，然后如果第一列或者第一行标志位为零，将第一行或者第一列的元素置零

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        rows=len(matrix)
        cols=len(matrix[0])
        row_zero=1 #初始化为1，因为不一定第一排要为零
        for row in range(rows):
            for col in range(cols):
                if matrix[row][col]==0:
                    matrix[0][col]=0
                    if row>0:
                        matrix[row][0]=0
                    else:
                        row_zero=0
        
        for row in range(1,rows):
            for col in range(1,cols):
                if matrix[0][col]==0 or matrix[row][0]==0:
                    matrix[row][col]=0
        
        if matrix[0][0]==0:
            for row in range(rows):
                matrix[row][0]=0
        
        if row_zero==0:
            for col in range(cols):
                matrix[0][col]=0      

160.相交链表

设p,q分别为两个链表的头结点，只要pq不相遇，pq就一直往后走，走到末尾了就跳到对方链表的头结点上，如果他们会相遇，则他们走过的路程是相同的

94.二叉树的中序遍历

法一：迭代

用栈保存待访问的根节点。从根节点出发，一直往左下遍历，将每个左子树都放到栈里，循环条件是cur或者栈都不为空，（栈相当于cur的补给站）当cur为空了，就从栈中弹出元素（相当于访问中间节点）

class TreeNode:
    def __init__(self,val=None,left=None,right=None):
        self.val=val
        self.left=left
        self.right=right
class solution:
    def method(self,root,k):
        st=[]
        ans=[]
        cur=root
        while st or cur:
            while cur:
                st.append(cur)
                cur=cur.left
            cur=st.pop()
            ans.append(cur.val)
            cur=cur.right
        return ans[k-1]
    def toTree(self,nums):
        nums=[TreeNode(int(x)) if x!='null' else None for x in nums]
        root=nums[0]
        for i in range(len(nums)):
            left_idx,right_idx=2*i+1,2*i+2
            if left_idx<len(nums):
                nums[i].left=nums[left_idx]
            if right_idx<len(nums):
                nums[i].right=nums[right_idx]
        return root
if __name__=="__main__":
    import sys
    n,k=map(int,sys.stdin.readline().strip().split())
    nums=sys.stdin.readline().strip().split()
    root=solution().toTree(nums)
    ans=solution().method(root,k)
    print(ans)

法二：递归dfs

 200.岛屿数量

 bfs:层序遍历的作用是把所能遍历到的元素置零，因此循环遍历每一个非零元素，进行bfs搜索，每一次搜索都可以把一个岛屿划分出来

 22.括号生成

dfs:将生成过程看成一棵树，向左是加左括号，向右是加右括号，根据左右括号的数量判断可以走哪边，当左右括号都等于n时记录答案，当左括号小于n时可以添加左括号 ，当右括号小于n且右括号数量小于左括号时可以添加右括号，不用恢复现场，因为是直接在参数里面修改，相当于直接带到了下一层

35.搜索插入位置

闭区间二分查找

 20.有效的括号

栈：遇到左括号就加到栈里，遇到右括号就弹出栈顶元素开始配对，如果栈为空，或者不配对，返回false，访问完了所有括号，返回栈是否为空 

————3/13————

215.数组中第k个最大元素

构建小顶堆：heapify（），取数组的前k个元素，再对剩余元素进行处理，大于堆顶元素就pop处理，构建大顶堆的话就把数字取负数构建小顶堆

121.买卖股票的最佳时机

贪心：思路是每遍历一天价格，更新最大利润，更新最低价格。遍历每天价格，更新当前价格和最低价格之差，看和记录的最大利润谁大，再更新最低价格 

70.爬楼梯

dp:因为一次能跳两到三阶，所以站在当前的楼梯看，可能是从前一阶或者前两阶楼梯跳上来的，所以初始化dp为一和二的情况，注意数组大小至少都要预留两个位置

 62.不同路径

 dp:该位置路径等于左边+上边

136.只出现一次的数字

按位异或，相同的数字异或结果为0，0和数字异或为数字本身

 49.字母异位词

将每一个元素排序后作为字典的键，之后遍历到的元素如果键相同的话就加入到后续列表中去

 11.盛最多水的容器

双指针：短板效应，每次移动短的那一边，计算容量，更新最大容量 

438.找到字符串中所有字母异位词

滑动窗口：维护一个长度为len(p)的滑动窗口，用Counter容器统计窗口和p内的字母出现次数。枚举s的每个字母以及索引，枚举的过程相当于就是滑动窗口滑动的过程，滑动的时候比较counter内是否相等并动态更新left

239.滑动窗口

单调队列 ：pop->入队->popleft。如果当前元素比右边队口元素大，就把右边队口元素弹出来，将当前元素入队，如果超出k，就把左边队口元素弹出，然后左边队口就是最大元素。

56.合并区间

如果结果数组的右端大于当前数组左端，那结果数组的右端就再跟当前数组右端比一下看谁当新的右端，否则就把当前数组加到结果数组中去

54.螺旋矩阵

确定左上角的点和右下角的点，然后缩小遍历范围，在从右往左遍历时，要判断是否还能继续遍历 

206.反转链表

cur指向要改变指针的结点，所以要先记录下cur的下一个结点，然后pre和cur依次向后移，pre=cur，cur=nxt

234.回文链表

快慢指针找中间节点，翻转中间结点往后的链表，遍历两条链表，看是否相等

class Solution:
    def isPalindrome(self, head: Optional[ListNode]) -> bool:
        def find_mid(head):
            slow=fast=head
            while fast and fast.next:
                slow=slow.next
                fast=fast.next.next
            return slow
        
        def reverse(head):
            pre=None
            cur=head
            while cur:
                nxt=cur.next
                cur.next=pre
                pre=cur
                cur=nxt
            return pre
        
        mid=find_mid(head)
        new_mid=reverse(mid)
        while new_mid:
            if head.val!=new_mid.val:
                return False
            head=head.next
            new_mid=new_mid.next
        return True

————3/14—————

104.二叉树的最大深度

法一：递归（自下而上

当前层的最大深度等于左子树和右子树最大深度加一 

法二：自上而下

自上而下统计每一层经过了多少个节点，更新最大节点数，再递归下一层

226.翻转二叉树 

将根节点的左子树换成右子树，右子树换成左子树，再将根节点返回给上一层

 100.相同的树

如果两个根节点有一个为空，那么只有两个都为空时才返回True。如果都不为空，那么这一层要递归的结果就是根节点的值是否相等以及两棵树的左右子树是否相等 

 101.对称二叉树

根节点已经对称，分成左子树和右子树，看左右子树是否对称，和100题相同的树代码差不多，将左右子树作为参数传入判断对称的函数即可。

994.腐烂的橘子

bfs:不同于岛屿问题，现在是多个橘子同时开始腐烂，因此一开始就要把所有初始是腐烂的橘子全部加入到队列里面去，然后遍历队列里所有的腐烂橘子进行第一轮传播，然后又从所有新加进去的橘子里开始传播

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        m,n=len(grid),len(grid[0])
        fresh=0
        cnt=0
        q=collections.deque()
        directions=([1,0],[-1,0],[0,1],[0,-1])
        for i in range(m):
            for j in range(n):
                if grid[i][j]==1:
                    fresh+=1
                if grid[i][j]==2:
                    q.append([i,j])
        while q and fresh>0: #循环条件
            for i in range(len(q)):
                x,y=q.popleft() #弹出左边元素，popleft()
                for dx,dy in directions:
                    nx=x+dx
                    ny=y+dy
                    if 0<=nx<m and 0<=ny<n and grid[nx][ny]==1:
                        q.append([nx,ny])
                        grid[nx][ny]=2
                        fresh-=1
            cnt+=1
        if fresh>0:
            return -1
        else:
            return cnt
        

 79.单词搜索

dfs，回溯:从任意位置开始搜索第k个字符， 并递归访问四周字符，再恢复现场，返回的是下一层是否能找到的结果

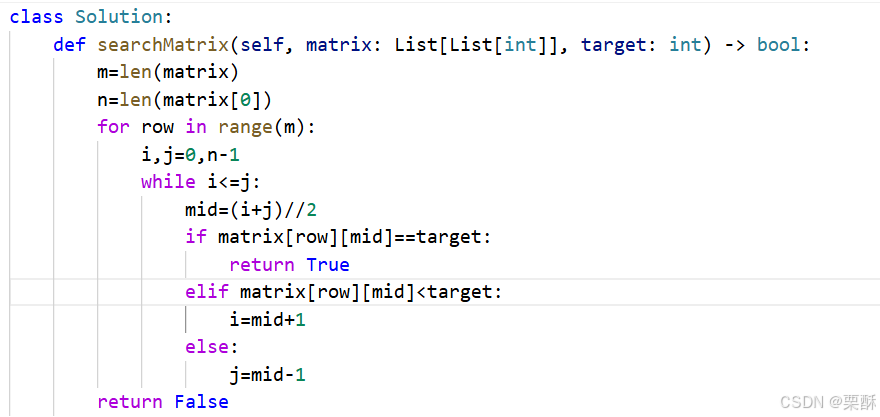
74.搜索二维矩阵

 二分查找：在一个二维矩阵中搜索某一个目标值，二维矩阵有序，可以用二分查找的方式。把二维矩阵拉成一维矩阵，一维矩阵的坐标mid对应到二维矩阵中去，横坐标等于mid//列数，纵坐标等于mid%列数。

155.最小栈

栈中存一个元组，第一个是当前值，第二个是当前栈的最小值，初始化栈时，在队尾放一个哨兵，最小值存为inf，可以避免判空的情况

 347.前k个高频元素

 统计每个数字的频率，以频率为标准存进小顶堆中，小顶堆：先统计每个元素出现的频率，用字典保存，然后使用小顶堆存储键值对，只要堆的大小还小于k，就往堆里加元素，堆的大小等于k后，只要待加入的元素大于堆顶元素，弹出堆顶元素，加入堆，最后输出堆里的元素

简化版

原版

 ————3/15—————

 55.跳跃游戏

枚举每一个位置和跳的距离，如果当前最大能跳的距离小于了i，说明跳不到，否则就更新当前i所能跳到的最大距离是否比之前的最大距离大

45.跳跃游戏Ⅱ

造桥：遍历每个走过的i，记录最大能造的桥的长度，如果走到桥的尽头，就造桥，不用遍历到最后一个元素，因为终点不用造桥。

64.最小路径和

 分四种情况，第一个点，第一排，第一列，和其他的点，第一排第一列只能从一个方向过来，因此路径和是可以求得，第一个点直接用原来的值，中间的点从两个方向选一个最小值加上自身的值

 

 118.杨辉三角

 把数组初始化为1，然后从第三行第二列开始进行计算

 169.多数元素

用哈希表记录元素出现次数，如果其出现次数大于数组长度的一半，则返回

128.最长连续序列

先去重，加到集合里，判断num-1是否在集合中，不在就重新计算长度，计算从当前位置开始一共有多长，更新最大长度 

 15.三数之和

将数组排序，循环遍历数组元素，每一次确定左右指针， 根据与0的大小关系移动指针，要去除重复情况，i和left

 189.轮转数组

全部翻转，前k个元素翻转，后面剩余元素翻转 

 ————3/16————

76.最小覆盖字串

ans_left,ans_right记录最小覆盖子串的左右边界，移动右指针，只要满足条件，就循环左移左指针，并更新左右边界

 48.旋转图像

保存左上角元素，顺时针替换，for循环结束，代表一圈的元素旋转完毕，改变left ,right的值 

 141.环形链表

快慢指针

142.环形链表Ⅱ

题解： 

快慢指针相遇，快指针到头结点，都一步一步地走，直到相遇 

 21.合并两个有序链表

递归：比较两个链表头结点的值，取较小的当新的链表当头结点，然后递归合并剩下部分，返回头结点

207.课程表

先修课和课程以哈希表的形式存储，每个课程有多少先修课以indeg数组表示，度为零说明没有先修课了，加入队列 

34.在排序数组中查找元素的第一个和最后一个位置

二分查找找到目标后，兵分两路行动

394.字符串解码

栈：遇到数字计算数字，遇到左括号将res和num加入栈，遇到右括号弹出计算现在的res，是上一次的res加上数字乘以res，遇到字母直接加到res上

131.分割回文串

4.寻找两个正序数组的中位数

寻找中位数，转换成合并两个数组寻找第k大的数，中位数就是寻找（中位数下标+1）大的数。定义函数找合并数组里第k大的元素，转换为两半， k//2和k-k//2，如果最后一个元素小于另一半的最后一个元素，则将该组元素全部砍掉，继续寻找砍掉后的第k-(被砍掉的元素)大的数。注意防止数组越界，要比较k和本身数组大小，取最小值

————3/3—————

  739.每日温度

 栈：循环遍历数组中的元素，如果该元素比栈顶元素大，弹出栈顶元素，并更新其更高温度出现在几天后，把栈里所有比该元素小的值都弹出后，再把该元素加入到栈里

295.数据流的中位数 

利用栈：建立大顶堆b和小顶堆a，如果两堆大小不一样，则将元素加入到大顶堆b中，但是要先加入到小顶堆中，然后把小顶堆的最小元素加入到大顶堆中，如果两堆大小相等，则将元素加入到小顶堆中，但是要先将元素加入到大顶堆b中再将大顶堆的最大元素加入到小顶堆中。最后如果两堆大小不相等则返回小顶堆的最小元素，否则返回两堆顶元素的一半。 注意最后是差除以二，因为大顶堆中的元素都是负数

45.跳跃游戏Ⅱ 

贪心：i只到最后一个位置之前。维护每次跳跃能到达的区间，用end来表示区间边界，maxPos来表示在本次区间中能到达的最远距离，只要达到了区间的末尾，就重新起跳，把区间末尾设置为本次能到达的最远位置。

 198.打家劫舍

动态规划：偷到最后一个房间能偷到的最多金额，等于不偷最后一间房间的情况+偷最后一间房间的情况，不偷最后一间房间，那就是偷前i-1间房间的最大金额，偷最后一间房间，那就是前i-2间的最大金额加上最后一间的金额。一共开辟n+1个空间，因为还有偷0间房间的情况

 322.零钱兑换

个数与顺序无关，所以先遍历硬币或者背包都可以，先遍历硬币，容量从硬币的面额开始，该容量的最多硬币数量等于不装该硬币的硬币个数加一和现有最大个数的最小值

279.完全平方数

和零钱兑换思路一样，不同的点在于物品的取值范围，从1到n**0.5，j是从num*num到n

5.最长回文子串

中心扩散法：循环遍历每个元素，如果是奇数，从该元素往两边扩散，更新最长回文子串长度并记录起始位置，如果是偶数，以当前元素和下一个元素为中心往两边扩散 

75.颜色分类

 三指针法：l，r和i，i指向还没有排好序的元素，在l<=r的情况下，如果i指向的元素为2，则交换i和r指针指向的元素，左移右指针，如果i指向的元素为0，则交换i和l指向的元素，同时移动l和i指针，如果i指向的元素为1，则不交换，只移动i指针

————3/4——————

 42.接雨水

法一：单调栈

若栈口元素小于等于栈顶元素，入栈。若栈口元素大于栈顶元素，循环以下过程直到栈口元素小于栈顶元素：弹出栈顶元素记录下标为mid，选取栈口元素和新的栈顶元素的最小值（较小高度）减去中间柱子的高度，乘以栈顶元素到新的栈顶元素的宽度，就是雨水面积

法二：双指针

定义左右指针分别记录左边的最大高度和右边的最大高度，如果左边大于右边，右移左指针，取新的左指针高度和maxL的最大值，再加上maxL-height[left]的值，右指针同理

238.除自身以外数组的乘积

前缀积*后缀积：从左往右遍历，得到每个元素的前缀积，再从右往左遍历，用前缀积*后缀积

2. 两数相加

 从左往后相加，用ListNode创建相加后的新结点，head指向这个结点用于最后返回结果，相加后的v%10等于该位结果，v//10等于下一位的进位

240.搜索二维矩阵

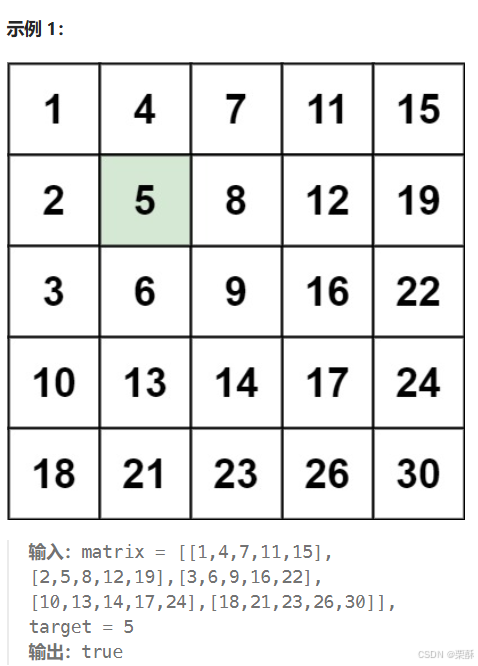
法一：转换成二叉搜索树 

从左下角开始，比目标元素大就向上移动，比目标元素小就向右移动 

二分查找：对每一层都使用二分查找，遍历row

 19.删除链表的倒数第N个结点

 快慢指针：定义一个虚拟结点指向头节点，快指针指向head，慢指针指向虚拟结点，先让快指针移动n步，再让快慢指针同时移动直到快指针指向空结点，此时慢指针指向要删除元素的上一个结点，可以直接删除，最后返回的是虚拟结点的下一个结点

24.两两交换链表中的节点

递归：定义一个tmp结点指向要交换的第二个结点，第一个结点指向下一组交换后的第一个结点，然后第二个结点指向第一个结点，然后返回tmp

class ListNode:
    def __init__(self,val=None,next=None):
        self.val=val
        self.next=next
class solution:
    def method(self,head):
        if not head or not head.next:return head #没有或者只有一个节点的情况
        tmp=head.next
        head.next=self.method(tmp.next)
        tmp.next=head
        return tmp
    def toList(self,nums):
        if not nums:return None #如果是空数组
        head=ListNode(nums[0])
        cur=head
        for num in nums[1:]:
            cur.next=ListNode(num)
            cur=cur.next
        return head
    def printList(self,head):
        cur=head
        ans=[]
        while cur:
            ans.append(cur.val)
            cur=cur.next
        print(" ".join(map(str,ans)))
if __name__=="__main__":
    import sys
    n=int(sys.stdin.readline().strip())
    nums=list(map(int,sys.stdin.readline().strip().split()))
    head=solution().toList(nums)
    newhead=solution().method(head)
    solution().printList(newhead)
        

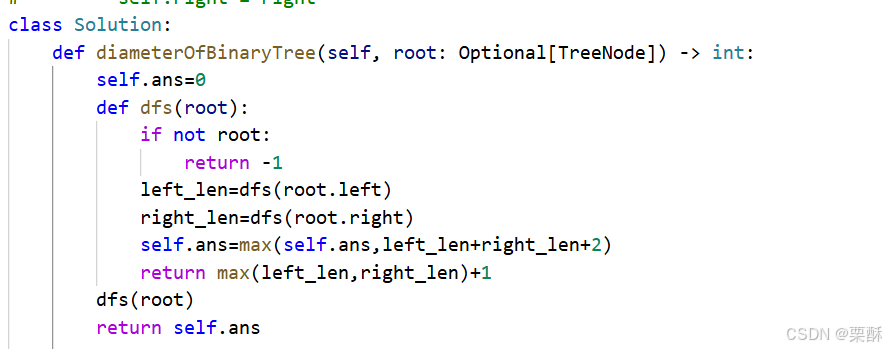
 543.二叉树的直径

dfs搜索：计算直径，就是左链的长度加右链的长度再加二，递归的去计算左右链的长度，也就是每次递归都返回左右链长度的最大值加上一 。也就是在计算深度的同时计算直径，边界条件为返回-1

102.二叉树的层序遍历

bfs搜索： 循环遍历这一层的元素加入到临时数组中，将这一层元素的子孩子加入到队列中，这一层遍历结束后加入到结果数组中

108.将有序数组转换为二叉搜索树

————3/7——————

 98.验证二叉搜索树

法一：最大值最小值 

当前节点的值是左子树的上界，右子树的下界，构造一个函数传入root和最大值最小值，递归的判断左子树和右子树是否满足条件

法二：中序遍历

如果中序遍历是递增顺序，则是二叉搜索树，边遍历边判断当前值是否大于上一个节点的值

 230.二叉搜索树中第k小的元素

对该二叉搜索树进行中序遍历保存到数组中，然后返回第k-1个元素 

也可以在访问到第k个元素的时候提前结束访问，使用一个全局变量来保存k和res的值

199.二叉树的右视图 

层序遍历，先判断是否有根节点，在有根节点的情况下，将每一层的最后一个元素加入到队列中，不能直接加结点，因为结点是不可迭代的类型，要以列表的形式加入，在过程中队列的长度是动态变换的，所以要用一个变量去记录队列的长度，

208.实现Trie（前缀树）

一个单词里的每一个字母都看作是一个字典的键，不同单词的相同字母共用这些键，不同字母就分支出去生成新的键。通过node=node[s]来嵌套遍历下一个字母

import collections
class Trie:
    def __init__(self):
        self.dic=collections.defaultdict(list)
    def insert(self,word):
        dic=self.dic
        for c in word:
            if c not in dic.keys():
                dic[c]=collections.defaultdict(list)
            dic=dic[c]
        dic['#']='#'
    def search(self,word):
        dic=self.dic
        for c in word:
            if c not in dic.keys():
                return False
            dic=dic[c]
        return '#' in dic.keys()
    def startsWith(self,prefix):
        dic=self.dic
        for c in prefix:
            if c not in dic.keys():
                return False
            dic=dic[c]
        return True
if __name__=="__main__":
    import sys
    n=int(sys.stdin.readline().strip())
    Trie=Trie() #只实例化一次
    for _ in range(n):
        do=sys.stdin.readline().strip().split()
        if do[0]=="insert":
            Trie.insert(do[1])
        elif do[0]=="search":
            print('true' if Trie.search(do[1]) else 'false')
        else:
            print('true' if Trie.startsWith(do[1]) else 'false')
        

class Trie:

    def __init__(self):
        self.child=defaultdict(dict)

    def insert(self, word: str) -> None:
        node=self.child
        for s in word:
            if s not in node.keys():
                node[s]=defaultdict(dict)
            node=node[s]
        node["#"]="#"
        
    def search(self, word: str) -> bool:
        node=self.child
        for s in word:
            if s in node.keys():
                node=node[s]
            else:
                return False
        return "#" in node.keys() 
        
    def startsWith(self, prefix: str) -> bool:
        node=self.child
        for s in prefix:
            if s in node.keys():
                node=node[s]
            else:
                return False
        return True

 51.N皇后

递归+回溯：目的是通过算法最后能得到每行的皇后最后在哪一列，用col数组表示，在算法中需要三个布尔类型的数组，分别表示一个元素的该列，左上，右上三个位置是否已经有皇后了，左斜线上的元素纵坐标横坐标之差相等，右斜线位置横纵坐标之和相等，一共有2n-1个元素，如果没有的话，将皇后放置在这个位置，并递归下一行并回溯，如果已经到了最后一行，则说明已经得到了col数组，根据col数组可以将皇后打印出来

33.搜索旋转排序数组

二分查找：数组旋转之后有序区间被一分为二，一段的最小值大于另一段的最大值，因此我们在二分查找的过程中，通过判断mid落在哪一个区间去缩小左右指针位置

 153.寻找旋转排序数组中的最小值

二分查找：旋转后同样把数组分成两个递增区间，最小值一定在第二个区间里面，所以最后要注意right=mid，比如【3，1，2】这个测试用例

763.划分字母区间

贪心：遍历字符串，通过枚举的方式统计每个字母出现的最远下标位置，重新遍历字符串，更新right的最大值，当i==right的时候说明这个区间包含了所有该出现的字母，将区间长度加入结果数组，更新left的位置

139.单词拆分

动态规划：f[i]表示前i个字符是否可以由字典里的单词表示。i循环遍历字符串，j从i+1的位置开始遍历，如果f[i]的状态为True并且[i,j-1]的位置在字典中，说明可以拼接，将其状态设为True 

————3/8—————

 300.最长递增子序列

动态规划：遍历数组元素，如果该元素比之前某个元素大，那么以该元素结尾的递增子序列等于之前以某个元素结尾的递增子序列加一，在过程中记录递增子序列的最大值 

1143.最长公共子序列

 多维动态规划：建立一个二维表，循环遍历两个字符串，如果当前两2个字符串的字符相等，那么最长公共子序列等于dp[i-1][j-1]+1，如果不相等，就取两种情况的最大值：包含第一个字符串的结尾或者包含第二个字符串的结尾，注意dp数组的长度比字符串多一个空间，当字符串遍历到了第i个位置，dp数组应该是i+1个位置

 31.下一个排列

倒序遍历，找到第一个正序的位置，如果这个位置为0，则将整个数组反转即可，如果不为0，那么从后往前找到第一个大于该位置的数，将其交换位置，然后反转该位置之后的数组

206.反转链表

定义pre为None，cur为head，cur指向待反转的结点，修改内部结点方向，cur指向pre，然后移动pre和cur指针，知道cur为空，返回pre结点

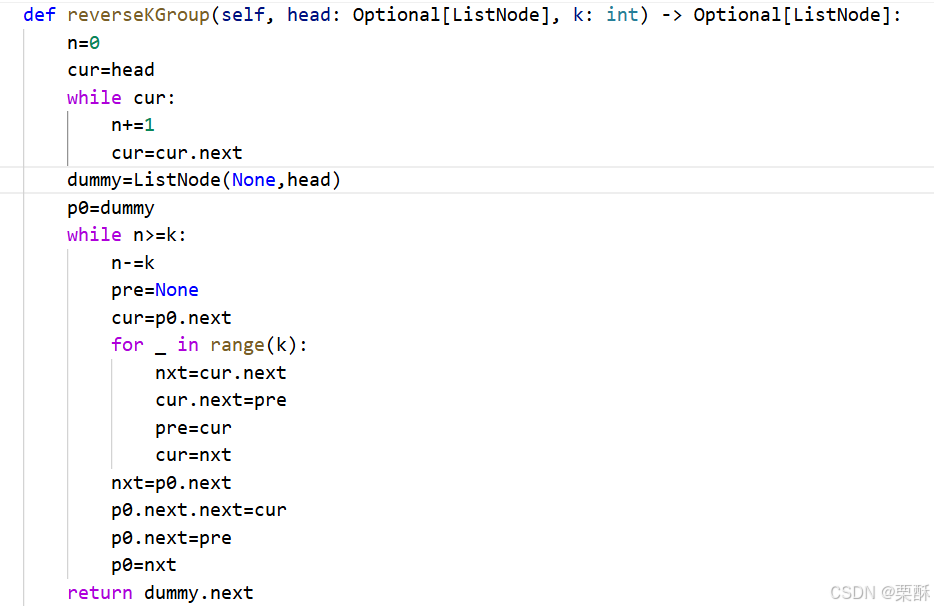
 25.k个一组翻转链表

遍历链表获得链表长度，只要链表长度大于等于k就做翻转，定义一个虚拟结点指向头节点，p0指向虚拟结点，（p0一直指向待翻转链表头节点的上一个结点），pre结点指向None，cur指向p0的next结点。保存cur的next结点，cur指向pre，pre和cur各向后移一个结点，循环k次（到这里是k个元素内部完成了指针翻转，接下来需要将外部指针翻转），保存p0的next结点，p0的next的next结点指向cur，p0的next指向pre，p0指向之前保存的p0的next结点。

class ListNode:
    def __init__(self,val=None,next=None):
        self.val=val
        self.next=next
class solution:
    def method(self,head,k):
        cur=head
        cnt=0
        while cur:
            cnt+=1
            cur=cur.next
        dummy=ListNode(None,head)
        p=dummy
        while cnt>=k:
            cnt-=k
            pre=None
            cur=p.next
            for _ in range(k):
                nxt=cur.next
                cur.next=pre
                pre=cur
                cur=nxt
            tmp=p.next
            p.next.next=cur
            p.next=pre
            p=tmp
        return dummy.next


    def toList(self,nums):
        head=ListNode(nums[0])
        cur=head
        for num in nums[1:]:
            cur.next=ListNode(num)
            cur=cur.next
        return head
    def printList(self,head):
        cur=head
        ans=[]
        while cur:
            ans.append(cur.val)
            cur=cur.next
        print(" ".join(map(str,ans)))

if __name__=="__main__":
    import sys
    nums=list(map(int,sys.stdin.readline().strip().split()))
    k=int(sys.stdin.readline().strip())
    head=solution().toList(nums)
    newhead=solution().method(head,k)
    solution().printList(newhead)

114.二叉树展开为链表

cur初始化为root，cur一直移动到其右子树的节点上，如果cur存在左子树，就把左子树拼接到cur和cur的右子树中间，拼接方法：找到cur左子树最下边的右子树，将右子树拼接到cur的右子树上，cur的右子树指向cur的左子树，将左子树置空

class TreeNode:
    def __init__(self,val=None,left=None,right=None):
        self.val=val
        self.left=left
        self.right=right
class solution:
    def method(self,root):
        cur=root
        while cur:
            if cur.left:
                p=cur.left
                while p.right: ##不是while p
                    p=p.right
                p.right=cur.right
                cur.right=cur.left
                cur.left=None
            cur=cur.right
        return root
    def toTree(self,nums):
        nums=[TreeNode(int(x)) if x!='null' else None for x in nums]
        root=nums[0]
        for i in range(len(nums)): ##不是从1开始
            if nums[i]:
                l_idx,r_idx=2*i+1,2*i+2
                if l_idx<len(nums):
                    nums[i].left=nums[l_idx]
                if r_idx<len(nums):
                    nums[i].right=nums[r_idx]
        return root
    def layer_print(self,root):
        import collections
        ans=[]
        q=collections.deque([root])
        while q:
            u=q.popleft()
            if u:
                ans.append(u.val)
                q.append(u.left)
                q.append(u.right) 
            else:
                ans.append("null")
        while ans and ans[-1]=="null": #弹出多余的null
            ans.pop()
        print(" ".join(map(str,ans)))
if __name__=="__main__":
    import sys
    nums=sys.stdin.readline().strip().split()
    root=solution().toTree(nums)
    new_root=solution().method(root)
    solution().layer_print(new_root)

46.全排列

递归+回溯：idx表示一共排好了多少个元素，如果idx等于数组长度，则把当前排列加入到res数组中，注意要使用排列数组的浅拷贝，不然后续修改排列数组的话res里面数组也会被修改。如果idx不等于数组长度，则遍历数组，找到没有被使用过的元素加入到排列数组中去，设置为已被使用并进入下一个递归函数中去，并进行回退

一：个数

二：下标 

20.有效的括号 

栈：利用一个字典来存储右括号对应的左括号，遍历s中每一个括号，如果不在字典中就说明是左括号，加入到栈中，如果是右括号，那么栈中为空或者栈顶元素和右括号对应的左括号不相等的话返回False，最后返回栈是否为空

————3/9—————

 152.乘积最大的子数组

动态规划：以第i个位置结尾的最大子数组乘积，是在以第i-1个位置结尾的子数组乘积的最大值*第i个元素的值，第i-1个位置结尾的子数组乘积的最小值*第i个元素的值，和第i个元素的值中取最大值，注意这里要使用一个临时变量记录原始的最大最小值，使用一个全局最大值记录遍历过程中的最大子数组的乘积，还要从第二个元素开始遍历。

416.分割等和子集

01背包问题：背包目标是装满集合所有元素和的一半，用01背包的思路解决

72.编辑距离

        

多维动态规划：两个字符串的最后一个字符相同，等于前i-1，j-1个字符串的修改次数，不相同，就从下面三种情况选最小值：删除第一个字符串的最后一个个字符，则为dp[i-1][j]+1，删除第二个字符串的最后一个字符：dp[i][j-1]+1，替换两个字符串的最后一个字符：dp[i-1][j-1]+1，删除和插入是可逆的逻辑，只需要考虑一种情况即可。

287.寻找重复数

快慢指针：因为空间复杂度为O（1），所以用指针，把数组看成链表，如果有重复元素，则一定有环，入口元素为重复元素，先通过快慢指针相遇，然后把快指针退回到初始位置，初始位置和相遇位置到入口元素的距离相等，快慢指针都移动一步直到相遇，返回慢指针元素

78.子集

回溯：树中的每个结点都是结果集中的答案，与全排列的区别在于数组是从idx开始遍历，将i+1作为下一层递归的idx，全排列还要看每个元素是否被使用过。

————3/10—————

 138.随机链表的复制

哈希表：利用哈希表来存储旧结点和新节点的对应关系，注意要用get方法来正确处理空值。遍历两次链表，第一次复制结点，第二次建立指针关系

148.排序链表

归并排序：分为两个部分，分割和合并。使用快慢指针的方法找到中间结点并一分为二，分别对两个链表排序，并合并 。合并时需要建立一个虚拟指针和一个尾指针，尾指针始终指向结果链表的末尾，两个链表中较小元素连接到尾指针后面，最终把剩余元素全部接到尾指针的部分

class Solution:
    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        def merge(left,right):
            dummy=ListNode(None)
            tail=dummy
            while left and right:
                if left.val<right.val:
                    tail.next=left
                    left=left.next
                else:
                    tail.next=right
                    right=right.next
                tail=tail.next
            if left:
                tail.next=left
            if right:
                tail.next=right
            return dummy.next
        #or 不是 and,否则递归不会终止
        if not head or not head.next:
            return head
        slow,fast=head,head.next
        while fast and fast.next:
            slow=slow.next
            fast=fast.next.next
        second=slow.next
        slow.next=None
        first=head
        first=self.sortList(first)
        second=self.sortList(second)
        return merge(first,second)

105.从前序遍历和中序遍历序列构造二叉树

前序遍历中的第一个结点为根节点，在中序遍历中找到根节点的下标，写出左右子树的前序和中序遍历序列，从而递归的构造左右子树

class TreeNode:
    def __init__(self,val=None,left=None,right=None):
        self.val=val
        self.left=left
        self.right=right

class solution:
    def method(self,preorder,inorder):
        if not preorder or not inorder:return None #排除特殊情况
        root_val=preorder[0]
        root=TreeNode(root_val)
        root_idx=-1
        for i in range(len(inorder)):
            if inorder[i]==root_val:
                root_idx=i
                break
        left_preorder=preorder[1:1+root_idx]
        right_preorder=preorder[1+root_idx:]
        left_inorder=inorder[:root_idx]
        right_inorder=inorder[root_idx+1:]

        left_root=self.method(left_preorder,left_inorder) #有递归的一定要排除特殊情况
        right_root=self.method(right_preorder,right_inorder)
        root.left=left_root
        root.right=right_root
        return root
    def layer_print(self,root):
        if not root: return []
        import collections
        q=collections.deque([root])
        ans=[]
        while q:
            u=q.popleft()
            if u:
                ans.append(u.val)
                q.append(u.left)
                q.append(u.right)
            else:
                ans.append("null")
        while ans and ans[-1]=="null":
            ans.pop()
        return ans
if __name__=="__main__":
    import sys
    n,m=map(int,sys.stdin.readline().strip().split())
    preorder=list(map(int,sys.stdin.readline().strip().split()))
    inorder=list(map(int,sys.stdin.readline().strip().split()))
    root=solution().method(preorder,inorder)
    ans=solution().layer_print(root)
    print(" ".join(map(str,ans)))

437.路径总和Ⅲ

法一：前缀和+哈希表

哈希表中存储每个节点的前缀路径和，注意要加入0对应的值，使用dfs遍历树的每个节点，在遍历过程中，ans直接加上当前节点的路径和减去targetSum的键对应的值，因为这里定义的是具有默认值的字典，然后存储当前路径和，再递归遍历左子树和右子树，恢复现场继续遍历当前节点父节点的右子树。

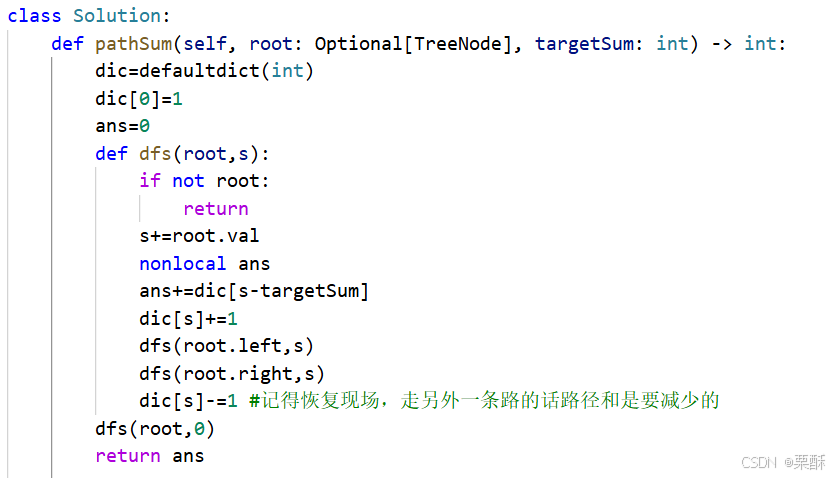
法二：dfs

560.和为k的子数组（和437题一样）

前缀和加哈希表：哈希表中存储每个元素的前缀和，在遍历数组时，计算每个元素的前缀和，在哈希表中查询当前前缀和减去k是否在哈希表中，如果在，说明存在和为k的子数组，然后再把当前前缀和存储到哈希表中

 17.电话号码的字母组合

回溯：dfs函数的参数值是遍历到digits的第几个数字，也就是第几个按键，如果递归到了第i个按键，就遍历该按键所包含的所有字母，再递归遍历下一个按键，再恢复现场。

 41.缺失的第一个正数

 原地哈希：很神奇的思路...遍历数组中元素，如果这个数在1到n（数组长度）之间，并且不和待交换位置元素相等，则交换该位置元素和该数字减一对应的下标的元素，再遍历一次数组，如果该位置的元素值不等于下标值加一，则返回下标值加一，如果都满足条件，则返回n+1，注意不能.nums[i], nums[nums[i] - 1] = nums[nums[i] - 1], nums[i]，会改变nums[i]的值

39.组合总和

回溯：组合问题，需要有st避免出现重复的情况，可以重复取元素，因此在进入下一层递归时，仍然是从第i个位置开始取元素，st为i，在最后收获结果的时候，要将path的拷贝加入到ans中

————3/11—————

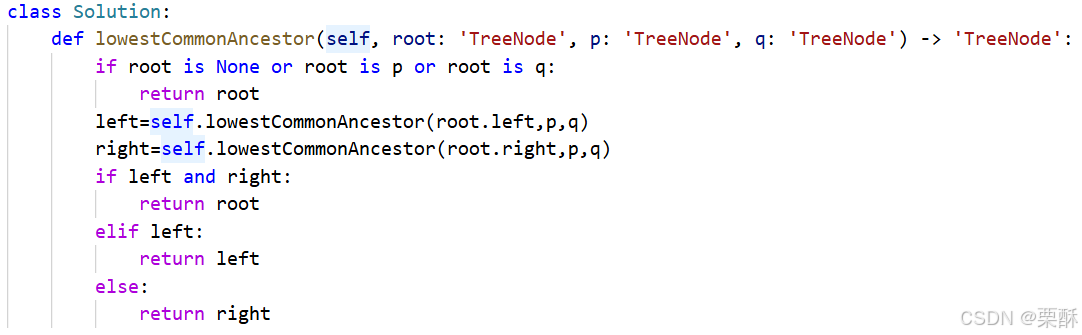
 236.二叉树的最近公共祖先

 在遍历时只要找到p或者q中的其中一个都可以停止遍历了，因为pq本身也可以作为公共祖先，先判断根节点是否为p或者q或者是空结点，如果是的话直接返回根节点，如果不是则递归遍历左右子树，如果左右子树都找到了，则返回根节点，如果只在左子树找到了，则返回左子树找到的那个节点，反之不管右子树找没找到都返回右子树。

146.LRU缓存

双向链表+哈希表：使用一个哈希表存储key和结点的映射，get相当于抽出一本书放到最顶层并返回该书的值，put，如果有这本书，就抽出这本书放在最顶层并修改它的值，如果没有这本书，就创建对应的哈希映射并把这本书放到最顶层，如果超出缓存容量，则删除最后一个结点的哈希映射以及这个结点 。提取一个getnode方法把这本书抽出来放到最顶层。

class ListNode:
    def __init__(self, key=0,val=0,pre=None,next=None):
        self.key=key
        self.val=val
        self.pre=pre
        self.next=next

class LRUCache:

    def __init__(self, capacity: int):
        self.capacity=capacity
        self.key_to_node=dict()
        self.dummy=ListNode()
        self.dummy.pre=self.dummy
        self.dummy.next=self.dummy
    
    def getnode(self,key)->ListNode:
        if key not in self.key_to_node:
            return None
        node=self.key_to_node[key]
        self.remove(node)
        self.put_top(node)
        return node

    def get(self, key: int) -> int:
        node=self.getnode(key)
        return node.val if node else -1

    def put(self, key: int, value: int) -> None:
        node=self.getnode(key)
        if node:
            node.val=value
            return
        else:
            self.key_to_node[key]=node=ListNode(key,value,None,None)
            self.put_top(node)
            if len(self.key_to_node)>self.capacity:
                back_node=self.dummy.pre
                del self.key_to_node[back_node.key]
                self.remove(back_node)
    
    def remove(self,x:ListNode)->None:
        x.pre.next=x.next
        x.next.pre=x.pre
    def put_top(self,x:ListNode)->None:
        x.pre=self.dummy
        x.next=self.dummy.next
        x.pre.next=x
        x.next.pre=x

 23.合并k个升序链表

小顶堆：首先重构链表的小于方法，__lt__，使得小顶堆可以比较链表结点的大小。遍历列表，将每个链表的 头结点加入到堆中，因为每个链表都是排好序的，所以头结点一定是最小的，然后从堆中弹出结点，如果这个结点有下一个结点，那么下一个结点也有可能是下一个较小的结点，也将其加入到堆中，然后不管该结点有没有下一给结点，都将这个结点连到我们最终的结果链表中

import heapq
class ListNode:
    def __init__(self,val=None,next=None):
        self.val=val
        self.next=next
ListNode.__lt__=lambda a,b:a.val<b.val
class solution:
    def method(self,nums):
        h=[head for head in nums if head]
        heapq.heapify(h)
        dummy=ListNode(None,head)
        cur=dummy
        while h:
            u=heapq.heappop(h)
            if u.next:
                heapq.heappush(h,u.next)
            cur.next=u
            cur=cur.next
        return dummy.next
    def toList(self,nums):
        head=ListNode(nums[0])
        cur=head
        for num in nums[1:]:
            cur.next=ListNode(num)
            cur=cur.next
        return head
    def printList(self,head):
        ans=[]
        cur=head
        while cur:
            ans.append(cur.val)
            cur=cur.next
        print(" ".join(map(str,ans)))
if __name__=="__main__":
    import sys
    n=int(sys.stdin.readline().strip())
    lists=[]
    for _ in range(n):
        nums=list(map(int,sys.stdin.readline().strip().split()))
        head=solution().toList(nums)
        lists.append(head)
    head=solution().method(lists)
    solution().printList(head)

124.二叉树中的最大路径和

可以对比543题二叉树的最大直径，思路一样，在遍历算链长的时候顺便计算最大路径和。二叉树的最大直径是和边有关，而最大路径和是和结点值有关，最大路径和等于左子树的值加右子树的值再加上当前节点的值，递归返回的值是左子树和右子树链长较大的那个值加上当前结点的值，还要和0取最大值以防加上负数，注意要初始化ans为最小负数来避免所有节点都是负数的情况。

84.柱状图中最大矩形

单调递减栈: 利用单调栈，求当前柱子的所能形成的最大矩形面积，需要找到栈口元素和左边界，如果只能栈口元素比栈顶元素小，就把栈顶元素弹出，此时的栈顶元素就是左边界，用(i-left-1)*height[idx]就是矩形的面积了。注意为了把栈中的元素全部计算，需要向height数组中加入-1，如果没有左边界的柱子，那么让左边界为-1

32.最长有效括号

栈：将括号字符串分段，当第一次出现右括号数量大于左括号数量的时候，以当前括号为界被字符串分段。遍历字符串，遇到左括号就入栈，遇到右括号就匹配，如果栈不为空，就pop，如果pop后栈为空，说明都匹配，计算长度，i-start，如果pop后栈为空，说明有不匹配的左括号，计算长度i-st[-1]，如果遇到右括号时发现栈为空，说明是右括号数量大于左括号数量，将i赋值给start