力扣2/28

确定左上角的点和右下角的点，然后缩小遍历范围，在从右往左遍历时，要判断是否还能继续遍历

返回是否是环形链表： 利用快慢指针来判断是否相遇，从而判断是否存在有环

 返回环形链表的环的第一个结点：利用一个集合来保存遍历过的结点，如果结点在集合中出现，说明有环，如果没有的话就加入到集合中去，并移动头节点

---

 利用递归，如果没有叶子节点了就返回深度，否则返回左右子树中深度更大的子树的深度

 多源bfs:先遍历整个数组，统计新鲜橘子的数量，遇到腐烂橘子就加到队列里去，然后遍历队列里的橘子，扩展到他四周的橘子，如果是新鲜的就加入到队列里去，并减少新鲜橘子的数量，队列里的全遍历一遍，耗费时间加1，最后如果还剩新鲜橘子就返回-1

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        q=deque()
        fresh=0
        directions=[[1,0],[-1,0],[0,1],[0,-1]]
        m=len(grid)
        n=len(grid[0])
        cnt=0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j]==1:
                    fresh+=1
                elif grid[i][j]==2:
                    q.append([i,j])
        while q and fresh>0:
            for i in range(len(q)):
                x,y=q.popleft()
                for dx,dy in directions:
                    nx=x+dx
                    ny=y+dy
                    if(nx>=0 and nx<m and ny>=0 and ny<n and grid[nx][ny]==1):
                        q.append([nx,ny])
                        grid[nx][ny]=2
                        fresh-=1
            cnt+=1
        if fresh>0:
            return -1
        else:
            return cnt

 

dfs:通过深搜和回溯来解决，如果当前位置字母与word的k位置字母相等，则将该位置置空，并继续搜索其四个方向是否为word的第k+1个位置，搜索完成后恢复现场。如果搜到word的最后一个位置，返回true，如果不相等返回false

 

二分查找：在一个二维矩阵中搜索某一个目标值，二维矩阵有序，可以用二分查找的方式。把二维矩阵拉成一维矩阵，一维矩阵的坐标mid对应到二维矩阵中去，横坐标等于mid//列数，纵坐标等于mid%列数。

利用栈：当遇到数字时，计算数字的大小，遇到左括号时，将当前字符串和数字压入栈内，并重置字符串和数字，遇到右括号时，从栈内弹出字符串和数字，和当前字符串res进行拼接，遇到字符时，直接拼接res

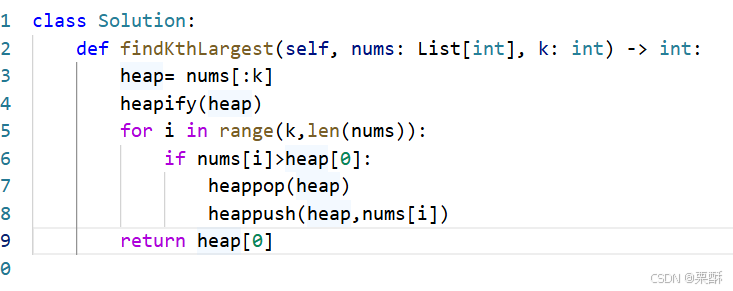
构建小顶堆：heapify（），取数组的前k个元素，再对剩余元素进行处理，大于堆顶元素就pop处理，构建大顶堆的话就把数字取负数构建小顶堆

 

小顶堆：先统计每个元素出现的频率，用字典保存，然后使用小顶堆存储键值对，只要堆的大小还小于k，就往堆里加元素，堆的大小等于k后，只要待加入的元素大于堆顶元素，就加入堆，最后输出堆里的元素

---