平衡二叉树又称 AVL树,主要的特点有:
1.任意节点的左、右子树均为AVL数。
2.根节点的左、右子树的高度差的绝对值不大于1。
要求左右子树的高度差为1,是尽量保持树的平衡使其被检索的速度达到 log n(二分查找)
int Deep_hightest(Tree root)
{
if (!root) return 0;
int l = Deep_hightest(root->left);
int r = Deep_hightest(root->right);
return (l > r ? l : r) + 1;
}想要保证一个树是平衡的,那么我们再插入的时候就要进行检测和调整,保证树的平衡。
树的平衡被破坏有四种情况:
1.被破坏的节点的左子树的左子树(该节点为空)被加入了一个节点,此时这个节点的左右高度差的绝对值如果等于2,那这个节点的平衡就被破坏了。需要将最下面的被破坏的节点进行左左旋转。

2.节点的左子树的右子树破坏了该节点(LR旋转)
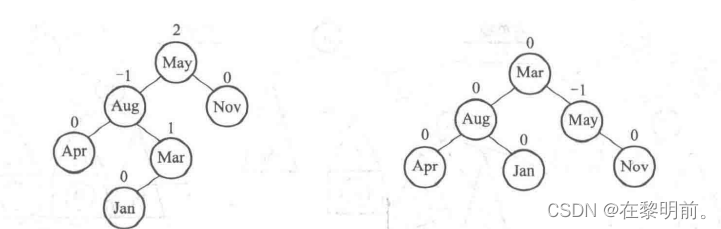
3.节点的右子树的右子树破坏了该节点的平衡(RR旋转)
4.节点的右子树的左子树破坏了该节点的平衡(RL旋转)
平衡二叉树的插入与调整
LL旋转:

将被破坏的节点用其坐子树代替,变为其左子树的右子树(平衡树将比节点小的数放在左子树,比节点大的数放在右子树)
LR旋转:
 更具平衡二叉树平衡条件,比节点小的数放在节点的左子树,比节点
更具平衡二叉树平衡条件,比节点小的数放在节点的左子树,比节点








 本文介绍了AVL树(平衡二叉树)的概念及其特点,强调了保持树平衡的重要性。详细阐述了四种可能导致平衡破坏的情况及对应的旋转调整方法:LL旋转、LR旋转、RR旋转和RL旋转。此外,还讲解了平衡二叉树的查找效率,并讨论了删除节点时如何保证树的平衡性,包括叶子节点、单子节点和双子节点删除的处理策略。欢迎留言讨论。
本文介绍了AVL树(平衡二叉树)的概念及其特点,强调了保持树平衡的重要性。详细阐述了四种可能导致平衡破坏的情况及对应的旋转调整方法:LL旋转、LR旋转、RR旋转和RL旋转。此外,还讲解了平衡二叉树的查找效率,并讨论了删除节点时如何保证树的平衡性,包括叶子节点、单子节点和双子节点删除的处理策略。欢迎留言讨论。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








