概率论基础

• 二维随机变量

二维随机变量是指一个随机实验产生的结果可以用一个有序对来描述的随机变量。它在数学上表示为(X, Y)，其中X和Y是两个单独的随机变量。

二维随机变量的取值可以是有限的、可数的或者连续的，取决于具体的情况。对于有限或可数的二维随机变量，可以通过列举每个可能的取值和对应的概率来描述其分布；对于连续的二维随机变量，可以使用概率密度函数（PDF）来描述其分布。

二维随机变量在实际应用中非常常见。例如，在统计学中，可以用二维随机变量来描述两个相关变量之间的关系；在金融学中，可以用二维随机变量来描述股票价格和时间的关系；在图像处理中，可以用二维随机变量来描述像素的位置和灰度值等。

二维随机变量是用来描述随机实验结果的有序对，它可以有不同类型的取值，并且在各种领域中有广泛的应用。

二维离散型随机变量

        若二维随机变量(X,Y)全部可能取到的不同值是有限对或可列无限对，则称(X,Y)是离散型随机变量。

        二维离散型随机变量是指在一个二维样本空间中，随机变量的取值有限且可数的情况。每个取值都有一个对应的概率，可以通过概率质量函数（PMF）来描述随机变量的分布。

举个例子，假设有一个二维离散型随机变量X，它的取值可以是{(0,0), (0,1), (1,0), (1,1)}，对应的概率分别为{0.3, 0.2, 0.4, 0.1}。这里的概率满足非负性和总和为1的条件。

二维连续型随机变量

        二维连续型随机变量是指在一个二维样本空间中，随机变量可以取到无限个可能的取值，这些取值是连续的。它的分布可以通过概率密度函数（PDF）来描述。

举个例子，假设有一个二维连续型随机变量Y，其分布可以用二维高斯分布来描述。高斯分布有两个参数，均值和协方差矩阵。通过指定这些参数，我们可以得到Y在样本空间中的分布情况。

• 边缘分布

        边缘分布是一个多维随机变量中某个特定变量（或多个特定变量）的概率分布。它表示了在考察特定变量时，其他变量的取值对其概率分布的影响被忽略掉了。

假设有一个二维随机变量 (X, Y) ，其联合概率分布已知。边缘分布可以用来描述单独某个变量的概率分布，不考虑其他变量的取值。对于 (X, Y) 中的变量 X 来说，边缘分布就是只关注 X 变量的概率分布，而将 Y 变量的取值忽略掉。类似地，可以计算出 Y 的边缘分布，不考虑 X 变量的取值。

        边缘分布可以通过对联合概率分布进行求和或积分来获得。对于离散型变量，边缘分布可以通过对联合概率质量函数（PMF）进行求和来获得；对于连续型变量，边缘分布可以通过对联合概率密度函数（PDF）进行积分来获得。

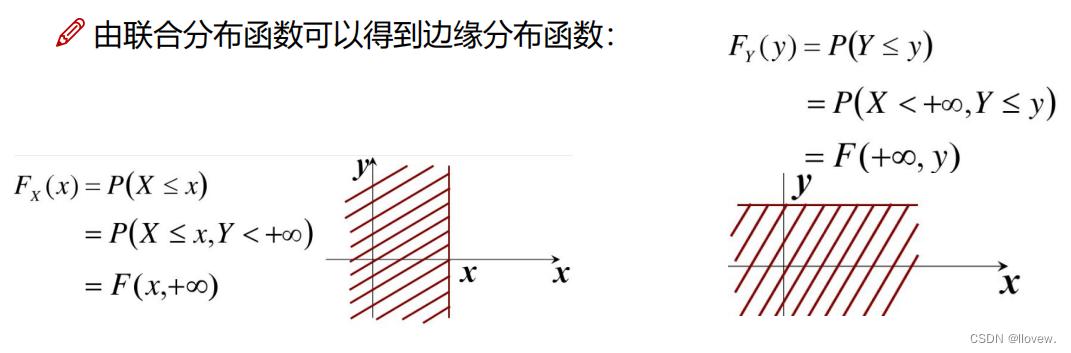
例题

• 期望

        期望是概率论和统计学中的一个重要概念，用于描述随机变量的平均值或中心位置。简而言之，期望是对随机变量的所有可能取值进行加权平均的结果。

以离散型随机变量为例，假设随机变量X可以取到的值为x1, x2, ..., xn，它们的概率分别为P(X=x1), P(X=x2), ..., P(X=xn)。则随机变量X的期望E(X)可以通过以下公式计算：

E(X) = x1 * P(X=x1) + x2 * P(X=x2) + ... + xn * P(X=xn)

期望可以理解为在多次实验中，随机变量X取值的长期平均值。它具有多种应用，例如：

1. 描述平均情况：期望可以提供随机变量的平均值，帮助我们了解数据集或概率分布的中心倾向或典型特征。

2. 决策依据：在决策问题中，期望可以被用来评估各种可能结果的价值或效用，从而帮助做出最优决策。

3. 风险评估：期望可以用于计算风险或损失的预期值，帮助进行合理的风险管理和风险评估。

4. 模型评估指标：在机器学习和统计建模中，期望可以用作评估模型预测准确性的指标，比如均方误差（MSE）或对数损失函数（log loss）等。

通过对随机变量的加权平均，帮助我们对数据和概率分布进行定量描述和分析，从而支持决策、模型评估和风险管理等。

连续型随机变量期望

二维情况

例题

数学期望的性质

• 方差

        数学期望反映了随机变量的取值水平，方差是概率论和统计学中用于描述随机变量分布分散程度的度量。它衡量随机变量的取值偏离其期望值的程度。

对于离散型随机变量X，假设它的期望值为μ。方差Var(X)可以通过以下公式计算：

Var(X) = E[(X - μ)^2] = (x1 - μ)^2 * P(X=x1) + (x2 - μ)^2 * P(X=x2) + ... + (xn - μ)^2 * P(X=xn)

其中，x1, x2, ..., xn 是随机变量X所有可能的取值，P(X=x1), P(X=x2), ..., P(X=xn)是它们对应的概率。

方差反映了随机变量取值与其期望值之间的离散程度。较大的方差意味着随机变量的取值相对于其期望值更分散，而较小的方差则表示取值相对集中。

方差具有以下特性和应用：

1. 方差非负：方差始终大于或等于零。

2. 方差为零：当且仅当随机变量的取值全部等于其期望值时，方差为零。

3. 方差用于衡量数据的波动性和散布程度，对于评估数据的不确定性和预测能力很有用。

4. 方差是许多统计推断和参数估计方法的基础，例如最小二乘法。

通过计算方差，我们可以量化随机变量的分散程度，并使用它来比较不同分布或数据集的变异性。方差与期望一起提供了对随机变量分布中心和分散程度的完整描述。

大数定理

大数定律（Law of Large Numbers）是概率论中一个重要的定理，它指出随着样本数量的增加，样本均值会趋近于总体均值。换句话说，当我们从一个总体中抽取足够多的样本时，这些样本的平均值会接近于整个总体的平均值。

随着样本数量的增加，样本的平均值将不断接近于总体的期望（也就是平均值）。这意味着我们可以通过对足够多的样本进行观察和分析，来推测总体的性质。

这个定律在机器学习中非常有用。在训练模型时，我们通常使用一个代表性的训练数据集来估计模型的参数。大数定律的思想告诉我们，当训练数据足够大时，模型的参数估计会趋近于真实的参数值。因此，使用更多的训练样本可以提高模型的准确性和稳定性。

总而言之，大数定律告诉我们，通过增加样本数量，我们可以更好地了解总体的特征，并基于此进行推断和预测。

马尔可夫不等式

马尔可夫不等式（Markov's inequality）是概率论中的一个重要不等式，它提供了一个上界，用于估计一个非负随机变量关于其期望值的概率

具体而言，对于一个非负的随机变量X和任意正数a，马尔可夫不等式给出了以下不等式：

P(X >= a) <= E(X) / a

其中，P(X >= a)表示随机变量X大于等于a的概率，E(X)表示X的期望值。

马尔可夫不等式的直观解释是，对于一个非负随机变量X，它的概率质量主要集中在其期望值附近。因此，我们可以使用期望值来估计随机变量X超过某个给定值的概率上界。

举个例子，假设我们有一个非负随机变量X，其期望值为10。然后我们想要估计X大于等于20的概率上界。根据马尔可夫不等式，我们可以得到以下不等式：

P(X >= 20) <= E(X) / 20 = 10 / 20 = 0.5

这意味着X大于等于20的概率不会超过0.5。

马尔可夫不等式在概率论和统计学中非常有用，它可以帮助我们对随机变量的概率分布进行初步估计和分析，尤其是当我们缺乏具体分布信息时。然而，要注意的是，马尔可夫不等式提供的是一个上界，可能会比实际概率较松。

切比雪夫不等式

切比雪夫不等式（Chebyshev's inequality），它提供了一个上界，用于估计一个随机变量与其期望值偏离一定范围的概率。切比雪夫不等式在概率论和统计学中非常有用，它可以帮助我们对随机变量的偏离程度进行估计和分析，而不需要对具体的分布形式做出任何假设。然而，要注意的是，切比雪夫不等式提供的是一个上界，可能会比实际概率较松。

对于任意一个随机变量X和任意正数k，切比雪夫不等式给出了以下不等式：

P(|X - μ| >= kσ) <= 1/k^2

其中，P(|X - μ| >= kσ)表示随机变量X与其期望值μ偏离超过k个标准差的概率，σ表示X的标准差。

切比雪夫不等式的直观解释是，对于任意的随机变量，无论其具体的分布形式如何，其与其期望值的偏离程度受限。k值越大，偏离的概率越小。

举个例子，假设我们有一个随机变量X，其期望值为10，标准差为2。我们想要估计X与期望值偏离超过6个标准差的概率上界。根据切比雪夫不等式，我们可以得到以下不等式：

P(|X - 10| >= 6*2) <= 1/(6^2) = 1/36

这意味着X与其期望值偏离超过12的概率不会超过1/36。

中心极限定理

中心极限定理是一个重要的统计学概念，它描述了一种现象：当我们从一个总体中随机抽取许多样本，并计算每个样本的平均值，这些平均值的分布将趋向于正态分布，即使总体分布不是正态分布。中心极限定理告诉我们，当样本数量足够大时，样本的平均值就会呈现出正态分布的特征，不论原始总体是什么分布形式。这个定理在机器学习中非常有用，因为它允许我们使用正态分布的一些性质来进行推断和建模。

中心极限定理可以帮助我们估计总体的平均值和标准差，通过从总体中抽取多个样本并计算它们的平均值，我们可以得到一个样本均值的分布，该分布趋近于正态分布。我们可以使用这个样本均值的分布来进行假设检验、置信区间估计等统计推断。

小工具：Sampling Distributions

模型比较

最大似然

最大似然（Maximum Likelihood）是一种统计方法，用于估计模型的参数。它基于观测数据，通过寻找最有可能产生观测数据的参数值来确定最佳参数。最大似然的思想是认为观测数据是由已知模型生成的，通过在给定数据集上最大化似然函数的值，我们可以找到最好的参数估计。

奥卡姆剃刀

奥卡姆剃刀（Occam's Razor）是一种选择模型的原则，它认为在解释数据的不确定性时，越简单的模型越好。奥卡姆剃刀的核心思想是，如果两个模型能够解释观测数据的情况下，我们更应该选择解释更简单的模型，因为它更具有泛化能力，并且更不容易受到噪声数据的影响。

在模型比较中，最大似然和奥卡姆剃刀可以联系起来。最大似然方法通过最大化观测数据的可能性来选择最佳参数，而奥卡姆剃刀则通过选择最简单的模型来解释数据。在实际应用中，我们常常需要权衡两个因素：模型的复杂度和对数据的拟合程度。最大似然提供了一种评估模型拟合能力的指标，而奥卡姆剃刀则提供了一种选择最简单模型的原则。