目录
2、计算数值型特征与类别型特征之间相关性的方法:Eta^2 (Correlation Ratio) 相关比
(1)Eta² (Correlation Ratio) 计算原理
步骤 1:计算总变异(Total Sum of Squares,)
步骤 2:计算组间变异(Between-group Sum of Squares,)
本文理论部分:
零、数据集介绍
本文使用从 Data Hackathon 3.x AV hackathon 中获取数据集,数据集介绍:
Data Hackathon 3.x 是由 Analytics Vidhya 主办的一次数据科学竞赛,旨在为全球的数据科学家提供一个展示技能的平台。
- ID:每条记录的唯一标识符。
- Gender:申请人的性别。
- City:申请人所在城市。
- Monthly_Income:申请人的月收入。
- DOB (Date of Birth):申请人的出生日期。
- Lead_Creation_Date:申请人提交信息的日期。
- Loan_Amount_Applied:申请人申请的贷款金额。
- Loan_Tenure_Applied:申请贷款的期限(年数)。
- Existing_EMI:已有的每月等额还款(EMI),如果有的话。
- Employer_Name:申请人所在公司的名称。
- Interest_Rate:贷款的利率(如果有)。
- Processing_Fee:贷款处理费(如果有)。
- EMI_Loan_Submitted:已提交的贷款EMI(如果有的话)。
- Filled_Form:是否填写了申请表(Y/N)。
- Device_Type:申请表提交时使用的设备类型。
- Var2, Var4:可能是编码的其他变量。
- Source:申请的来源(可能是在线或线下)。
- LoggedIn:申请人是否在提交时登录。
- Disbursed:贷款是否已发放(0 表示未发放,1 表示已发放)。
这个数据集可以用于分析贷款批准或发放的趋势,预测哪些申请可能会成功,或评估影响贷款批准的因素。
一、数据探索
1、对特征类型的探索
可通过肉眼观察,在示例数据集中:
连续型数值特征:
- Monthly_Income:月收入
- Loan_Amount_Applied:申请的贷款金额
- Loan_Tenure_Applied:贷款申请期限
- Existing_EMI:现有的等额月供(EMI)
- Var5:其他数值特征(可能是编码值)
- Loan_Amount_Submitted:提交的贷款金额
- Loan_Tenure_Submitted:提交的贷款期限
- Interest_Rate:贷款利率
- Processing_Fee:贷款处理费
- EMI_Loan_Submitted:已提交的EMI金额
- Var4:其他数值特征(可能是编码值)
- LoggedIn:是否已登录(0或1)
- Disbursed:贷款是否发放(0或1)
离散型/类别型特征:
- ID:唯一标识符
- Gender:性别
- City:城市
- DOB:出生日期
- Lead_Creation_Date:潜在客户创建日期
- Employer_Name:雇主名称
- Salary_Account:工资账户
- Mobile_Verified:手机号是否验证
- Var1:可能是编码变量
- Filled_Form:是否填写了申请表
- Device_Type:设备类型
- Var2:可能是编码变量
- Source:申请来源
数据集导入:
# Import libraries
from google.colab import files
import pandas as pd
import numpy as np
from sklearn.ensemble import GradientBoostingClassifier # GBM algorithm
from sklearn.model_selection import cross_val_score, GridSearchCV # Cross-validation and grid search
from sklearn import metrics # Additional sklearn functions
import matplotlib.pyplot as plt # Note: corrected to "pyplot" for consistency
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 4# Load dataset
# 上传文件
uploaded = files.upload()
# 检查上传的文件名
print(uploaded.keys())import chardet
# 检测文件编码
with open('Train_nyOWmfK.csv', 'rb') as f:
rawdata = f.read()
result = chardet.detect(rawdata)
print(result)# 使用检测到的编码读取文件
train = pd.read_csv('Train_nyOWmfK.csv', encoding=result['encoding'])
print(train.head())
print(train.info())2、缺失值
(1)统计各个特征具有的缺失值的数量
# Check for missing values in each column
missing_values = train.isnull().sum()
# Display columns with missing values
print(missing_values[missing_values > 0])输出结果为:

(2)删掉缺失值超过50%的特征
# Calculate the percentage of missing values in each column
missing_percentage = train.isnull().mean() * 100
# Drop columns where the percentage of missing values exceeds 50%
columns_to_drop = missing_percentage[missing_percentage > 50].index
train_cleaned_1 = train.drop(columns=columns_to_drop)
print(train.shape)
print(train_cleaned_1.shape)输出结果为:(删掉了三行)
(87020, 26)
(87020, 23)(3)对连续数值类型特征进行平均值填充
# Fill missing values in the 'Loan_Tenure_Applied' column with its mean value
train_cleaned_1['Loan_Amount_Applied'] = train_cleaned_1['Loan_Amount_Applied'].fillna(train_cleaned_1['Loan_Amount_Applied'].mean())
train_cleaned_1['Loan_Tenure_Applied'] = train_cleaned_1['Loan_Tenure_Applied'].fillna(train_cleaned_1['Loan_Tenure_Applied'].mean())
train_cleaned_1['Existing_EMI'] = train_cleaned_1['Existing_EMI'].fillna(train_cleaned_1['Existing_EMI'].mean())
train_cleaned_1['Loan_Amount_Submitted'] = train_cleaned_1['Loan_Amount_Submitted'].fillna(train_cleaned_1['Loan_Amount_Submitted'].mean())
train_cleaned_1['Loan_Tenure_Submitted'] = train_cleaned_1['Loan_Tenure_Submitted'].fillna(train_cleaned_1['Loan_Tenure_Submitted'].mean())
# Verify if there are any remaining missing values
missing_values = train_cleaned_1.isnull().sum()
print(missing_values[missing_values > 0])输出结果为:(仅剩余三个类别型特征没有进行缺失值填充)
City 1003
Employer_Name 71
Salary_Account 11764
dtype: int64(4)对类别类型特征进行众数填充
# Fill missing values with its mode (most frequent value)
train_cleaned_1['City'] = train_cleaned_1['City'].fillna(train_cleaned_1['City'].mode()[0])
train_cleaned_1['Employer_Name'] = train_cleaned_1['Employer_Name'].fillna(train_cleaned_1['Employer_Name'].mode()[0])
train_cleaned_1['Salary_Account'] = train_cleaned_1['Salary_Account'].fillna(train_cleaned_1['Salary_Account'].mode()[0])
# Verify if there are any remaining missing values
missing_values = train_cleaned_1.isnull().sum()
print(missing_values[missing_values > 0])输出结果为:(所有特征都没有缺失值了)
Series([], dtype: int64)3、特征/目标分布的可视化
(1)目标变量(Disbursed)分布可视化
由于 Disbursed 是二分类标签,可以通过柱状图或饼图来查看标签的分布情况,观察是否存在类别不平衡的情况(例如 0 类和 1 类的样本数是否相差很大)。
import matplotlib.pyplot as plt
data = train_cleaned_1
data['Disbursed'].value_counts().plot(kind='bar')
plt.title('Disbursed Distribution')
plt.xlabel('Loan Disbursed (0=No, 1=Yes)')
plt.ylabel('Count')
plt.show()输出结果为:

(2)数值特征分布可视化
以两个特征为例:(Monthly_Income、Loan_Amount_Applied)
# 过滤掉异常大的收入值(例如,收入超过一定阈值的可能是错误数据)
# 假设合理的 Monthly_Income 范围在 0 到 800,000 之间,可以根据实际情况调整
cleaned_data = data[data['Monthly_Income'] < 800000]
# 绘制清洗后的 'Monthly_Income' 列的直方图
plt.figure(figsize=(8,6))
plt.hist(cleaned_data['Monthly_Income'], bins=30, color='blue', edgecolor='black')
plt.title('Histogram of Cleaned Monthly Income')
plt.xlabel('Monthly Income')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()输出结果为:

# 过滤掉异常大的收入值(例如,超过一定阈值的可能是错误数据)
# 假设合理的 Loan_Amount_Applied 范围在 0 到 1,000,000 之间,可以根据实际情况调整
cleaned_data_2 = data[data['Loan_Amount_Applied'] < 1000000]
# 绘制清洗后的 'Loan_Amount_Applied' 列的直方图
plt.figure(figsize=(8,6))
plt.hist(cleaned_data_2['Loan_Amount_Applied'], bins=30, color='blue', edgecolor='black')
plt.title('Histogram of Cleaned Loan_Amount_Applied')
plt.xlabel('Loan_Amount_Applied')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()输出结果为:

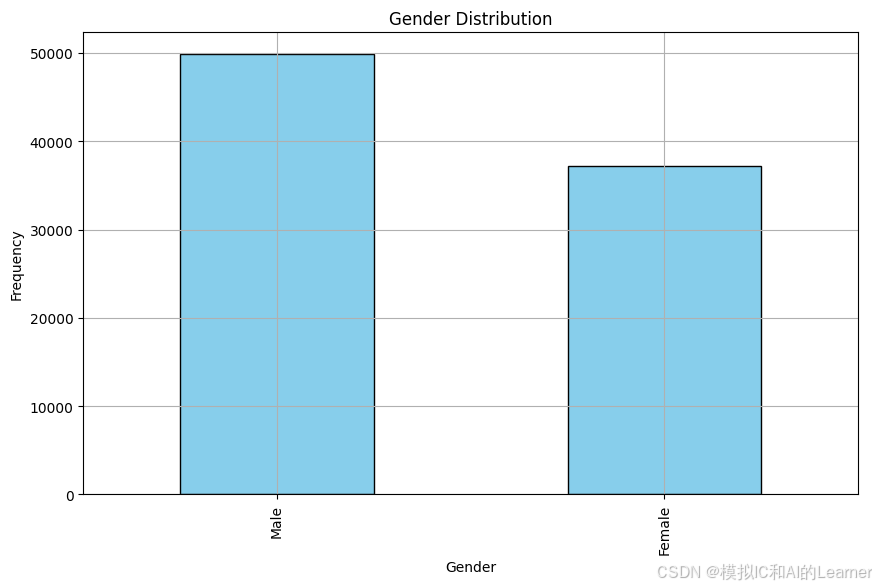
(3)类别特征分布可视化
import matplotlib.pyplot as plt
import pandas as pd
# 假设你已经加载了数据集并进行缺失值填充
# 填充缺失值(使用众数填充)
# 获取 Gender 列的频次分布
Gender_counts = data['Gender'].value_counts()
# 绘制 Gender 列的条形图
plt.figure(figsize=(10,6))
Gender_counts.plot(kind='bar', color='skyblue', edgecolor='black')
plt.title('Gender Distribution')
plt.xlabel('Gender')
plt.ylabel('Frequency')
plt.xticks(rotation=90)
plt.grid(True)
plt.show()
输出结果为:
4、特征/目标的分布相关的统计量
(1)连续型特征分布相关的统计量
连续型特征有:均值、中值、众数;方差、四分位数间距。
import pandas as pd
from scipy import stats
# 计算 Monthly_Income 的各项统计量
# 计算均值
mean_income = data['Monthly_Income'].mean()
# 计算中值
median_income = data['Monthly_Income'].median()
# 计算众数
mode_income = data['Monthly_Income'].mode()[0]
# 计算方差
variance_income = data['Monthly_Income'].var()
# 计算四分位数间距 (IQR)
iqr_income = stats.iqr(data['Monthly_Income'])
# 打印结果
print(f"Mean of Monthly Income: {mean_income}")
print(f"Median of Monthly Income: {median_income}")
print(f"Mode of Monthly Income: {mode_income}")
print(f"Variance of Monthly Income: {variance_income}")
print(f"Interquartile Range (IQR) of Monthly Income: {iqr_income}")输出结果为:
Mean of Monthly Income: 58849.97435072397
Median of Monthly Income: 25000.0
Mode of Monthly Income: 25000
Variance of Monthly Income: 4741555729007.092
Interquartile Range (IQR) of Monthly Income: 23500.0(2)类别型特征分布相关的统计量
类别型特征分布相关的统计量有:频次分布、相对频率、众数、频率表、熵、基尼指数
- 频次分布(Frequency Distribution):用
value_counts()获取每个类别的出现次数。 - 相对频率(Relative Frequency):用
value_counts(normalize=True)获取各类别的比例。 - 众数(Mode):用
mode()获取出现次数最多的类别。 - 频率表(Contingency Table):如果有多个类别变量可以计算其交叉分布,但在这里只涉及单一的
City列,默认就是value_counts()。 - 熵(Entropy):我们可以使用信息论中的熵公式来计算类别变量的熵。
- 基尼指数(Gini Index):计算类别变量的基尼指数。
import pandas as pd
import numpy as np
from scipy.stats import entropy
# 假设你已经加载了数据集并进行缺失值处理
# 填充缺失值
data['City'] = data['City'].fillna(data['City'].mode()[0])
# 1. 频次分布
freq_dist = data['City'].value_counts()
# 2. 相对频率
relative_freq = data['City'].value_counts(normalize=True)
# 3. 众数
mode_city = data['City'].mode()[0]
# 4. 频率表 (对于单个变量就是频次分布)
# 这里只计算 City 列的频率表
contingency_table = pd.crosstab(index=data['City'], columns='Count')
# 5. 熵 (计算类别型变量的熵)
# 首先计算类别的概率分布
probabilities = relative_freq / relative_freq.sum()
city_entropy = entropy(probabilities, base=2)
# 6. 基尼指数
# 基尼指数公式为: 1 - sum(p_i^2),其中 p_i 是类别i的概率
gini_index = 1 - sum(probabilities**2)
# 打印结果
print("Frequency Distribution:\n", freq_dist)
print("\nRelative Frequency:\n", relative_freq)
print("\nMode of City:", mode_city)
print("\nContingency Table:\n", contingency_table)
print("\nEntropy of City:", city_entropy)
print("\nGini Index of City:", gini_index)输出结果为:
Frequency Distribution:
City
Delhi 13530
Bengaluru 10824
Mumbai 10795
Hyderabad 7272
Chennai 6916
...
Lalitpur 1
Kandhamal 1
Sawai Madhopur 1
Munger 1
Lohit 1
Name: count, Length: 697, dtype: int64
Relative Frequency:
City
Delhi 0.155481
Bengaluru 0.124385
Mumbai 0.124052
Hyderabad 0.083567
Chennai 0.079476
...
Lalitpur 0.000011
Kandhamal 0.000011
Sawai Madhopur 0.000011
Munger 0.000011
Lohit 0.000011
Name: proportion, Length: 697, dtype: float64
Mode of City: Delhi
Contingency Table:
col_0 Count
City
ADIPUR 7
AHMEDB 9
AMALSAD 2
ANJAR 6
Abohar 6
... ...
West Singhbhum 14
Yadgir 5
Yamuna Nagar 28
Yavatmal 15
sri ganganagar 8
[697 rows x 1 columns]
Entropy of City: 5.11431277241882
Gini Index of City: 0.92498062140906925、Pandas支持的统计量
6、特征之间的相关性
(1)数值型 与 数值型
数值型特征为:(选4个为例)
numeric_features = ['Monthly_Income', 'Loan_Amount_Applied', 'Loan_Tenure_Applied', 'Existing_EMI']相关矩阵计算:
import pandas as pd
# 假设 data 是你的 DataFrame,其中 f, g, h, i, j, k, l 是数值型
numeric_features = ['Monthly_Income', 'Loan_Amount_Applied', 'Loan_Tenure_Applied', 'Existing_EMI']
# 1) 使用 Pearson 相关系数
corr_pearson = data[numeric_features].corr(method='pearson')
# 2) 使用 Spearman 相关系数
corr_spearman = data[numeric_features].corr(method='spearman')
print("Pearson相关系数矩阵:\n", corr_pearson)
print("Spearman相关系数矩阵:\n", corr_spearman)
输出结果为:
Pearson相关系数矩阵:
Monthly_Income Loan_Amount_Applied Loan_Tenure_Applied \
Monthly_Income 1.000000 0.003050 -0.004282
Loan_Amount_Applied 0.003050 1.000000 0.502259
Loan_Tenure_Applied -0.004282 0.502259 1.000000
Existing_EMI 0.135973 0.064065 0.054314
Existing_EMI
Monthly_Income 0.135973
Loan_Amount_Applied 0.064065
Loan_Tenure_Applied 0.054314
Existing_EMI 1.000000
Spearman相关系数矩阵:
Monthly_Income Loan_Amount_Applied Loan_Tenure_Applied \
Monthly_Income 1.000000 0.284490 0.132636
Loan_Amount_Applied 0.284490 1.000000 0.771356
Loan_Tenure_Applied 0.132636 0.771356 1.000000
Existing_EMI 0.170184 0.401722 0.372332
Existing_EMI
Monthly_Income 0.170184
Loan_Amount_Applied 0.401722
Loan_Tenure_Applied 0.372332
Existing_EMI 1.000000
(2)类别型 与 类别型
类别型特征为:(选3个为例)
categorical_features = ['Gender', 'City', 'Var1']需要一个类似于相关系数(在 0~1 之间)的度量,可以使用 Cramér’s V。它基于卡方统计量,能够一定程度上量化类别型特征之间的相关强度,值越接近 1 表示相关度越高。
import numpy as np
from scipy.stats import chi2_contingency
def cramers_v(confusion_matrix):
""" 计算列联表的 Cramér's V. """
chi2 = chi2_contingency(confusion_matrix)[0]
n = confusion_matrix.sum().sum()
r, k = confusion_matrix.shape
return np.sqrt((chi2 / n) / (min(r-1, k-1)))
categorical_features = ['Gender', 'City', 'Var1']
cramers_v_dict = {}
for i in range(len(categorical_features)):
for j in range(i+1, len(categorical_features)):
feature1 = categorical_features[i]
feature2 = categorical_features[j]
cm = pd.crosstab(data[feature1], data[feature2])
cv = cramers_v(cm)
cramers_v_dict[(feature1, feature2)] = cv
print(cramers_v_dict)
输出结果为:
{('Gender', 'City'): 0.1557702945225498,
('Gender', 'Var1'): 0.4111890284727607,
('City', 'Var1'): 0.12985298162486653}
(3)数值型 与 类别型
Correlation Ratio(相关比) 又称 η (eta),是数值型变量对于分类变量的“解释程度”。
import numpy as np
def correlation_ratio(cat, val):
"""
cat: 类别型数据 (array-like)
val: 数值型数据 (array-like)
"""
# 将数据转换为 array,保证索引对齐
cat = np.array(cat)
val = np.array(val)
# 整体平均值
mean = val.mean()
categories = np.unique(cat)
ss_between = 0.0
ss_total = 0.0
for c in categories:
# 当前类别内所有数值
vals_c = val[cat == c]
# 当前类别内平均值
mean_c = vals_c.mean()
ss_between += len(vals_c) * (mean_c - mean) ** 2
ss_total = ((val - mean)**2).sum()
eta_squared = ss_between / ss_total if ss_total != 0 else 0
return np.sqrt(eta_squared)
categorical_features = ['Gender', 'City', 'Var1']
numeric_features = ['Monthly_Income', 'Loan_Amount_Applied', 'Loan_Tenure_Applied', 'Existing_EMI']
corr_ratio_dict = {}
for cat_feature in categorical_features:
for num_feature in numeric_features:
eta = correlation_ratio(data[cat_feature], data[num_feature])
corr_ratio_dict[(cat_feature, num_feature)] = eta
print(corr_ratio_dict)
输出结果为:
{('Gender', 'Monthly_Income'): 0.011183206512192567,
('Gender', 'Loan_Amount_Applied'): 0.03222758535635746,
('Gender', 'Loan_Tenure_Applied'): 0.09937326653628076,
('Gender', 'Existing_EMI'): 0.02870818495014723,
('City', 'Monthly_Income'): 0.047788105917965874,
('City', 'Loan_Amount_Applied'): 0.19270655982880858,
('City', 'Loan_Tenure_Applied'): 0.25029451138066255,
('City', 'Existing_EMI'): 0.0315829531080445,
('Var1', 'Monthly_Income'): 0.013968048822778106,
('Var1', 'Loan_Amount_Applied'): 0.12556309523665257,
('Var1', 'Loan_Tenure_Applied'): 0.1447229494853945,
('Var1', 'Existing_EMI'): 0.033461833371721185}
(4)综合计算所有特征之间的相关性(热力图)
所有特征之间的相关性矩阵,且不区分数值型和类别型特征,以下是一个更新版的函数,能够处理所有特征之间的相关性。具体地:
- 数值型 vs 数值型:使用 Pearson 相关系数(你也可以选择 Spearman)
- 类别型 vs 类别型:使用 Cramér's V
- 数值型 vs 类别型:使用 Correlation Ratio (η)
import numpy as np
import pandas as pd
from scipy.stats import chi2_contingency
def cramers_v(confusion_matrix):
""" 计算列联表的 Cramér's V """
chi2 = chi2_contingency(confusion_matrix)[0]
n = confusion_matrix.sum().sum()
r, k = confusion_matrix.shape
if n == 0 or min(r-1, k-1) == 0:
return 0.0
return np.sqrt((chi2 / n) / (min(r - 1, k - 1)))
def correlation_ratio(cat, val):
""" 计算类别型特征与数值型特征之间的 Correlation Ratio (η) """
cat = np.array(cat)
val = np.array(val)
# 全部数值的均值
overall_mean = np.nanmean(val)
# 处理NaN值
not_nan_mask = ~np.isnan(val)
cat = cat[not_nan_mask]
val = val[not_nan_mask]
ss_total = np.sum((val - overall_mean)**2)
if ss_total == 0:
return 0.0
categories = pd.unique(cat)
ss_between = 0.0
for c in categories:
vals_c = val[cat == c]
mean_c = np.mean(vals_c)
ss_between += len(vals_c) * (mean_c - overall_mean)**2
eta_squared = ss_between / ss_total
return np.sqrt(eta_squared)
def mixed_corr_matrix(df, method_num='pearson'):
"""
计算所有特征之间的相关度矩阵,包括类别型与数值型的相关度。
- df: 包含所有数据的DataFrame
- method_num: 数值型特征之间使用的相关系数(默认 'pearson',可选择 'spearman')
"""
# 获取特征列表
features = df.columns.tolist()
# 初始化 相关度矩阵
n = len(features)
corr_mat = np.zeros((n, n))
# 构建 行列索引
feature_index = {f: idx for idx, f in enumerate(features)}
for f1 in features:
for f2 in features:
i = feature_index[f1]
j = feature_index[f2]
if j < i:
continue
# 如果是同一特征,相关度为1
if f1 == f2:
corr_mat[i, j] = 1.0
continue
# 判断特征类型
is_f1_cat = df[f1].dtype == 'object' or df[f1].dtype.name == 'category'
is_f2_cat = df[f2].dtype == 'object' or df[f2].dtype.name == 'category'
if is_f1_cat and is_f2_cat:
# 类别型 vs 类别型 -> Cramér's V
confusion_mtx = pd.crosstab(df[f1], df[f2])
value = cramers_v(confusion_mtx)
elif not is_f1_cat and not is_f2_cat:
# 数值型 vs 数值型 -> Pearson or Spearman
value = df[[f1, f2]].corr(method=method_num).iloc[0, 1]
if pd.isnull(value):
value = 0.0
else:
# 类别型 vs 数值型 -> Correlation Ratio
if is_f1_cat and not is_f2_cat:
value = correlation_ratio(df[f1], df[f2])
else:
# f2 是类别型,f1 是数值型
value = correlation_ratio(df[f2], df[f1])
corr_mat[i, j] = value
corr_mat[j, i] = value # 确保矩阵是对称的
# 返回结果为 DataFrame 格式
corr_df = pd.DataFrame(corr_mat, index=features, columns=features)
return corr_df
调用函数:
# 类别型、数值型特征的区分
categorical_features = ['Gender', 'City', 'Var1']
numeric_features = ['Monthly_Income', 'Loan_Amount_Applied', 'Loan_Tenure_Applied', 'Existing_EMI']
data1=data[categorical_features + numeric_features]
# 假设你的 DataFrame 名称是 data
corr_matrix = mixed_corr_matrix(df=data1, method_num='pearson') # 或 'spearman'
# 输出相关度矩阵
print(corr_matrix)输出结果为:
Gender City Var1 Monthly_Income \
Gender 1.000000 0.155770 0.411189 0.011183
City 0.155770 1.000000 0.129853 0.047788
Var1 0.411189 0.129853 1.000000 0.013968
Monthly_Income 0.011183 0.047788 0.013968 1.000000
Loan_Amount_Applied 0.032228 0.192707 0.125563 0.003050
Loan_Tenure_Applied 0.099373 0.250295 0.144723 -0.004282
Existing_EMI 0.028708 0.031583 0.033462 0.135973
Loan_Amount_Applied Loan_Tenure_Applied Existing_EMI
Gender 0.032228 0.099373 0.028708
City 0.192707 0.250295 0.031583
Var1 0.125563 0.144723 0.033462
Monthly_Income 0.003050 -0.004282 0.135973
Loan_Amount_Applied 1.000000 0.502259 0.064065
Loan_Tenure_Applied 0.502259 1.000000 0.054314
Existing_EMI 0.064065 0.054314 1.000000
绘制热力图:
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 设置图像大小
plt.figure(figsize=(12, 8))
# 绘制热力图
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt='.2f', linewidths=0.5, cbar=True)
# 设置标题
plt.title('corr_matrix Heatmap')
# 显示图像
plt.show()

7、特征与目标之间的关系
特征与目标的相关性可参照特征之间相关性进行计算。
(1)特征与目标之间散点图绘制
import matplotlib.pyplot as plt
# 筛选特征 Monthly_Income 小于 800000 的样本
filtered_data = data[data['Monthly_Income'] < 800000]
# Monthly_Income 是特征列名,Disbursed 是目标变量名
plt.scatter(filtered_data['Monthly_Income'], filtered_data['Disbursed'], alpha=0.6)
# 设置标题和标签
plt.title('Scatter Plot: Monthly_Income vs Disbursed')
plt.xlabel('Feature Monthly_Income')
plt.ylabel('Disbursed Variable')
# 显示图形
plt.show()

二、特征工程——数据预处理
这个部分仍然以上面的数据集为例子。
1、数值型特征处理
(1)log变换
对特征Loan_Amount_Submitted进行log变换:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 假设你的数据集是data
# 如果数据中有零或负值,需要处理(这里做简单的处理,将0或负值替换为NaN)
data['Loan_Amount_Submitted'] = data['Loan_Amount_Submitted'].replace(0, np.nan)
data['Loan_Amount_Submitted'] = data['Loan_Amount_Submitted'].replace([np.inf, -np.inf], np.nan)
# 对Loan_Amount_Submitted列进行log变换
data['Loan_Amount_Submitted_log'] = np.log(data['Loan_Amount_Submitted'])
# 设置画布
plt.figure(figsize=(12, 6))
# 变换前的直方图
plt.subplot(1, 2, 1)
plt.hist(data['Loan_Amount_Submitted'].dropna(), bins=30, color='blue', alpha=0.7)
plt.title('Histogram of Loan_Amount_Submitted (Before Log Transformation)')
plt.xlabel('Loan Amount Submitted')
plt.ylabel('Frequency')
# 变换后的直方图
plt.subplot(1, 2, 2)
plt.hist(data['Loan_Amount_Submitted_log'].dropna(), bins=30, color='green', alpha=0.7)
plt.title('Histogram of Loan_Amount_Submitted (After Log Transformation)')
plt.xlabel('Log(Loan Amount Submitted)')
plt.ylabel('Frequency')
# 展示图像
plt.tight_layout()
plt.show()
输出结果为:

(2)区间量化(分箱)
对特征 Loan_Amount_Applied 进行分箱:
使用 cut 方法(按固定区间分箱):
import pandas as pd
import numpy as np
# 假设你的数据集是data
# 定义分箱的区间,例如将数据分为5个区间
bins = [0, 500000, 1000000, 1500000, 2000000, 2500000] # 根据你的数据分配区间
# 使用cut方法进行分箱
data['Loan_Amount_Applied_binned'] = pd.cut(data['Loan_Amount_Applied'], bins=bins, labels=['0-500000', '500000-1000000', '1000000-1500000', '1500000-2000000', '2000000-2500000'], right=False)
# 显示结果
print(data[['Loan_Amount_Applied', 'Loan_Amount_Applied_binned']].head())输出结果为:
Loan_Amount_Applied Loan_Amount_Applied_binned
0 300000.0 0-500000
1 200000.0 0-500000
2 600000.0 500000-1000000
3 1000000.0 1000000-1500000
4 500000.0 500000-1000000使用 qcut 方法(按等频分箱):
import pandas as pd
import numpy as np
# 假设你的数据集是data
# 使用qcut方法进行等频分箱,例如分成5个区间
data['Loan_Amount_Applied_binned'] = pd.qcut(data['Loan_Amount_Applied'], q=5, labels=['Q1', 'Q2', 'Q3', 'Q4', 'Q5'])
# 显示结果
print(data[['Loan_Amount_Applied', 'Loan_Amount_Applied_binned']].head())输出结果为:
Loan_Amount_Applied Loan_Amount_Applied_binned
0 300000.0 Q3
1 200000.0 Q2
2 600000.0 Q5
3 1000000.0 Q5
4 500000.0 Q4(3)数据缩放:取值范围缩放、规范化
对特征 Loan_Amount_Applied 进行规范化(标准化),通常可以通过两种方式:
- 最小-最大规范化(Min-Max Scaling):将数据按比例缩放到一个特定的区间(通常是 [0, 1])。
- 标准化(Standardization):将数据按特征的均值和标准差转换,使其具有 0 的均值和 1 的标准差。
下面我会分别展示这两种方法的代码:
最小-最大规范化(Min-Max Scaling)
使用 MinMaxScaler 将数据压缩到 [0, 1] 范围内。
from sklearn.preprocessing import MinMaxScaler
# 假设你的数据集是data
scaler = MinMaxScaler()
# 对Loan_Amount_Applied进行最小-最大规范化
data['Loan_Amount_Applied_scaled'] = scaler.fit_transform(data[['Loan_Amount_Applied']])
# 显示结果
print(data[['Loan_Amount_Applied', 'Loan_Amount_Applied_scaled']].head())
输出结果为:
Loan_Amount_Applied Loan_Amount_Applied_scaled
0 300000.0 0.03
1 200000.0 0.02
2 600000.0 0.06
3 1000000.0 0.10
4 500000.0 0.05标准化(Standardization)
使用 StandardScaler 将数据标准化,使得数据的均值为0,标准差为1。
from sklearn.preprocessing import StandardScaler
# 假设你的数据集是data
scaler = StandardScaler()
# 对Loan_Amount_Applied进行标准化
data['Loan_Amount_Applied_standardized'] = scaler.fit_transform(data[['Loan_Amount_Applied']])
# 显示结果
print(data[['Loan_Amount_Applied', 'Loan_Amount_Applied_standardized']].head())
输出结果为:
Loan_Amount_Applied Loan_Amount_Applied_standardized
0 300000.0 -0.115500
1 200000.0 -0.375263
2 600000.0 0.663789
3 1000000.0 1.702841
4 500000.0 0.404026
2、类别型特征编码
(1)标签编码
标签编码将类别特征转换为整数标签。每个不同的类别将被赋予一个唯一的整数。
from sklearn.preprocessing import LabelEncoder
# 假设你的数据集是data
label_encoder = LabelEncoder()
# 对Var1进行标签编码
data['Var1_label_encoded'] = label_encoder.fit_transform(data['Var1'])
# 显示结果
print(data[['Var1', 'Var1_label_encoded']].head())输出结果为:
Var1 Var1_label_encoded
0 HBXX 13
1 HBXA 8
2 HBXX 13
3 HBXX 13
4 HBXX 13(2)独热编码
独热编码通过为每个类别创建一个新的二进制特征(列),每一行的特征值为1或0,表示是否属于该类别。
# 使用pandas的get_dummies进行独热编码
data_encoded = pd.get_dummies(data['Var1'], prefix='Var1')
# 将独热编码结果合并到原始数据集
data = pd.concat([data, data_encoded], axis=1)
# 显示结果
print(data[['Var1'] + list(data_encoded.columns)].head())输出结果为:
Var1 Var1_HAVC Var1_HAXA Var1_HAXB Var1_HAXC Var1_HAXF Var1_HAXM \
0 HBXX False False False False False False
1 HBXA False False False False False False
2 HBXX False False False False False False
3 HBXX False False False False False False
4 HBXX False False False False False False
Var1_HAYT Var1_HAZD Var1_HBXA Var1_HBXB Var1_HBXC Var1_HBXD \
0 False False False False False False
1 False False True False False False
2 False False False False False False
3 False False False False False False
4 False False False False False False
Var1_HBXH Var1_HBXX Var1_HCXD Var1_HCXF Var1_HCXG Var1_HCYS Var1_HVYS
0 False True False False False False False
1 False False False False False False False
2 False True False False False False False
3 False True False False False False False
4 False True False False False False False (3)计数编码
计数编码为每个类别分配一个数字,该数字表示该类别在数据集中出现的次数。
# 计数编码
count_encoding = data['Var1'].value_counts()
# 为Var1创建一个计数编码的新列
data['Var1_count_encoded'] = data['Var1'].map(count_encoding)
# 显示结果
print(data[['Var1', 'Var1_count_encoded']].head())
输出结果为:
Var1 Var1_count_encoded
0 HBXX 59294
1 HBXA 2123
2 HBXX 59294
3 HBXX 59294
4 HBXX 59294(6)哈希编码
(7)嵌入编码
三、特征工程——特征构造
四、特征工程——特征提取
1、PCA示例
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
pca.fit(X)
print(X)
print(pca.components_)
print(pca.explained_variance_ratio_)
print(pca.singular_values_)
# 创建散点图
plt.scatter(X[:, 0], X[:, 1], color='blue', marker='o')
# 设置标题和标签
plt.title("Scatter Plot of X")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
# 显示图像
plt.grid(True)
plt.show()
输出结果为:

2、IPCA
from sklearn.datasets import load_digits
from sklearn.decomposition import IncrementalPCA
from scipy import sparse
X, _ = load_digits(return_X_y=True)
transformer = IncrementalPCA(n_components=7, batch_size=200)
# either partially fit on smaller batches of data
transformer.partial_fit(X[:100, :])
# or let the fit function itself divide the data into batches
X_sparse = sparse.csr_matrix(X)
X_transformed = transformer.fit_transform(X_sparse)
print(X.shape)
print(X_transformed.shape)输出结果为:
(1797, 64)
(1797, 7)3、KPCA
from sklearn.datasets import load_digits
from sklearn.decomposition import KernelPCA
X, _ = load_digits(return_X_y=True)
transformer = KernelPCA(n_components=7, kernel='linear')
X_transformed = transformer.fit_transform(X)
print(X.shape)
print(X_transformed.shape)输出结果为:
(1797, 64)
(1797, 7)五、特征工程——特征选择
1、手工选择
2、随机特征选择
3、基于统计量的过滤式选择
(1)基于信息增益
(2)基于卡方检验
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.datasets import load_digits
# 加载数据
X, y = load_digits(return_X_y=True)
# 使用卡方检验选择最重要的5个特征
selector = SelectKBest(score_func=chi2, k=5)
X_new = selector.fit_transform(X, y)
# 查看选择的特征
print(selector.get_support()) # 返回被选择特征的布尔数组
print(selector.scores_) # 各特征的得分输出结果为:
[False False False False False False False False False False False False
False False False False False False False False False False False False
False False False False False False False False False True True False
False False False False False False True True False False False False
False False False False False False True False False False False False
False False False False]
[ nan 811.90700411 3501.28249552 698.9252572 438.52969882
3879.81925999 3969.45823205 1193.5608181 24.79521396 2953.83108764
2583.65198939 388.24205944 824.69094853 3676.48924765 1983.5796061
597.24198237 8.95886124 1924.21690377 2409.27140681 3556.31594594
4871.94194551 4782.19921618 2155.17378998 376.76583333 7.90090158
2471.82418401 4515.48149826 2986.64314847 3724.09567634 3208.64686641
5138.07412439 35.71270718 nan 5688.25079535 5262.46646904
3165.0605867 3231.63943369 2532.99695611 3288.81403655 nan
142.85082873 3863.85787901 6416.0867248 5448.25154235 4079.73153383
2134.02540236 4486.34097862 313.53898127 70.39927392 449.72327313
2801.97224468 1527.54519627 1653.15892311 3073.99803898 5251.21748723
683.88227339 9.15254237 851.06791492 3800.2473108 730.92975659
1859.53966338 4379.2250408 5059.00551511 2281.32864013](3)基于互信息
六、附录
1、计算类别型特征之间的相关性的方法:Cramér’s V
Cramér's V 是一种用于衡量两个类别型变量之间相关性的方法。它用于检验和量化两个分类变量之间的关联强度。Cramér's V 的值范围在 [0, 1] 之间,其中:
- 0 表示完全没有关联(两个变量完全独立)。
- 1 表示两个变量完全相关。
它常用于分析两个分类变量之间的关系,尤其是当数据是类别型(名义数据)时,Cramér's V 是一个非常有用的工具。
(1)Cramér's V 计算方法
Cramér's V 是基于 卡方检验(Chi-squared test) 的结果进行计算的。计算的公式为:
其中:
是卡方统计量。
- n 是样本的总数。
- k 是第一个变量的类别数(特征的种类数)。
- r 是第二个变量的类别数。
步骤:
- 构造列联表(Contingency Table):列联表是描述两个分类变量之间关系的二维表格,表格中的每个单元格表示某一类别组合的频数。
- 计算卡方统计量:基于列联表计算卡方统计量,卡方统计量衡量观察到的频数与期望频数之间的差异。
- 计算 Cramér's V:使用上述公式来计算 Cramér's V 值,得出变量之间的相关性。
(2)Cramér's V 的应用场景
- 探索数据:通过计算 Cramér's V,可以帮助我们理解分类变量之间的关系,这对于后续的特征工程和模型构建有很大的帮助。
- 变量选择:在多种特征选择方法中,Cramér's V 可用于筛选那些与目标变量相关性较大的特征,去除不相关的特征。
(3)Cramér's V 的优缺点
优点:
- 适用性广泛:Cramér's V 可以应用于任何类别型变量(即使是多类别变量),它是一个通用的关联性度量。
- 直观易懂:它的值范围明确且容易理解,0 表示无关联,1 表示完全相关。
缺点:
- 对大样本敏感:卡方统计量和 Cramér's V 对样本大小敏感。在大样本的情况下,Cramér's V 可能高估变量之间的关系,因此需要结合实际应用进行判断。
- 不考虑顺序信息:Cramér's V 不适用于顺序型变量(即顺序的类别数据)。如果数据有顺序(例如:小、中、大),则需要使用其他方法(如 Kendall's Tau 或 Spearman's ρ)。
(4)Cramér's V 的计算步骤
假设我们有一个数据集,其中 var1 和 var2 是两个类别型特征,下面是如何计算它们之间的 Cramér's V 的步骤:
步骤 1:构造列联表(Contingency Table)
构造一个列联表来表示 var1 和 var2 两个特征的频次分布。
步骤 2:计算卡方统计量
使用卡方检验来计算列联表的卡方统计量:
其中:
- O 是观察到的频数。
- E 是期望的频数,期望频数的计算方法是:
步骤 3:计算 Cramér's V
根据卡方统计量、样本总数以及列联表的大小计算 Cramér's V。
(5)Python 中计算 Cramér's V
在 Python 中,可以使用 association-metrics 库或手动实现计算 Cramér's V。
手动计算 Cramér's V:
import numpy as np
import pandas as pd
from scipy.stats import chi2_contingency
def cramers_v(x, y):
# 创建列联表
contingency_table = pd.crosstab(x, y)
# 计算卡方统计量
chi2, p, dof, expected = chi2_contingency(contingency_table)
# 计算Cramér's V
n = contingency_table.sum().sum()
min_dim = min(contingency_table.shape) - 1
cramers_v_value = np.sqrt(chi2 / (n * min_dim))
return cramers_v_value
# 示例数据
data = {'var1': ['A', 'B', 'A', 'C', 'B', 'A'],
'var2': ['X', 'Y', 'X', 'Y', 'X', 'Z']}
df = pd.DataFrame(data)
# 计算 Cramér's V
cramers_v_value = cramers_v(df['var1'], df['var2'])
print(f"Cramér's V: {cramers_v_value}")
(5)如何解释 Cramér's V
- 0:完全没有关联(变量之间独立)。
- 0 < V < 0.1:变量之间几乎没有关联,可能没有显著关系。
- 0.1 ≤ V < 0.3:较弱的关联。
- 0.3 ≤ V < 0.5:中等程度的关联。
- 0.5 ≤ V < 0.7:强关联。
- V ≥ 0.7:非常强的关联,表示变量之间有很强的相关性。
总结
Cramér's V 是一种衡量两个类别型变量之间相关性的统计量。它结合了卡方检验的思想,能够定量描述变量之间的关联强度。通过计算 Cramér's V,我们可以评估特征间的关系,帮助我们进行特征选择、数据探索和建模。
2、计算数值型特征与类别型特征之间相关性的方法:Eta^2 (Correlation Ratio) 相关比
Eta²(Eta squared),也称为 相关比(Correlation Ratio),是一种用于衡量数值型特征与类别型特征之间关联性的统计量。Eta² 衡量的是类别型自变量对数值型因变量的变异贡献,它在分析不同组别之间的差异时非常有用。
Eta² 可以看作是 变异度 的度量,它表示因变量的总变异中有多少比例是由类别变量的不同水平引起的。它常用于 单因素方差分析(ANOVA) 中来评估自变量(分类变量)对因变量(数值变量)的影响。
(1)Eta² (Correlation Ratio) 计算原理
Eta² 是通过以下公式计算的:
其中:
:组间平方和(Between-group sum of squares),表示由类别型特征(自变量)的不同水平所导致的因变量的变异。
:总平方和(Total sum of squares),表示因变量的总变异。
具体地,Eta² 衡量的是类别型特征引起的变异占因变量总变异的比例。Eta² 的值范围在 [0, 1] 之间:
- 0 表示类别型特征对数值型特征没有解释力(即不相关)。
- 1 表示类别型特征完全解释了数值型特征的变异。
(2)Eta² 计算步骤
步骤 1:计算总变异(Total Sum of Squares, )
)
总变异是指数值型变量相对于其均值的偏差的平方和:
其中 yiy_iyi 是第 iii 个样本的数值,yˉ\bar{y}yˉ 是数值型特征的均值。
步骤 2:计算组间变异(Between-group Sum of Squares, )
)
组间变异表示的是各个类别的均值相对于总均值的偏差的平方和,计算公式为:
其中:
是类别的数量。
是每个类别中的样本数量。
是第 j 类别的均值。
步骤 3:计算 Eta²
最后,使用上述公式计算 Eta²:
(3)Eta² 的应用场景
- 分析类别型特征对数值型特征的影响:Eta² 适用于评估分类变量与连续变量之间的关系,尤其在分析每个类别的均值是否与其他类别有显著差异时使用。
- ANOVA 中的检验:Eta² 是 ANOVA(方差分析)中常见的效果大小指标。通过 ANOVA,我们可以检验类别型变量对因变量的影响是否显著,并通过 Eta² 来衡量这个影响的大小。
- 特征选择:Eta² 可以用于特征选择,尤其是当数据中包含类别型特征时,可以评估哪些类别型特征对目标变量的贡献较大。
(4)Eta² 的解释
Eta² 的值范围为 0 到 1,解释如下:
- 0:类别型特征与数值型特征之间没有关系,类别型特征没有解释数值型特征的变异。
- 0.01 - 0.06:较小的效应,类别型特征对数值型特征的影响较小。
- 0.06 - 0.14:中等效应,类别型特征对数值型特征有一定的影响。
- 0.14 - 0.30:较大的效应,类别型特征对数值型特征有较大影响。
- >0.30:非常大的效应,类别型特征对数值型特征的影响非常显著。
(5)Python 中计算 Eta²
在 Python 中,我们可以使用 scipy.stats.f_oneway 或 statsmodels 来进行方差分析,并计算 Eta²。以下是使用 ANOVA 和手动计算 Eta² 的示例代码。
import numpy as np
import pandas as pd
from scipy import stats
# 假设我们有一个数据集,其中 'Category' 是类别型特征,'Value' 是数值型特征
data = {'Category': ['A', 'A', 'B', 'B', 'C', 'C'],
'Value': [10, 12, 25, 30, 15, 18]}
df = pd.DataFrame(data)
# 使用 ANOVA 来进行方差分析
categories = [df[df['Category'] == category]['Value'] for category in df['Category'].unique()]
f_statistic, p_value = stats.f_oneway(*categories)
# 计算 Eta²
# 计算组间变异 (SS_between)
mean_total = df['Value'].mean() # 总均值
ss_total = np.sum((df['Value'] - mean_total) ** 2) # 总平方和
ss_between = np.sum([len(group) * (group.mean() - mean_total) ** 2 for group in categories]) # 组间平方和
# 计算 Eta²
eta_squared = ss_between / ss_total
print(f"F-statistic: {f_statistic}")
print(f"P-value: {p_value}")
print(f"Eta²: {eta_squared}")
(6)解释代码中的 Eta² 计算
- 创建数据:我们创建一个包含类别型特征
'Category'和数值型特征'Value'的 DataFrame。 - 方差分析(ANOVA):使用
scipy.stats.f_oneway对每个类别进行单因素方差分析,检验类别型特征与数值型特征之间是否存在显著差异。 - 计算 Eta²:
- 计算总平方和
。
- 计算组间平方和
。
- 使用公式计算 Eta²。
- 计算总平方和
(7)总结
Eta²(相关比) 是衡量类别型特征与数值型特征之间关联性的重要统计量。它是 ANOVA 中的一个关键效果大小指标,能够告诉我们类别型特征对于数值型特征变异的解释程度。通过计算 Eta²,我们可以了解某个分类变量对数值型目标变量的影响程度,从而帮助我们在特征选择、数据探索以及模型解释中做出更好的决策。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








