Dijkstra/Floyd

最新推荐文章于 2025-03-29 20:48:01 发布

晴天的鱼

最新推荐文章于 2025-03-29 20:48:01 发布

阅读量426

点赞数 1

文章标签： dijkstra 算法

本文链接：https://blog.youkuaiyun.com/m0_56422883/article/details/118303939

版权

Dijkstra

什么是Dijkstra

dijkstra是一种单源最短路径算法,时间复杂度上限为O(n^2)在实际应用中较为稳定;;加上堆优化之后更是具有O((n+m)log2n)的时间复杂度,在稠密图中有不俗的表现。

Dijkstra的原理

dijkstra本质上的思想是贪心,它只适用于不含负权边的图。

Dijkstra流程

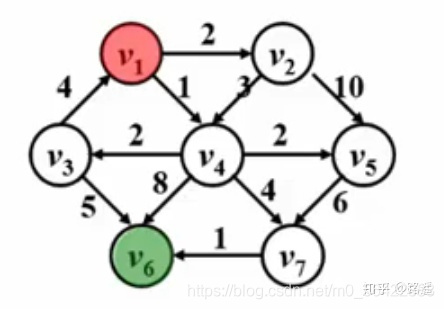
一，把图中所有顶点分成两组，第一组S:已确定最短路径的终点集合(初始只含源点v1)，第二组V-S:尚未确定最短路径的顶点结合(初始V-{v1})。
二，按最短路径长度递增的顺序逐个把V-S的顶点加到第一组法，直至从v1出发可以到达的所有顶点都包括到第一组中。
三。在这过程中，总保持从V,到S各顶点的最短路径长度都不大于从V1到V-S的任何顶点的最短路径长度。

代码实现

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;

int N,M,S;//N为图的点数，M为图的边数，S为源点
int GWeight[502][502];//用二维数组储存图的边的权重
int path[505],collected[505] = {0},dist[505];
/**********************************************************************
 * path数组用来储存S到结点V的最短路径的V的前一个结点W，即path[V] = W  *
 * 例：路径S->A->B->W->V是S到V的最短路径，那么path[V] = W             *
 * collected是bool数组结点是不是在集合里                              *
 * dist是从S为起始点到结点V的最短路径长度，如上例，dist[V] = 4        *
 **********************************************************************/
const int INF = 0x3f3f3f;//假设所有边的权重不超过INF，INF为无限大

void init()//在读入数据之前初始化图
{//GWeight和dist在读取数据之前都初始化为INF，path初始化为-1
    for(int i = 0; i < 502; i++){
        path[i] = -1;
        dist[i] = INF;
        for(int j = 0; j < 502; j++){
            GWeight[j][i] = INF;
        }
    }
    memset(collected,0,sizeof(collected));//起初，集合里没有任何元素
}

int FindMin()//在不在集合里的结点 且 与集合内结点有边的结点里 找结点的dist的最小值
{
    int minV = 0;
    int minDist = INF;
    for(int i = 0; i < N; i++){
        if(!collected[i] && dist[i] < minDist){
            minV = i;
            minDist = dist[i];
        }
    }
    return minV;
}

void Dijkstra()
{
    dist[S] = 0;//源点的距离设为0
    collected[S] = true;//将源点放入集合
    for(int i = 0; i < N; i++){//更新S周围结点的dist值，与此同时其它结点的dis = INF
        dist[i] = GWeight[i][S];
        if(dist[i] < INF)
            path[i] = S;
        else
            path[i] = -1;
    }

    while(1){
        int v = FindMin();
        if(!v)//集合以外没有结点了
            return;
        collected[v] = true;//将该节点加入集合
        for(int i = 0; i < N; i++){//新结点加入集合会影响其它不在集合里dist的最小值
            if(!collected[i]){
                if(dist[v] + GWeight[v][i] < dist[i]){
                    dist[i] = dist[v] + GWeight[i][v];
                    path[i] = v;
                }
            }
        }
    }
}

Dijkstra优化

遇到比较大的数据（例如n≤100000）就完美地炸掉了，所以我们要找一个东西来优化它。这个东西就是优先队列：priority queue！这个东西使用堆，只用O(log n)的时间复杂度就可以将n个元素在一个队列中排好序，其操作和普通队列相似。

什么是堆

堆就是一个要求每个节点的父亲节点优先级比该节点高的二叉树，插入一个元素时把它放到最低点，如果比父亲节点优先级高就与父亲节点交换，直到满足上述条件为止。

存储数据

用堆对Dijkstra优化时需要定义一个结构体来存节点和距离，但是我们不能直接把它放进堆，原因很简单，它不知道你要比较什么，就像sort比较结构体一样，不过优先队列的处理方式和sort不同，需要重载运算符。

struct stru{//定义结构体
  int num,dis;
  bool operator ()(stru a,stru b){//重载运算符
    return a.dis > b.dis;
  }
};

如何松弛

这还没完，因为这些数据刚放进去就跑得无影无踪，我们在松弛的时候总不能把堆内元素全导出来再导回去，那样时间复杂度就又成O(n²)了。其实我们只需要在取堆顶的时候判断一下这个点是不是已经取过就可以了。

参考代码

struct edge {
	int to, dis, next;
};
edge e[MaxM];
int head[MaxN], dis[MaxN], cnt;
bool vis[MaxN];
inline void add_edge( int u, int v, int d ) {
	cnt++;
	e[cnt].dis = d;
	e[cnt].to = v;
	e[cnt].next = head[u];
	head[u] = cnt;
}
struct node {
	int dis;
	int pos;
	bool operator <( const node &x )const {
		return x.dis < dis;
	}
};
std::priority_queue<node> q;
inline void dijkstra() {
	dis[s] = 0;
	q.push( ( node ) {
		0, s
	} );
	while( !q.empty() ) {
		node tmp = q.top();
		q.pop();
		int x = tmp.pos, d = tmp.dis;
		if( vis[x] )
			continue;
		vis[x] = 1;
		for( int i = head[x]; i; i = e[i].next ) {
			int y = e[i].to;
			if( dis[y] > dis[x] + e[i].dis ) {
				dis[y] = dis[x] + e[i].dis;
				if( !vis[y] ) {
					q.push( ( node ) {
						dis[y], y
					} );
				}
			}
		}
	}
}

Floyd

什么是floyd

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法。

算法思想

适用范围

任意两点间的最短路径。

缺点

时间复杂度:是O(n^3)，不适合计算大量数据。

代码实现

for(int k=1;k<=n;k++){
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);