第8章 代数系统

2024年12月26日

2025年1月1日（🌷）

🐇8.1 二元运算及其性质🥕

        一个  抽象代数系统  有三方面的要素：集合、集合上的运算以及说明运算性质或运算之间关系的公理。为了研究抽象的代数系统，需要先定义代数运算以及运算的性质，并通过选择不同的运算性质来规定各种抽象代数系统的定义。在此基础上再深入研究这些抽象代数系统的内在特性和应用。
        抽象的代数系统也是一种数学模型，可以用它表示实际世界中的离散结构。抽象代数在计算机中有着广泛的应用，例如自动机理论、编码理论、形式语义学、代数规范、密码学等都要用到抽象代数的知识。

🐄🐾8.1.1 定义和表示🥛

定义在 集合上面 的运算

🥒🥗二元运算🍓

🥒🥗一元运算🍓

🐄8.1.2 二元运算的性质

🐇8.2 代数系统🥕

🐄8.2.1 定义和实例

🐄8.2.2 子代数系统

🐄8.2.3 代数系统的同态与同构

🐇8.3 半群与独异点🥕

🐄8.3.1 定义与性质

🐄8.3.2 子系统与直积

🐇8.4 群🥕

🐄8.4.1 群的定义

🐄8.4.2 群的性质

🐄8.4.3 子群的定义

🐄8.4.4 特殊的群

🐄8.4.5 陪集与拉格朗日定理

🐄8.4.6 正规子群与商群

🐄8.4.7 群的同态与同构实例

🐇8.5 环与域🥕

🐄8.5.1 环

🐄8.5.2 域

🐇8.6 格与布尔代数🥕

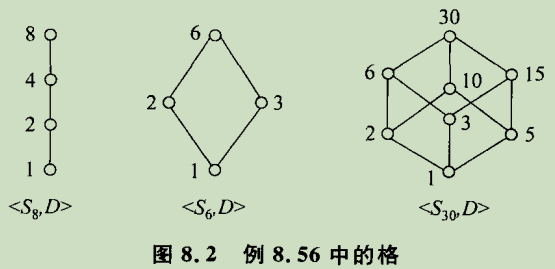
🐄8.6.1 格

我人过来了，我格丢那了

🐄8.6.2 布尔代数

🐇8.7 组合电路🥕