文章讲述了在数学计算中如何运用构造函数技巧定义导数，涉及等价无穷小概念，以及在处理极限问题时如何通过举例和替换进行求解，强调了洛必达法则和泰勒展开法的重要性，提醒读者注意自变量和变量的区别，以及避免中值定理带来的误导。
《1800》
1
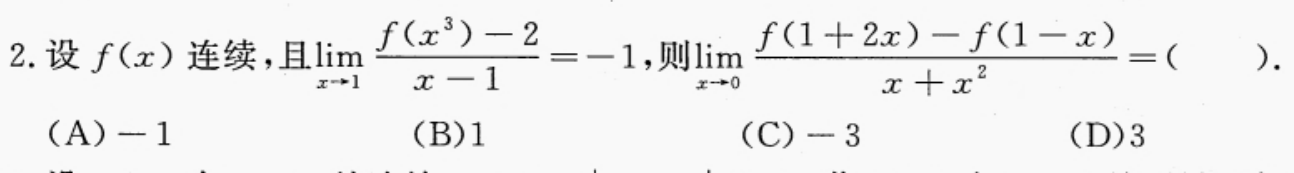
缺乏构造函数的技巧
2
3
等价无穷小+构造函数
4
这个构造有点难。补充几个数字构造导数定义
5
6
通过举例子排除真的好
7
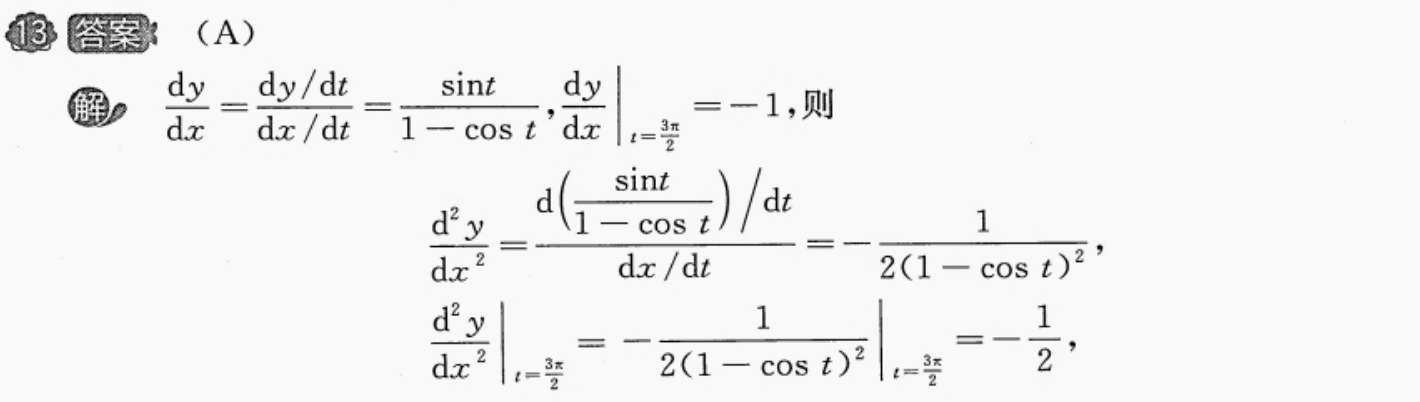
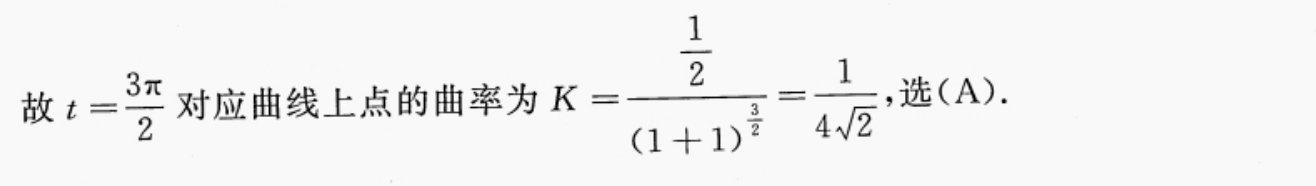
8
我不想输
9
注意自变量为x的平方
10
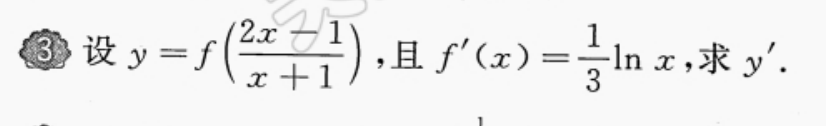
导数对应的x为y的变量
11
代入定义式
12
《三大计算》
13
14
这个替换妙呀
15
16
注意：h为变量
17
终于自己写出来了
18
19
20
21
22
23
救命，还是要分开
24
计算失误
25
26
27
28
29
30
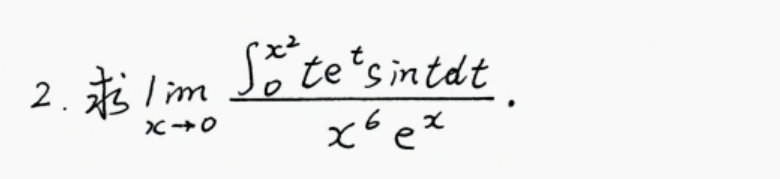
31
把上面的换下，就可以施行洛必达法则
32
33
34
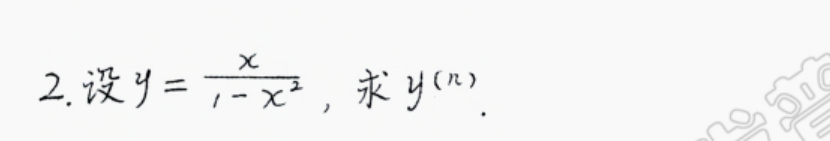
李正元
35
36
37
38
39
41
注意最后自变量是y
42
43
44
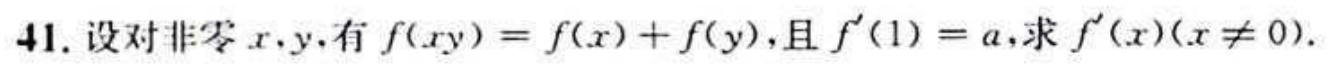
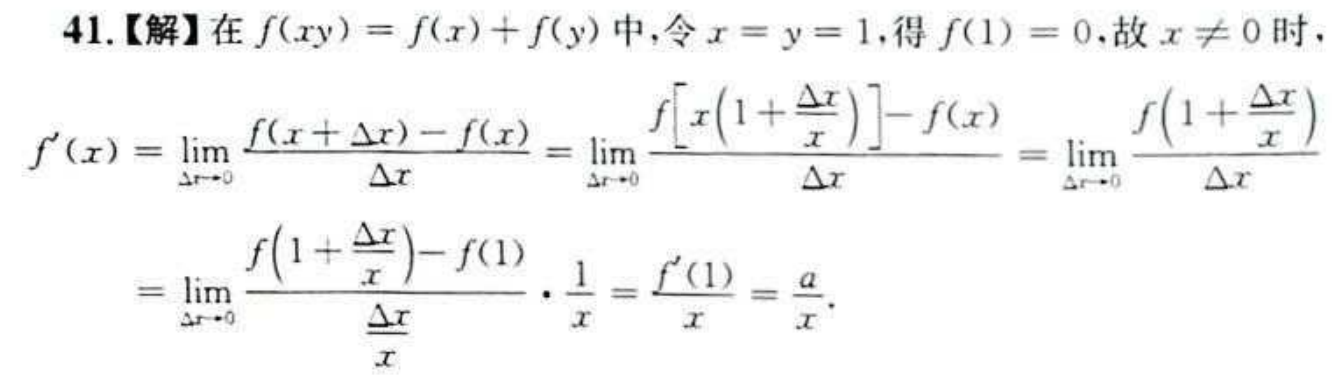
45
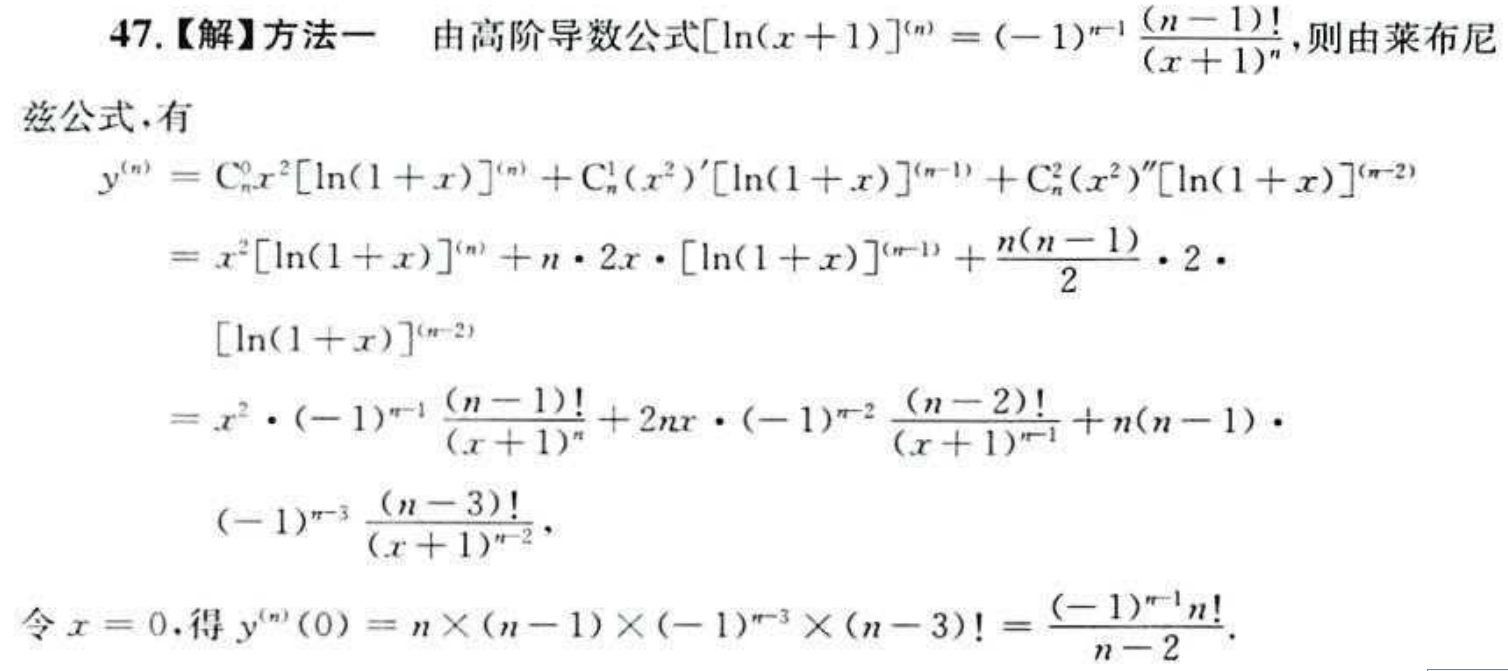
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
1+sinx这一步为什么永远写不出来
67
68
69
70
71
72
73
74
75
76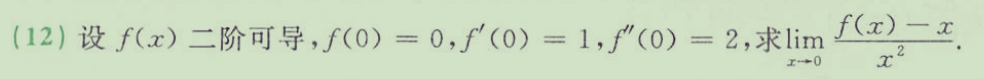
77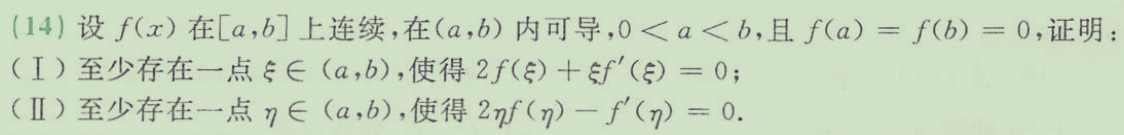
78
79
80
81
82
83
84
85
86
87
88
应该想到用泰勒展开的
89
90
91
92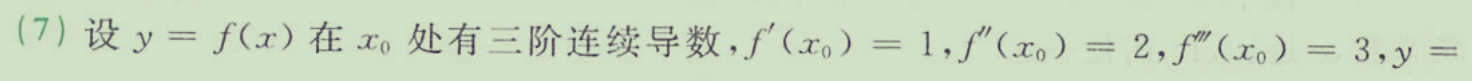
93
直接用原函数
94
95
96
97
最后不能想当然地带进去，要构造定义进行计算
98
99
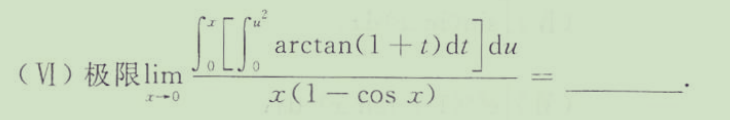
100
101
102
103
104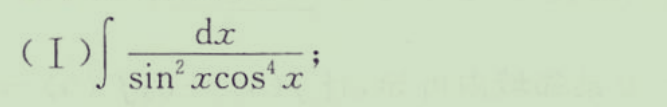
105
106
107
108
109
可恶的中值定理
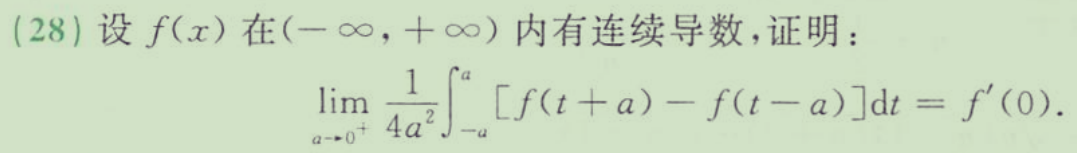
113
114
116
119
120
扫一扫
1644
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
