数据结构（五）树与二叉树

快乐做自己

已于 2024-12-12 20:16:02 修改

阅读量3.1k

点赞数 3

文章标签：笔记

于 2024-05-26 17:03:04 首次发布

本文链接：https://blog.youkuaiyun.com/m0_56366826/article/details/139216177

版权

2024年5月26日一稿（王道P142）

2024年9月14日

2024年9月30日

2024年10月20日

2024年10月29日

2024年11月6日

2024年11月8日

2024年11月10日

2024年11月11日（杀出一条血路）

2024年11月13日（希望）

2024年11月18日（彩云）

19（绝不会把自己的人生完蛋）

-9的原码

树的计算-哔哩哔哩_bilibili

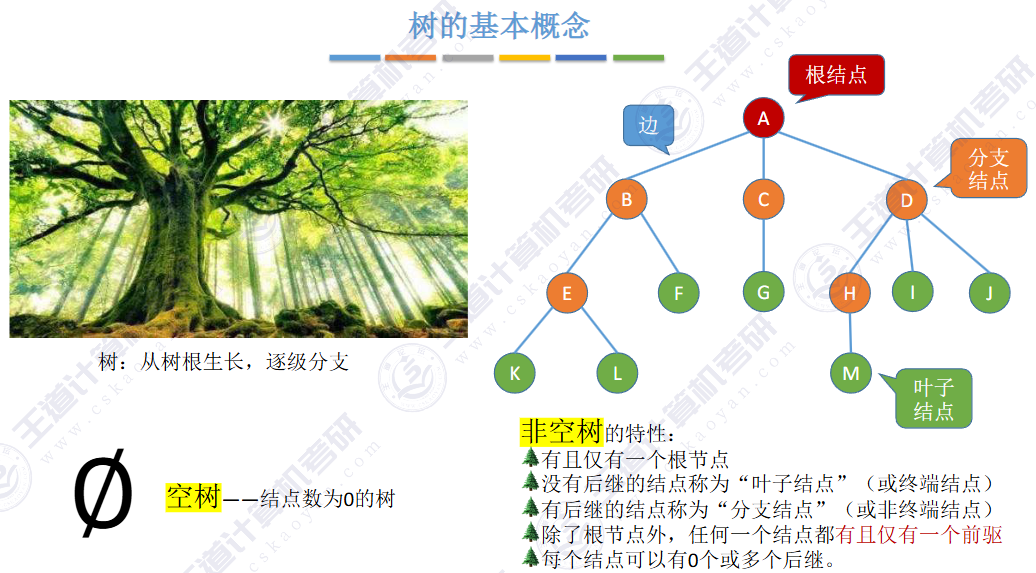
👉树型结构👈是一类重要的✍非线性数据结构

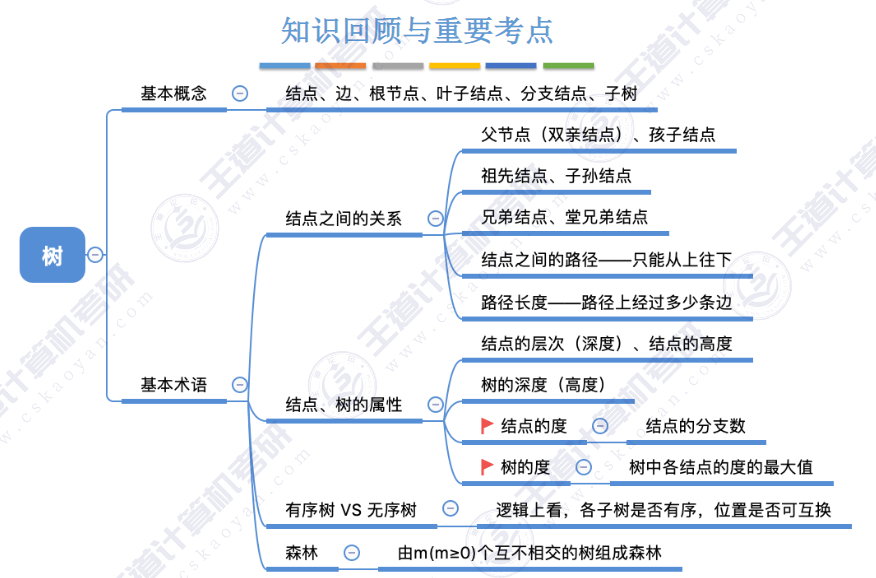
🏀基本概念🍁

▶ 子树是不相交的

▶ 除了根节点外，每个节点有且仅有一个父节点

▶ 一棵 N 个节点的树有 N-1 条边

结点数为0的树又称之为空树

🚢术语

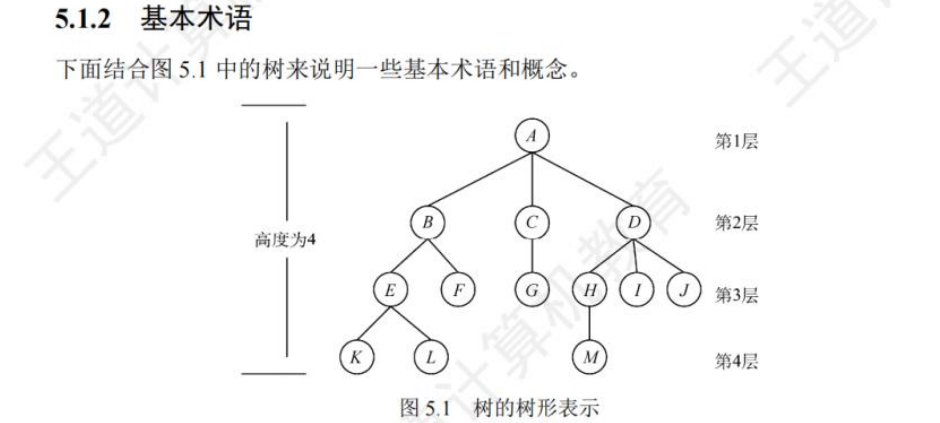
🚢性质

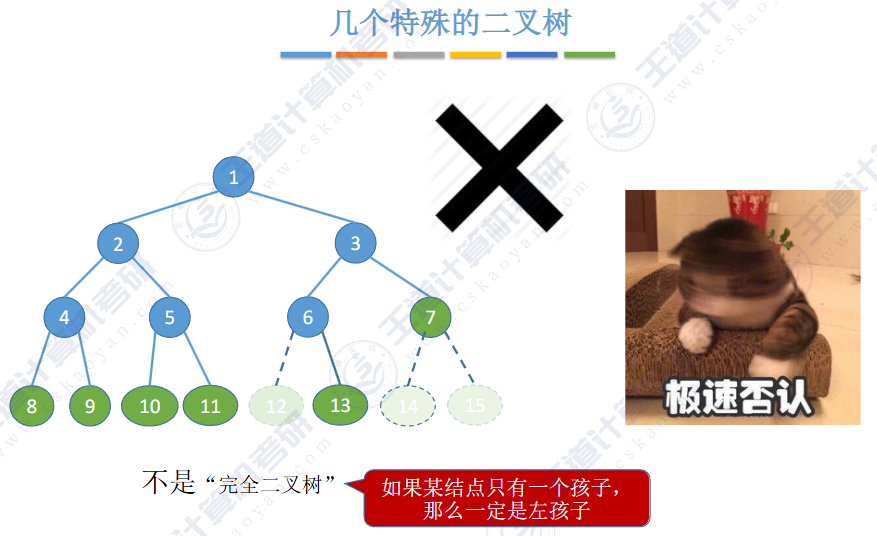
🚀二叉树

注意：层也可以为0

【【考研408 数据结构】叶节点怎么数 | 完全二叉树重点题型(上)】 https://www.bilibili.com/video/BV1VH4y1d7K7/?share_source=copy_web&vd_source=0caeacd6c3217ba41c56ea47a129e168

【【考研408 数据结构】画汉堡秒杀! | 完全二叉树重点题型(下)】 https://www.bilibili.com/video/BV1ku4y1p7Ky/?share_source=copy_web&vd_source=0caeacd6c3217ba41c56ea47a129e168

🚢性质

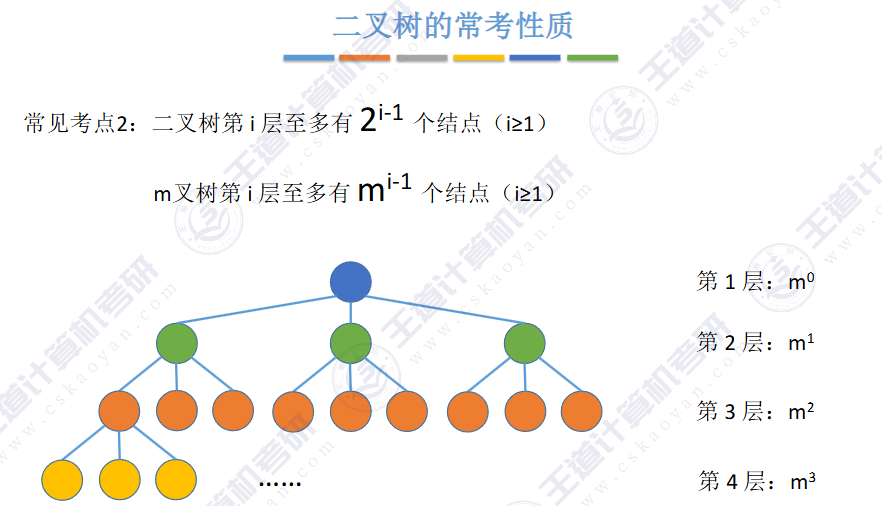
或者由二叉树 N0 = N2 + 1

🥎5.2.2 二叉树存储结构🍁

🚢顺序存储

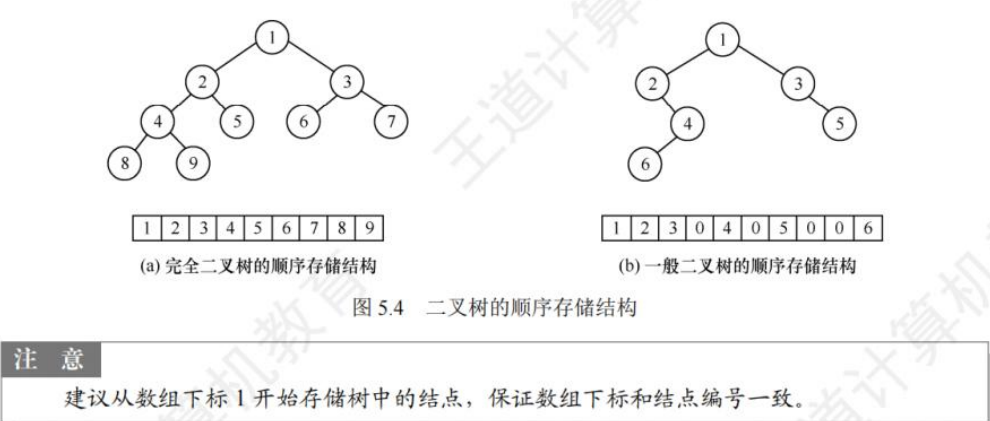
🚢2022年真题

序号之前的是分支节点之后的是叶子节点
二叉树，左孩子：2i + 1;右孩子：2i+2。根据数组对应下标

中序遍历是有序的

typedef struct{
int SqBiTNode[MAX_SIZE];//保存二叉树结点值的数组
int ElemNum;//实际占用的数组元素个数
}SqBiTree;


// 判断是否为二叉搜索树
bool DFS(SqBitree *T, int i, int & Pre)//T:当前节点，i:在数组中位置，Pre:前驱
{
//边界条件：1：左右子树为空，2：i>数组元素个数.就是前面的都是对的
if(T.SqbiTNode[i] == -1 || i > ElemNum)
{
    return true;
}

利用中序遍历判断是否为 二叉搜索树

/*左边*/
//判断左子树
if(! DFS(T, 2*i + 1， Pre)) return false;

/*中间*/
//判断是否大于根节点
if(T.SqBiTNode[i] <= Pre) return false;
//更新当前节点
Pre = T.SqBiTNode[i];


/*右边*/
//判断右子树
if(! DFS(T, 2*i + 2, Pre)) return falae;

return true;

}

提示

①度为1的二叉树。此时虽然树中结点最多只有一个孩子，但还是要区分这个孩子是左孩子还是右孩子。

②二叉树和度为2的树是不同的：二叉树要求每个结点的度不超过2，但不一定要有度为2的结点。而度是2的树则是每个结点的度不超过2且至少有一个度为2的结点，即二叉树不一定是度为2的树。

③含有n个结点的二叉树最多有 $C_{2n}^{n}/(n+1)=\frac{{(}2n)!}{n!(n+1)!}$ 种形态。

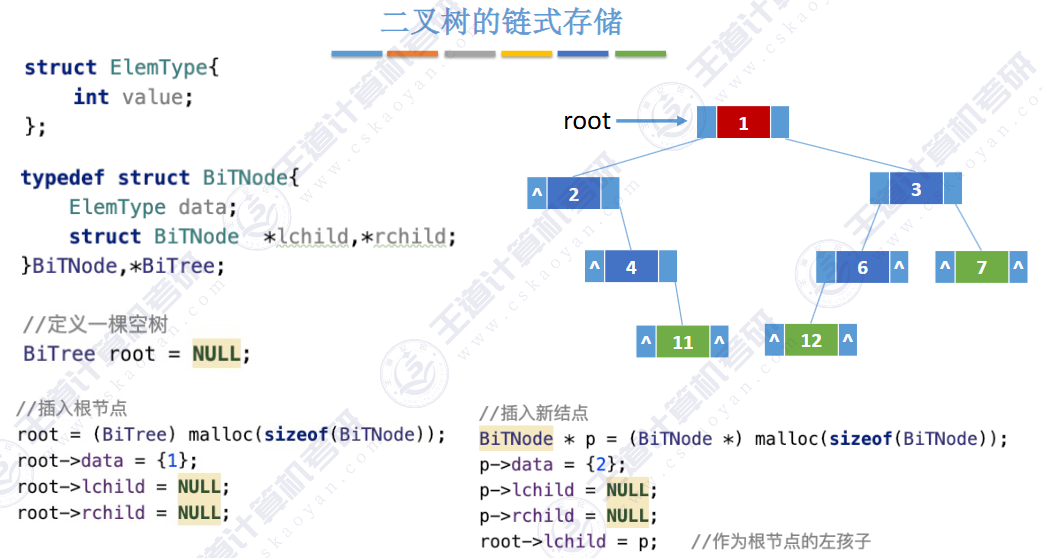
🚢链式存储

提示：还可增加指向父结点的指针，此时则为三叉链表。

🚢双亲表示法

顺序表

方便找到父亲，但是找孩子需要遍历整个顺序表

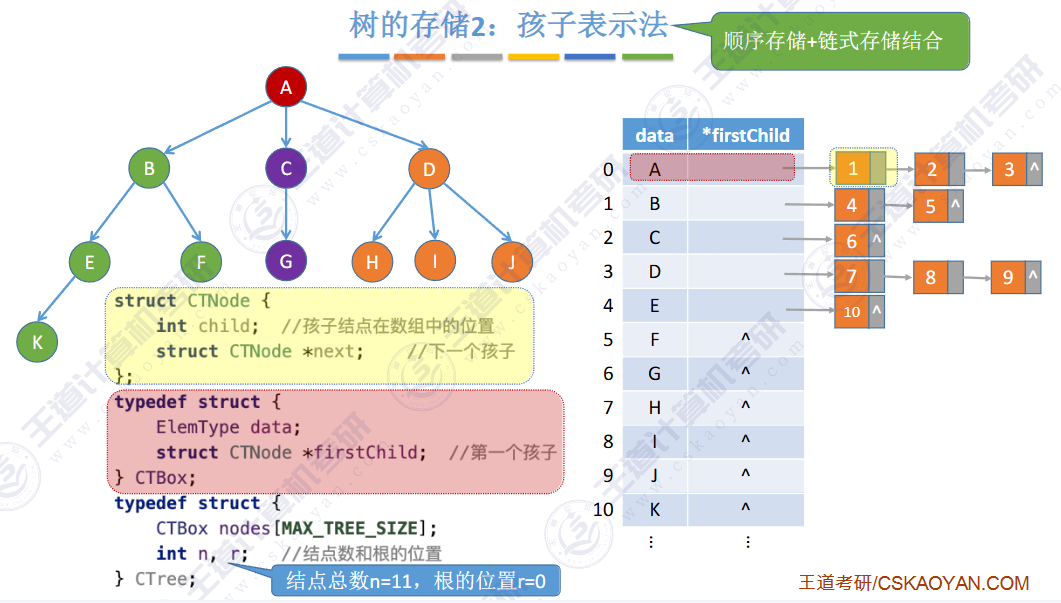
🚢孩子表示法

适合找孩子，不适合找双亲

💦 性质1：树中的节点数等于所有节点度数加 1（n = V + 1）

限制在了7，但是找到第一个0依旧还是可以出第7个空格

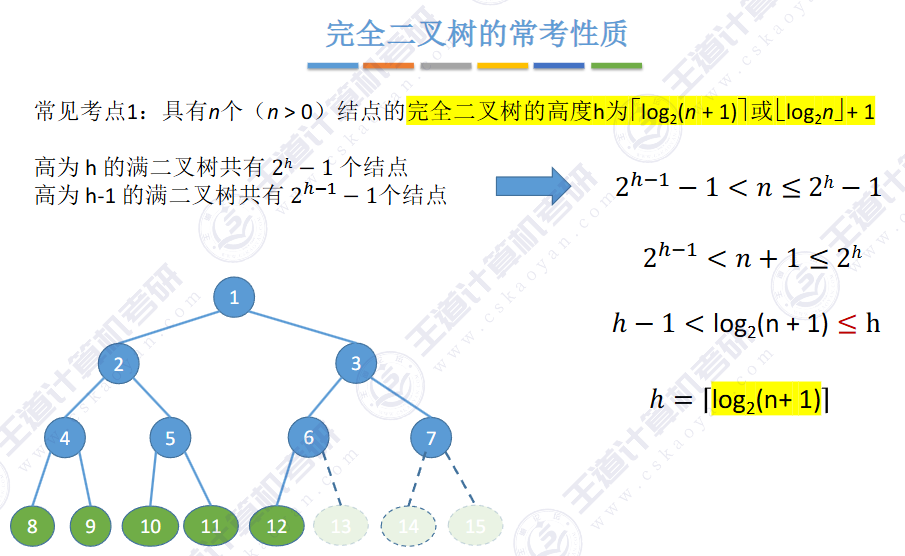
完全二叉树

总结点数为偶数度为1的结点数：1个

奇数 0个

往上挂

顺序<三元组

除了根节点都要存储指向父节点的指针

卡特兰树---->二叉树

只关注形态

需要去除根结点计算

下面这个可以直接卡特兰树

🎱5.3 二叉树的遍历和线索二叉树🍁

🚀5.3.1 二叉树的遍历

由上图得知，普通二叉树也可以使用数组来存储，但是会存在大量的空间浪费，而完全二叉树就不会这样，因为其空间利用率是％100的。既然这样，那普通二叉树该如何进行存储呢？答案是使用链式结构进行存储。

BST（二叉排序树）

🚢先序遍历

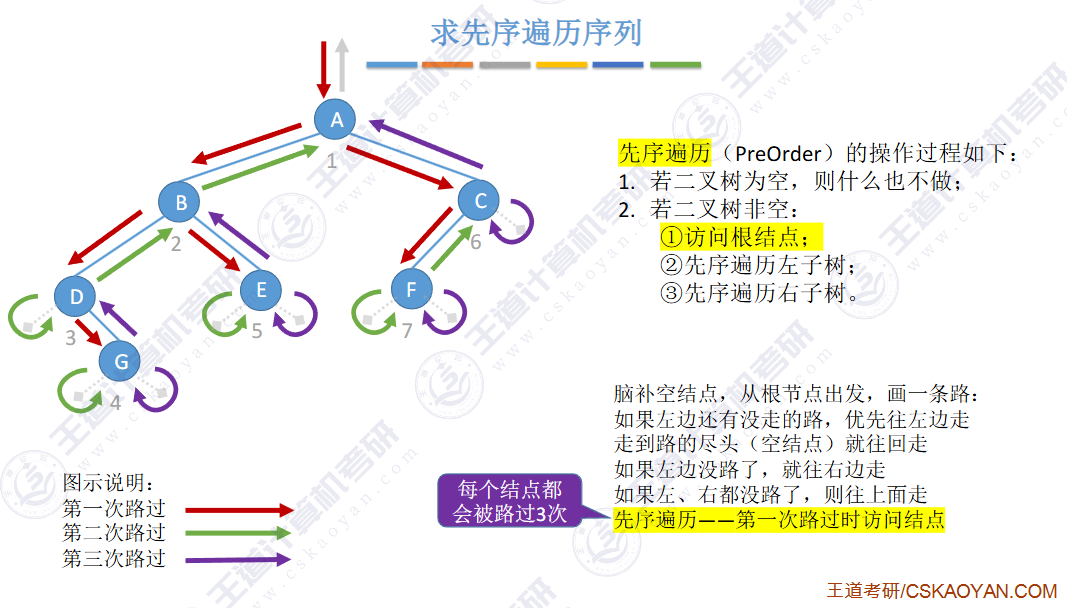
// 前序遍历 根 左 右
void  PrevOrder(BT* root)
{
	if (root == NULL)
	{
		printf("NULL "); // 如果为空，就打印
		return;      // 当前函数结束
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

🚢中序遍历

🚢后序遍历

🚢层次遍历（不用递归，用队列）

🚀二叉排序树

左子树上所有结点的关键字均小于根结点的关键字，右子树上所有结点的关键字均大于根结点的关键字，左子树和右子树又各是一棵二叉排序树。

✨二叉排序树用于元素的搜索和排序。

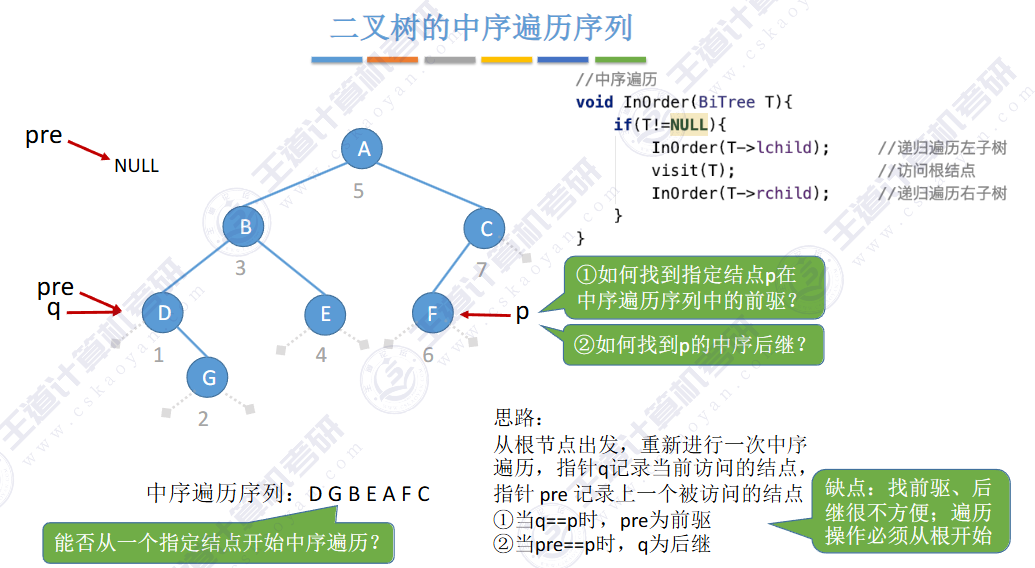
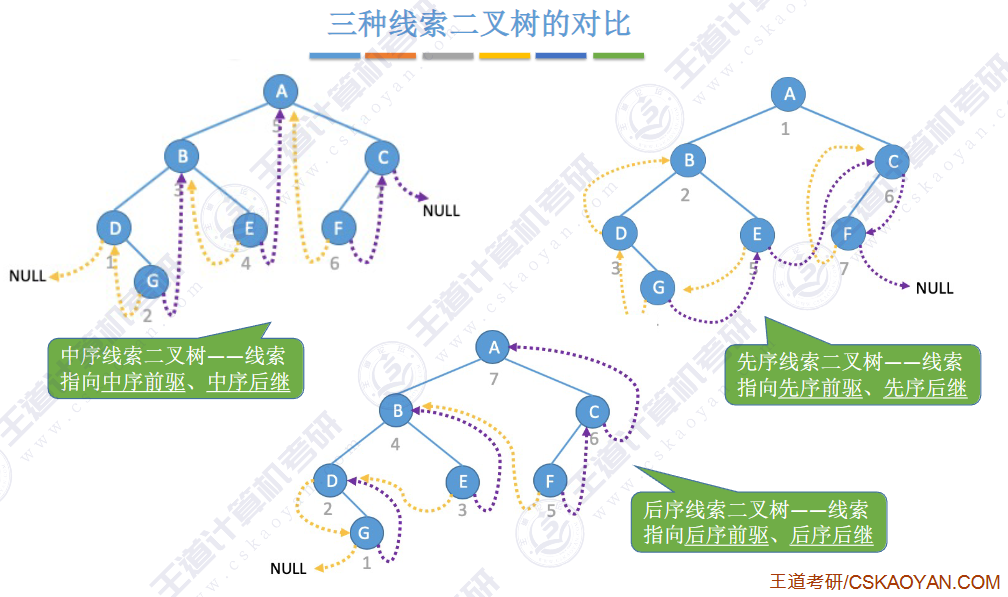
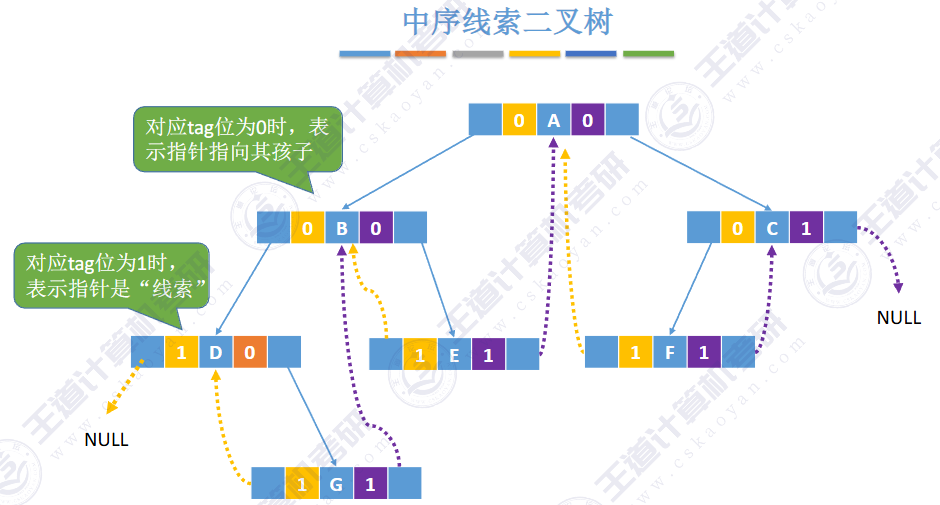
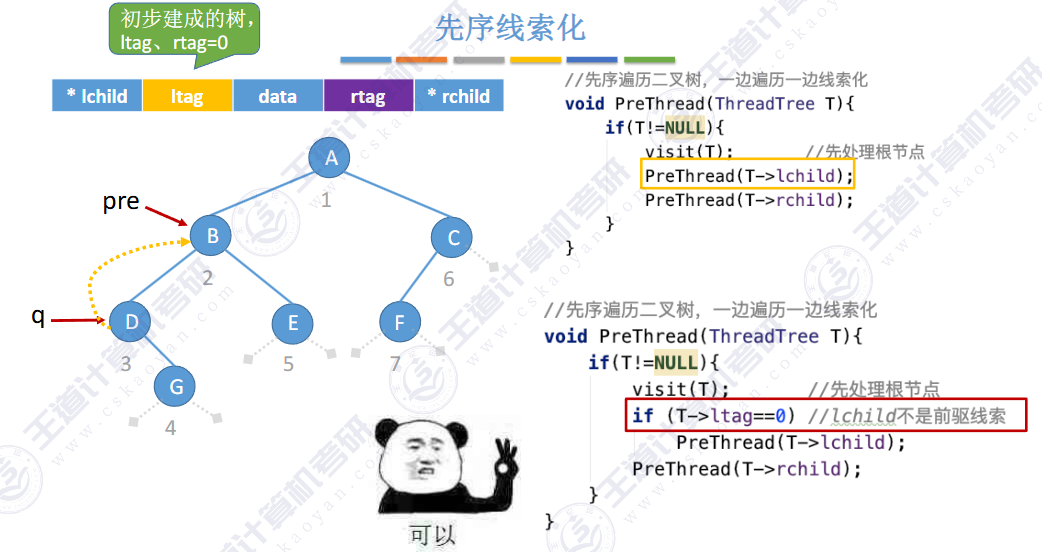
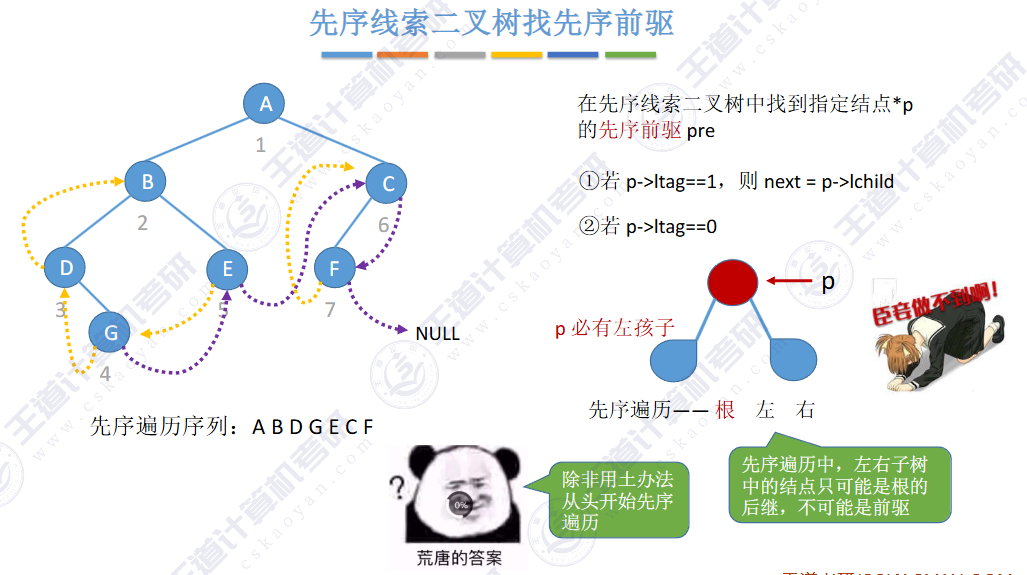
🚀5.3.2 线索二叉树

相对于根节点

指向结点前驱和后继的指针，叫做👉线索👈

【中序线索二叉树】 https://www.bilibili.com/video/BV1Bf4y1G7To/?share_source=copy_web&vd_source=0caeacd6c3217ba41c56ea47a129e168

先叶后根

🏐5.4 树森林🍁

🚀5.4.1 存储结构

【数据结构17-2分钟搞定树的存储结构】 https://www.bilibili.com/video/BV1as4y177wt/?share_source=copy_web&vd_source=0caeacd6c3217ba41c56ea47a129e168

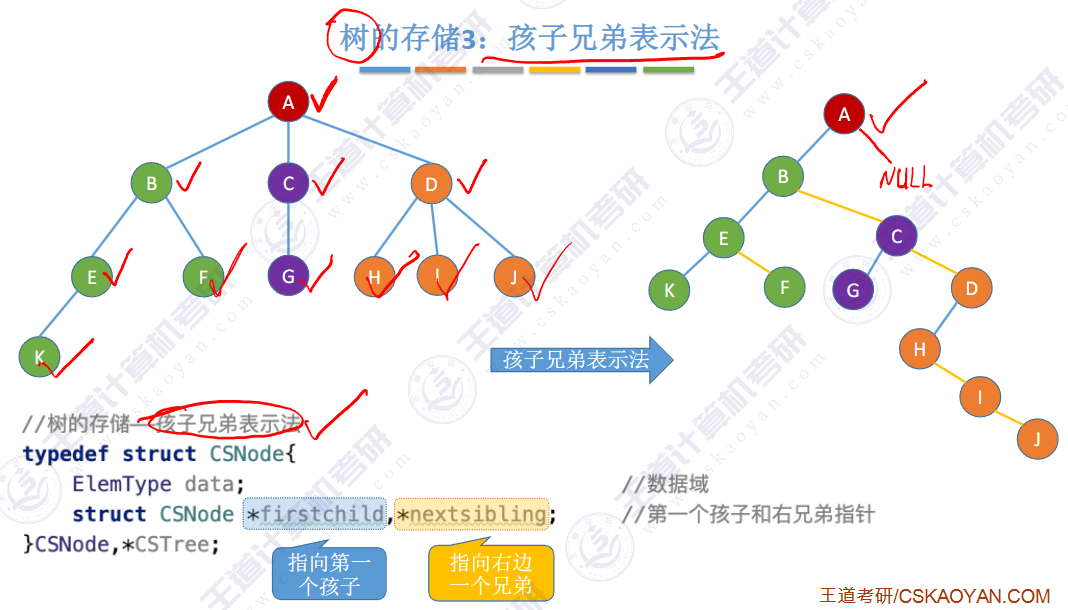
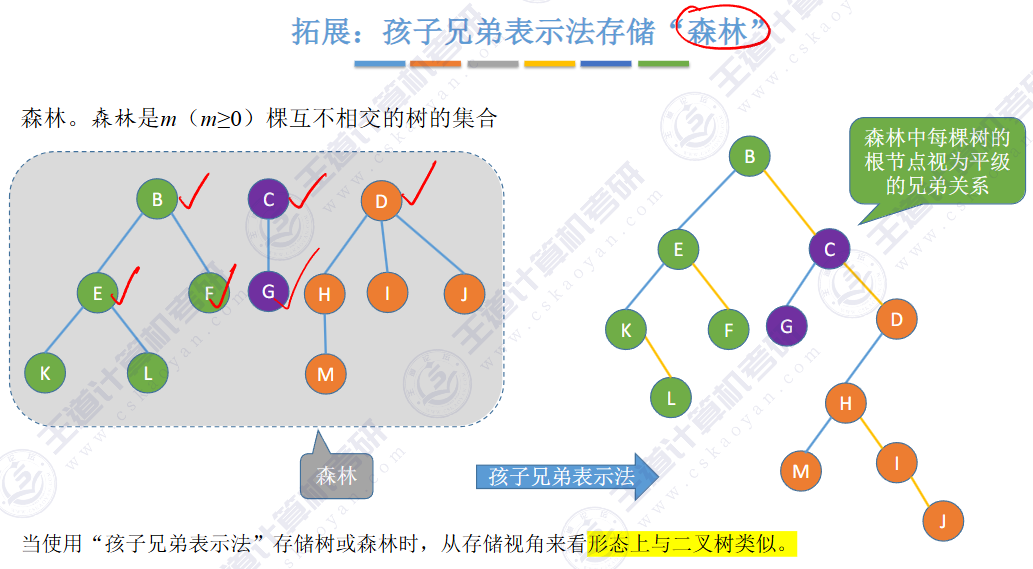
🚀5.4.2 树、森林与二叉树的转换（🍎🍎🍎）

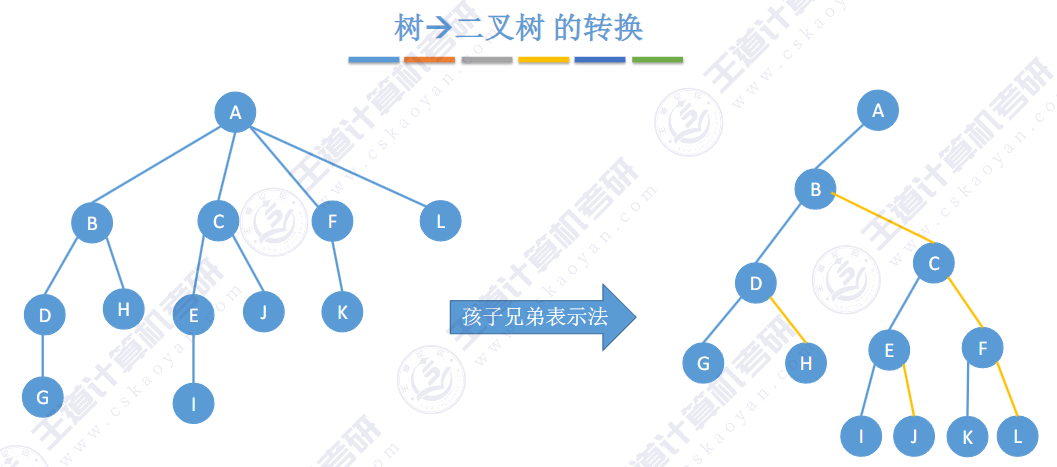
查找成功的次数：从根节点到目的结点经过的结点数

🚀5.4.3 树和森林的遍历

🏀5.5 树与二叉树的应用🍁

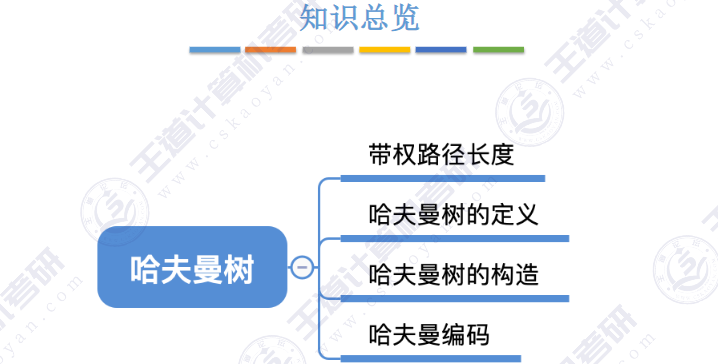
🚀5.5.1 哈夫曼树和哈夫曼编码

编码长度 = WPL

哈夫曼树压缩比

不能出现歧义（前缀问题,具有前缀特性）

比他小的只有1个，和他组成同一棵（相同的位于上面）

比他小的有两个，那么这两个组成另外一棵，从剩下的里面找最小的和他合并

结点数（2n - 1）：叶（n）+ 非叶（n-1）

节点数 = 度数 + 1

不能对已经标记的再添加子节点

可以编码的是叶子结点

在哈夫曼树的每个分支上标0或1
- 结点的左分支标0，右分支标1
- 把从根到每个叶子的路径上的标号连起来，作为该叶子代表的字符的编码

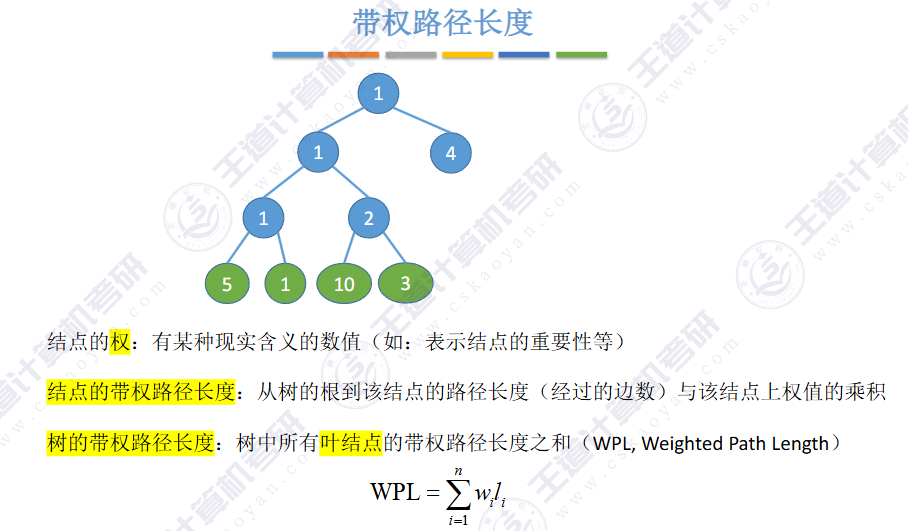
🚢带权路径长度（Weighted Path Length，WPL）

长度 = 边的个数

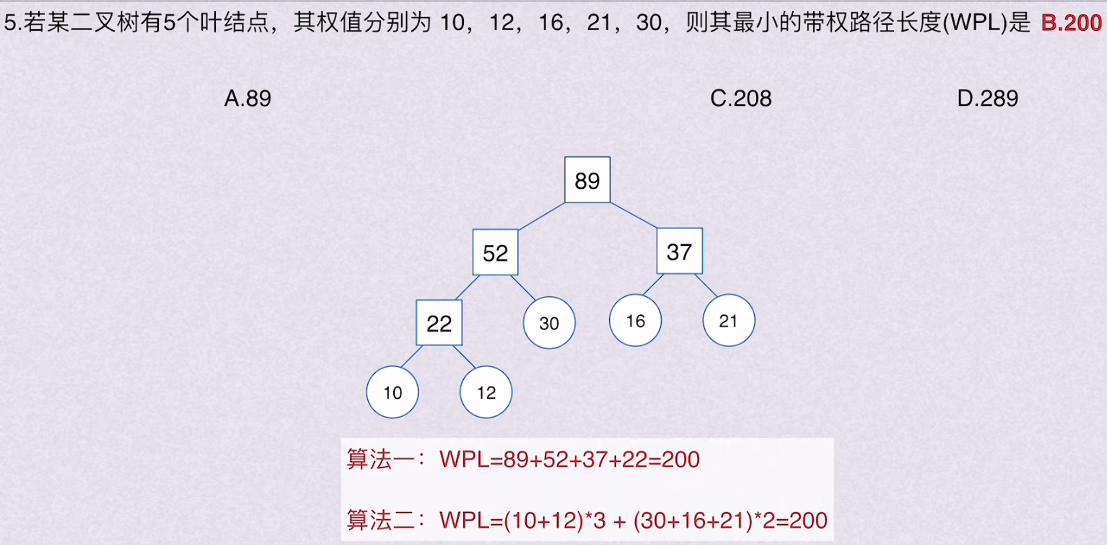
wpl唯一确定

树的WPL

🚢树的加权平均长度（23真题）

🚢带权路径长度最小的树 -- 哈夫曼树

也称 最优二叉树

等长编码；

出现次数最少得结点路径最短

不断地合并最小的两个

哈夫曼编码的基本思想是按照字符的频率构造一颗哈夫曼树，频率越高的字符，离根节点越近，并且规定位于节点左边的左孩子跟他父节点的边的权值为0，右边的为1，构造哈夫曼的过程是选取两个节点没有双亲并且权值最小的作为左右子树。

如下

频率2倍：高度很低，结点重复（相近的很多）

所以应该使用定长编码

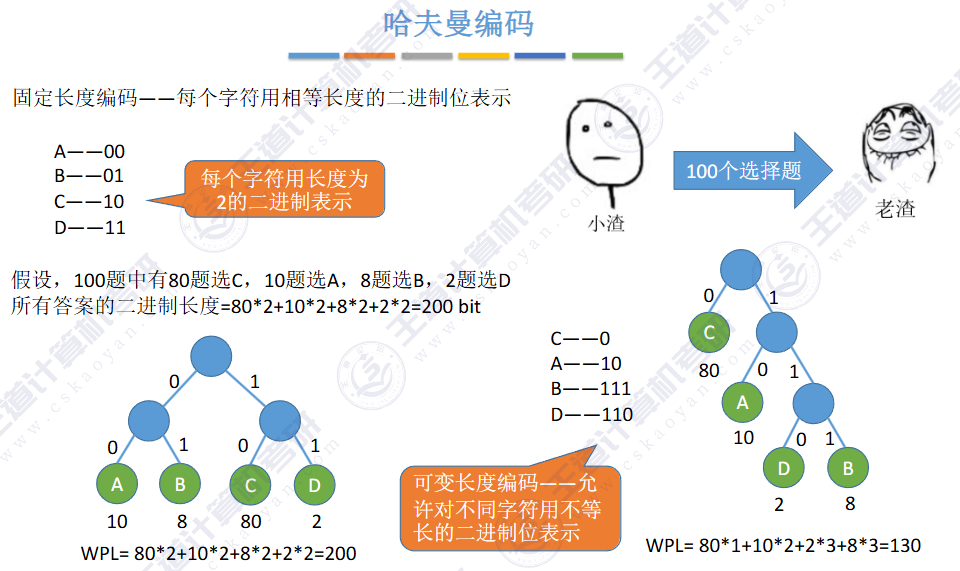
固定长度编码

        优点:每个字符对应的字符序列长度相同，易读取（不会产生二义性问题，依次往后按照固定长度读取即可得到字符）

缺点:计算机的传输资源（带宽）是有限的，如果每个字符都是等长的，当有的字符频率高，有的字符频率低，有的字符可能根本没出现，其实再使用等长编码就会浪费资源。



在这种编码下，如果文件内容是“ABCDEFGH"或者几个字符出现次数都比较均匀的情况下，这种编码方式其实也行，但是很多情况，有的字符频率会特别高，有的字符会特别低，如果整个都采用相同长度的编码，会浪费存储和传输资源。如果让那些频率高的字符对应存储的二进制序列长度短，而频率低的可以适当长一些，这样就可以大量减少资源的浪费了。

不定长度编码



        “编码不可以有二义性”：即一个字符的编码不可以是另外一个字符的前缀码，否则无法判断这是一个字符还是一个字符的一部分，比如：“01”和“010”就不能同时作为两个不同字符的编码。

        ”编码长度尽可能短"：让出现频率高的字符的编码长度短，而频率低的字符编码可以稍长；从而压缩总共的存储空间，提高传输的速度。

        优点：很明显，存储空间压缩，传输性能提升。

        缺点：设计时需考虑避免二义性问题。

不定长编码有多种，而如何设计，能让一段文字对应的编码长度总和最短呢？—— 哈夫曼编码：一种【贪心思想】的不定长编码策略，能使总编码长度最短。

编的树的分支线，0左1右

是一种前缀编码（彼此互不为前缀）--> 解码无歧义

可以用于数据压缩

最佳归并树

哈夫曼树 - - 二叉树

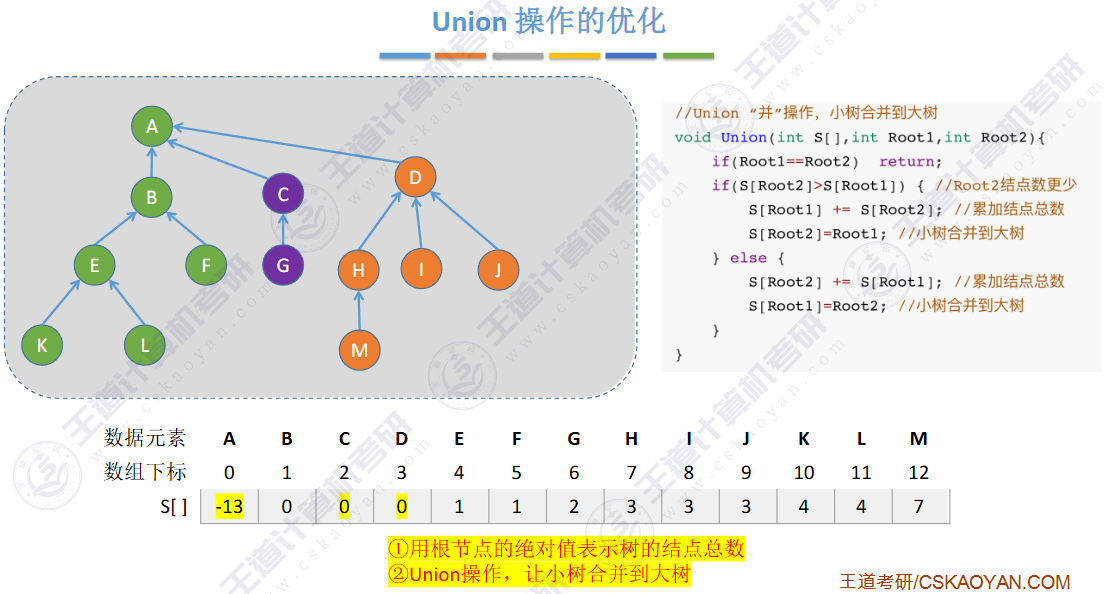
🚀5.5.2 并查集🍁

合并以后，root(10) = 1

find是路径压缩

逻辑结构是集合

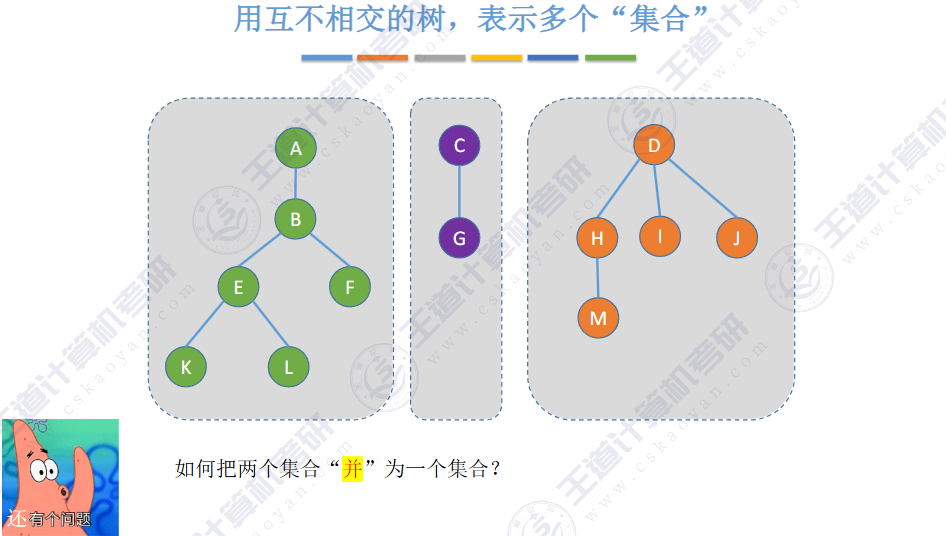
用互不相交的树，表示多个“集合

🚢如何“查”到一个元素到底属于哪一个集合？

从指定元素出发，一路向北，找到根节点

🚢如何判断两个元素是否属于同一个集合？

分别查到两个元素的根，判断根节点是否相同即可

🚢如何把两个集合“并”为一个集合？

让一棵树成为另一颗树的子树即可

小树合并到大树

🚢存储结构 🍁

双亲表示法

遍历的时候依次查找其根结点

【并查集的应用（检测环与连通性、实现kruskal）】 https://www.bilibili.com/video/BV1kJ4m1J7A7/?share_source=copy_web&vd_source=0caeacd6c3217ba41c56ea47a129e168

用树这种逻辑结构、数组这种物理结构来实现并查集。

访问到根，交换左右子树，额（白跑一趟）

【并查集的应用（检测环与连通性、实现kruskal）】 https://www.bilibili.com/video/BV1kJ4m1J7A7/?share_source=copy_web&vd_source=0caeacd6c3217ba41c56ea47a129e168

🚀优化

🚀总结🍁

IV确实要列举所有情况，然后进行遍历

📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌📌

向上

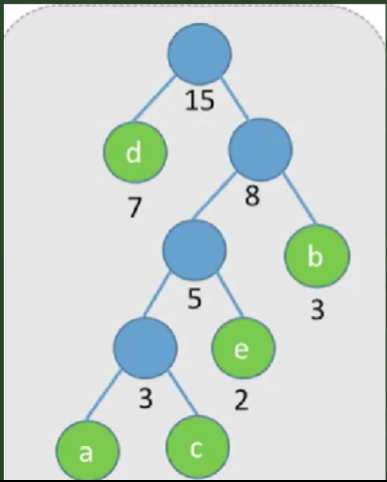
给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl) 达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)

按边计算路径

        (a) WPL=7x2+5x2+2x2+4x2 =36。

        (b) WPL=4x2+ 7x3+5x3+ 2x1=46。

        (c) WPL=7x1+5x2+2x3+4x3=35。

其中，图 5.25(c)树的 WPL 最小。可以验证，它恰好为哈夫曼树。

哈夫曼编码其实就是一种前缀编码

Q：什么是固定长度编码

A：在数据通信中，若对每个字符用相同的二进制位表示，称这种编码方式为固定长度编码。

🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁

因为每个字的二进制码长度一致

🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁🍁