理论推导:
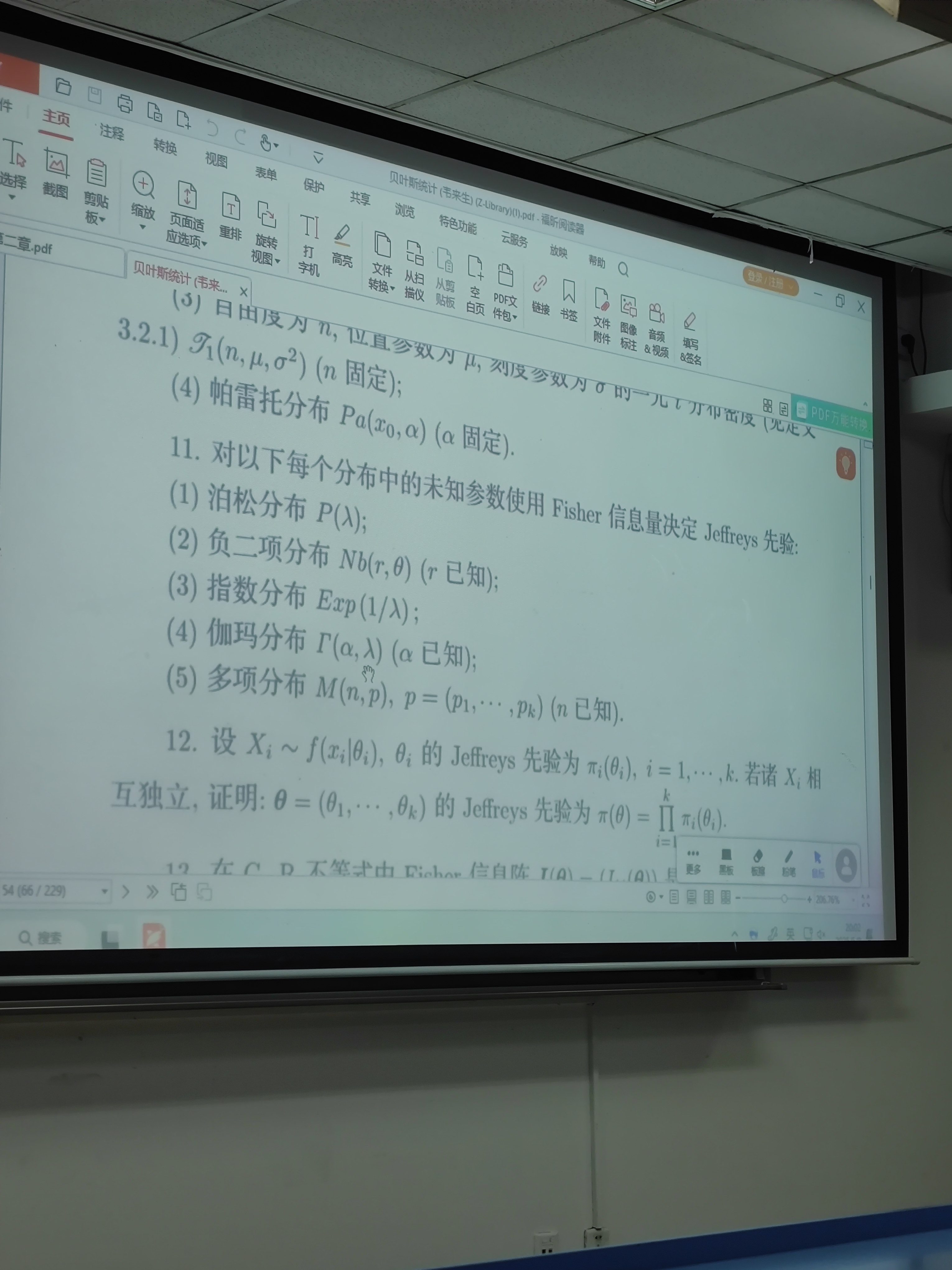
1. **泊松分布(Poisson Distribution)**:
泊松分布的参数是λ(lambda),其概率质量函数为P(X=k) = e^{-λ} λ^k /k! ,其中k=0,1,2,…。这里参数是λ,单参数的情况。
我需要先计算Fisher信息量I(λ),然后Jeffreys先验就是√I(λ)。
Fisher信息量的计算公式是对数似然的二阶导数的期望的负数,即对于单参数θ,I(θ) = -E[∂² log L(θ)/∂θ²],或者也可以用一阶导数的平方的期望,即I(θ) = E[(∂ log L(θ)/∂θ)^2]。不过对于泊松分布来说,可能用二阶导数更方便。
对数似然函数:对于一个观测值x,log L(λ) = -λ + x log λ - log(x!),所以导数一阶导数是d/dλ log L = -1 + x/λ。二阶导数是d²/dλ² log L = -x/λ²。然后Fisher信息量就是 -E[二阶导数],即E[x/λ²]。因为泊松分布的期望E[x] = λ,所以这里的期望值为 λ/λ² = 1/λ。因此,Fisher信息量I(λ) = 1/λ。
因此,Jeffreys先验是√I(λ) = √(1/λ) = λ^{-1/2},也就是1/√λ。所以Jeffreys先验为π(λ) ∝ 1/√λ。或者写成π(λ) = λ^{-1/2},忽略常数因子的话。
2. **负二项分布(Negative Binomial Distribution)**:
负二项分布的参数化可能有不同方式。一般来说,负二项分布可以表示为在成功概率为p的情况下,获得r次成功前的失败次数的分布。另一种参数化是使用均值μ和分散参数r。不过常见的参数是成功率p和预定的成功次数r。这里可能需要明确参数是哪一个。例如,当r已知时,参数是p;或者当r未知时,可能需要同时考虑两个参数。不过题目里应该指的是单参数情况,可能是p未知,而r已知,或者另一种情况。可能题目中需要明确,但这里可能假设参数是p,r是已知的。不过也有可能参数是r和p,但可能题目要求的是某个参数的情况。我需要再仔细想想。
可能负二项分布的参数化方式不同,需要确认。例如,概率质量函数可以写成P(X=k) = C(k + r -1, k) p^r (1-p)^k,其中k=0,1,2,…,这里参数是p,而r是已知的。或者另一种参数化,比如以均值μ和分散参数r,如P(X=k) = Γ(r +k)/(Γ(r)k!) (r/(r+μ))^r (μ/(r+μ))^k,其中参数是μ,r是已知的。
题目中可能需要明确参数是什么,但可能假设的是传统的参数p(成功的概率),未知参数是p,而r是已知的。所以假设这里参数是p,其他参数已知的情况下,计算Fisher信息量。
对数似然函数对于一个观测值k是log L(p) = log Γ(k + r) - log Γ(r) - log k! + r log p + k log(1 - p).
一阶导数是d/dp log L = r/p - k/(1 - p).
二阶导数是d²/dp² log L = -r/p² - k/(1 - p)^2.
Fisher信息量I(p) = -E[二阶导数] = E[r/p² + k/(1 - p)^2].
这里k服从负二项分布,其期望E[k] = r(1 - p)/p。所以代入:
I(p) = r/p² + E[k]/(1 - p)^2 = r/p² + [r(1 - p)/p]/(1 - p)^2 = r/p² + r(1 - p)/[p (1 - p)^2] = r/p² + r/(p(1 - p)).
合并项:r/(p²) + r/(p(1-p)) = r[1/(p²) + 1/(p(1-p))] = r[ (1 - p) + p ] / [p²(1 - p)] ) = r[1] / [p²(1 - p)] ].
所以I(p) = r / [p²(1 - p)].
因此Jeffreys先验是√I(p) = √[r / (p²(1 - p)) ] = √r / [p √(1 - p)].
但因为r是已知的常数,Jeffreys先验可以忽略常数因子,所以π(p) ∝ 1/[p √(1 - p)].
但需要检查是否正确。或者可能参数是另一个参数化,例如参数为r和p,但这里可能题目中要求的是单参数情况。可能需要进一步确认。不过如果题目中的负二项分布参数是另一个参数化,比如以均值μ,那么可能会有不同的结果。
例如,在另一种参数化下,负二项分布的均值为μ = r(1-p)/p,方差为μ + μ²/r。这种情况下,如果参数是μ,而r是已知的,那么可能需要重新计算。
但可能题目中的负二项分布参数是传统的成功概率p,所以这里的结果是π(p) ∝ 1/[p √(1 - p)]。不过可能需要再检查一下计算过程是否正确。
另外,在计算Fisher信息量时,是否有可能哪里出错了?
比如,对于负二项分布的概率质量函数是P(k) = C(k + r -1, k) p^r (1 - p)^k,那么对数似然函数是log L = log C(k + r -1, k) + r log p + k log(1 - p).
一阶导数是d/dp log L = r/p - k/(1 - p).
二阶导数是d²/dp² log L = -r/p² - k/(1 - p)^2.
期望值E[二阶导数] = -r/p² - E[k]/(1 - p)^2.
而E[k] = r(1 - p)/p,所以代入:
-r/p² - [r(1 - p)/p]/(1 - p)^2 = -r/p² - r/[p(1 - p)].
因此,Fisher信息量I(p) = -E[二阶导数] = r/p² + r/[p(1 - p)].
这个和之前的计算一样,合并之后得到r/[p²(1 - p)],所以Jeffreys先验就是sqrt(r/(p²(1 - p))) = sqrt(r) / [p sqrt(1 - p)].
由于Jeffreys先验在常数因子下是不考虑的,所以可以写成π(p) ∝ 1/[p sqrt(1 - p)].
所以负二项分布的情况下的Jeffreys先验是1/[p sqrt(1 - p)],比例常数省略。
3. **指数分布(Exponential Distribution)**:
指数分布的参数通常是率参数λ(或者有时用θ=1/λ作为尺度参数)。概率密度函数为f(x|λ) = λ e^{-λ x},x ≥ 0.
参数是λ,单参数情况。
对数似然函数:log L(λ) = log λ - λ x.
一阶导数:d/dλ log L = 1/λ - x.
二阶导数:d²/dλ² log L = -1/λ².
Fisher信息量I(λ) = -E[二阶导数] = 1/λ².
因此,Jeffreys先验是sqrt(I(λ)) = 1/λ.
所以Jeffreys先验为π(λ) ∝ 1/λ,即π(λ) = 1/λ(忽略常数因子)。这也称为尺度参数的Jeffreys先验,符合预期。
4. **伽马分布(Gamma Distribution)**:
伽马分布通常有两个参数:形状参数k(或α)和尺度参数θ(或β的倒数)。有时也参数化为形状α和率参数β=1/θ。题目中可能需要确定哪个参数是未知参数,是单参数还是双参数的情况。不过题目中提到的是对未知参数使用Fisher信息量,所以如果伽马分布有两个未知参数,则需要计算多参数的Jeffreys先验,即Fisher信息矩阵的行列式的平方根。如果只有一个参数未知,另一个已知,则按照单参数处理。
但题目中可能假设两个参数都是未知的?或者题目是否指定了哪个参数是未知的?题目里可能没有明确说明,可能需要进一步明确。
例如,假设伽马分布的参数是形状参数α和尺度参数β,都是未知的,那么需要计算双参数的Jeffreys先验。或者可能题目中指的是单参数的情况,例如已知其中一个参数,另一个未知?但题目里没有说明,可能需要假设两种情况都是可能的,但根据常见的例子,可能伽马分布在这里可能需要考虑两参数的情况。
但根据题目中的描述,“对下面每个分布的未知参数”,可能每个分布可能有不同的未知参数数目。例如,指数分布可以视为伽马分布的一个特例(形状参数为1),但这里的伽马分布应该是一般情况下的两参数伽马分布,所以需要处理两参数的Jeffreys先验。
伽马分布的概率密度函数是f(x|α, β) = β^α x^{α - 1} e^{-β x} / Γ(α),其中x > 0,形状参数α > 0,率参数β > 0。
这里参数是θ = (α, β),两者都是未知的。需要计算Fisher信息矩阵,然后求其行列式的平方根。
对数似然函数为log L(α, β) = α log β + (α - 1) log x - β x - log Γ(α).
首先,计算各个二阶偏导数,然后求期望,得到Fisher信息矩阵。
首先,计算一阶导数:
∂/∂α log L = log β + log x - ψ(α),其中ψ(α)是digamma函数,即Γ’(α)/Γ(α).
∂/∂β log L = α/β - x.
然后计算二阶导数:
∂²/(∂α²) log L = -ψ’(α),即-trigamma函数。
∂²/(∂β²) log L = -α/β².
交叉导数:
∂²/(∂α∂β) log L = 1/β.
因此,Fisher信息矩阵I(α, β)的元素为:
I_αα = -E[∂²/(∂α²) log L] = ψ’(α),
I_ββ = -E[∂²/(∂β²) log L] = α/β²,
I_αβ = I_βα = -E[∂²/(∂α∂β) log L] = -E[1/β] = -1/β,但这里需要确认是否正确,因为E[1/β]其实就是1/β,因为β是参数,不是随机变量。或者是否在计算Fisher信息时是否应该考虑变量的期望?
或许需要重新检查交叉项的期望:
∂²/(∂α∂β) log L = 1/β,
因此,Fisher信息矩阵中的交叉项I_αβ = -E[∂²/(∂α∂β) log L] = -E[1/β] = -1/β,对吗?或者是否应该是计算协方差?
其实,正确的计算方式应该是计算期望的负数,但二阶混合导数在这里的表达式是否含有随机变量x?
在二阶导数∂²/(∂α∂β) log L的表达式中,是否有依赖于x的部分?
原一阶导数是∂/∂α log L = log β + log x - ψ(α),
所以当对β求导时,得到∂²/(∂α∂β) log L = 1/β.
这个二阶导数并不依赖于x,因此其期望就是它本身,所以I_αβ = -E[∂²/(∂α∂β) log L] = -1/β.
同样,I_βα = -1/β.
而I_αα是ψ’(α),I_ββ是α/β².
所以,Fisher信息矩阵是:
[ ψ’(α) -1/β ]
[ -1/β α/β² ]
计算这个矩阵的行列式:
det(I) = ψ’(α) * (α/β²) - (-1/β)^2 = (α ψ’(α))/β² - 1/β² = [α ψ’(α) - 1]/β².
所以Jeffreys先验是这个行列式的平方根,即sqrt([α ψ’(α) - 1]/β²) = sqrt(α ψ’(α) - 1)/β.
因此,Jeffreys先验为π(α, β) ∝ sqrt(α ψ’(α) - 1)/β.
这个结果看起来比较复杂,可能在某些情况下可以简化吗?例如,是否有特定的关系式?
但看起来这就是伽马分布当两个参数都是未知时的Jeffreys先验。不过这可能是否正确需要进一步验证,因为我在计算过程中可能哪里出错了。
例如,在计算交叉项的时候,是否正确?
另外,在计算I_αβ时,是否正确?
另一个方法是使用原始的对数似然的二阶导数:
∂²/(∂α∂β) log L = ∂/∂β (∂/∂α log L) = ∂/∂β (log β + log x - ψ(α)) = 1/β.
因此,这个二阶导数是1/β,不依赖于x,因此其期望就是1/β。因此,Fisher信息矩阵中的交叉项I_αβ = -E[∂²/(∂α∂β) log L] = -1/β。
因此,矩阵是正确的。
因此,行列式是[ψ’(α) * (α/β²)] - [(-1/β)^2] = (α ψ’(α)/β²) - (1/β²) = (α ψ’(α) - 1)/β².
所以行列式的平方根是sqrt(α ψ’(α) - 1)/β.
所以Jeffreys先验是π(α, β) ∝ sqrt(α ψ’(α) - 1)/β.
这个结果看起来对吗?有没有可能我哪里出错了?
另外,在文献中,是否有伽马分布的Jeffreys先验的已知结果?
例如,根据参考资料,伽马分布的形状参数α和尺度参数β的Jeffreys先验可能为π(α, β) ∝ sqrt(α ψ’(α) - 1)/β,这似乎符合这里的计算。但可能在某些情况下,这个表达式可以进一步简化,不过看起来这里无法进一步简化,所以可能答案就是这样。
5. **多项分布(Multinomial Distribution)**:
多项分布的参数是各个类别的概率向量p = (p1, p2, ..., pk),其中Σpi = 1,且pi > 0。这里参数有k-1个自由参数,因为最后一个概率pk = 1 - p1 - ... - pk-1.
因此,参数是θ = (p1, p2, ..., pk-1),维度为k-1。因此,需要计算(k-1)×(k-1)的Fisher信息矩阵,然后求行列式的平方根。
多项分布的概率质量函数是P(x1, x2, ..., xk) = n!/(x1!x2!...xk!) p1^{x1} p2^{x2} ... pk^{xk},其中Σxi = n.
对数似然函数为log L(p) = Σxi log pi + 常数项。
由于参数有约束条件Σpi = 1,通常使用拉格朗日乘数法来处理,但计算Fisher信息矩阵时需要注意参数的冗余性,通常我们会选择前k-1个参数作为自由参数,然后pk = 1 - Σ_{i=1}^{k-1} pi。
对于多项分布的Fisher信息矩阵,其元素I(p)_{i,j} = n ( δ_{ij}/pi + 1/pk ),其中δ_{ij}是Kronecker delta函数,当i=j时为1,否则为0。或者另一种形式?
另一种计算方法是,考虑每个观测是一个类别,多项分布的一次试验(n=1)的对数似然为log L = Σ_{i=1}^k xi log pi,其中xi是one-hot向量。对于n次独立试验(但多项分布通常视为单次试验有n次独立分类,但多项分布实际上是n次试验中各类别计数的分布),不过这里Fisher信息量通常是针对单个观测的,即n=1的情况,然后乘以n得到总的信息量。但Jeffreys先验不依赖于样本量,所以可能只需要考虑单个观测的情况。
对于单个观测,即n=1,此时x是一个单位向量,其中第i个位置为1,其他为0,对应概率pi。
对数似然函数对于参数p1, ..., pk-1来说,可以表示为log L = Σ_{i=1}^{k-1} xi log pi + xk log (1 - Σ_{i=1}^{k-1} pi).
因此,对于参数pj(j=1到k-1),其一阶导数为:
∂ log L / ∂ pj = xj/pj - xk/pk.
然后二阶导数为:
当i = j时,二阶导数为 -xj/pj² - xk/pk².
当i ≠ j时,二阶导数为 -xk/pk².
但需要计算期望值。因为对于单个观测,xj是伯努利变量,取1的概率为pj,否则为0,同时xk = 1 - Σ_{i=1}^{k-1} xi,当其他xi都为0时,xk=1。
因此,E[xj] = pj,E[xk] = pk.
计算Fisher信息矩阵的元素I_ij = Cov(∂ log L/∂ pi, ∂ log L/∂ pj).
或者根据另一种方法,Fisher信息矩阵的元素I_ij = -E[∂² log L / ∂ pi ∂ pj].
因此,首先计算二阶导数:
∂² log L / ∂ pi ∂ pj = - δ_{ij} xi / pi² - xk / pk².
但这里的xk = 1 - Σ xi,当n=1时,只有一个xi为1,其余为0。所以当计算期望时,E[∂² log L / ∂ pi ∂ pj] = - δ_{ij} E[xi / pi²] - E[xk / pk²].
当i ≠ j时,δ_{ij}=0,所以E[∂² log L / ∂ pi ∂ pj] = - E[xk / pk²] = - (pk / pk²) = -1/pk.
当i = j时,E[∂² log L / ∂ pi²] = - E[xi / pi²] - E[xk / pk²] = - (pi / pi²) - (pk / pk²) = -1/pi - 1/pk.
因此,Fisher信息矩阵的元素为:
I_ij = -E[∂² log L / ∂ pi ∂ pj] = δ_{ij}(1/pi + 1/pk) + (1 - δ_{ij})(1/pk).
或者可以写成:
I_ij = δ_{ij}/pi + 1/pk,对于i, j = 1, ..., k-1.
因此,Fisher信息矩阵是一个(k-1)×(k-1)矩阵,其中对角线元素为1/pi + 1/pk,非对角线元素为1/pk.
这个矩阵的行列式是什么?计算这个行列式可能比较复杂,但有一个已知的结果,对于多项分布,Jeffreys先验是Dirichlet分布,参数为(1/2, 1/2, ..., 1/2)。也就是说,π(p) ∝ ∏_{i=1}^k pi^{-1/2},也就是1/√(p1 p2 ... pk).
不过,这里需要验证是否行列式的平方根确实对应于这个结果。
另一种方法是,对于多项分布的Fisher信息矩阵,其行列式已知为 (n^{k-1} ) / (p1 p2 ... pk)),但可能对于单个观测的情况,n=1,则行列式为 1/(p1 p2 ... pk).
但是这里的计算可能更复杂,因为矩阵的结构是每个对角元素是1/pi + 1/pk,非对角元素是1/pk.
或许可以使用矩阵行列式的公式来求解。例如,对于这样的结构,可以将矩阵分解为一个对角矩阵加上一个秩一矩阵。
令D为对角矩阵,其中D_ii = 1/pi,i=1,...,k-1.
然后,矩阵I可以表示为D + (1/pk) * 11^T,其中1是k-1维的全1向量。
根据矩阵行列式引理,det(D + u v^T) = det(D) (1 + v^T D^{-1} u).
这里,u = v = sqrt(1/pk) * 1,不过可能需要调整。
不过更准确地说,矩阵是D + (1/pk) * 11^T,其中D是对角矩阵,元素为1/pi,i=1,...,k-1.
所以根据矩阵行列式引理,det(D + (1/pk) 11^T) = det(D) * [1 + (1/pk) 1^T D^{-1} 1].
计算det(D) = ∏_{i=1}^{k-1} (1/pi).
然后,计算1^T D^{-1} 1 = Σ_{i=1}^{k-1} (1/(1/pi)) ) = Σ_{i=1}^{k-1} pi.
因为Σ_{i=1}^k pi = 1,所以Σ_{i=1}^{k-1} pi = 1 - pk.
因此,行列式det(I) = ∏_{i=1}^{k-1} (1/pi) * [1 + (1/pk)(1 - pk)] = ∏_{i=1}^{k-1} (1/pi) * [1 + (1 - pk)/pk] = ∏_{i=1}^{k-1} (1/pi) * [ (pk + 1 - pk)/pk ) ] = ∏_{i=1}^{k-1} (1/pi) * (1/pk) ) = ∏_{i=1}^k (1/pi) ),因为pk是第k个概率,所以总共有k个项,而这里的行列式是前k-1个参数的信息矩阵的行列式,结果是∏_{i=1}^k (1/pi) )。
所以det(I) = 1/(p1 p2 ... pk).
因此,Jeffreys先验是sqrt(det(I)) = 1/√(p1 p2 ... pk).
所以π(p) ∝ 1/√(p1 p2 ... pk),即Dirichlet分布参数为(1/2, 1/2, ..., 1/2)。
因此,多项分布的Jeffreys先验是Dirichlet(1/2, ..., 1/2),即π(p1, ..., pk) ∝ ∏_{i=1}^k pi^{-1/2}。
因此,答案是这个。
总结各个分布的结果:
1. 泊松分布(λ): π(λ) ∝ λ^{-1/2}
2. 负二项分布(p): π(p) ∝ [p²(1 - p)]^{-1/2} → 1/(p √(1 - p))
3. 指数分布(λ): π(λ) ∝ 1/λ
4. 伽马分布(α, β): π(α, β) ∝ sqrt(α ψ’(α) - 1)/β
5. 多项分布(p1,...,pk): π(p) ∝ ∏_{i=1}^k pi^{-1/2}
需要检查是否有错误,比如在负二项分布部分,是否正确处理了参数?
另外,伽马分布的Jeffreys先验是否有可能在某个参数固定时更简单?例如,当形状参数α已知时,尺度参数β的Jeffreys先验会是怎样的?但题目中并未指定参数是否已知,因此需要假设题目中的伽马分布的两个参数都是未知的,因此得到上述结果。
同样,对于负二项分布,如果参数是r和p,其中两者都是未知的,可能需要重新计算两参数的Fisher信息矩阵,但这可能超出了题目的要求。但题目中说“未知参数”,可能假设负二项分布只有一个参数未知,另一个已知。比如在问题中,可能负二项分布的参数是r已知,p未知,或者反之。但根据我之前的计算,假设参数是p,r已知的情况下得到的Jeffreys先验是1/(p √(1 - p))。而如果参数是r,而p已知,可能需要另外计算,但题目中没有说明,所以可能正确的情况是参数为p,r已知,因此得到上述结果。
综上,这些应该就是各个分布的Jeffreys先验。把你的思考过程转化成详细的推导过程。
以下是针对每个分布的 **Jeffreys 先验** 的详细推导过程,基于 **Fisher 信息量** 的计算。
---
## 1. 泊松分布(Poisson Distribution)
**参数**:\(\lambda\)(强度参数)
**概率质量函数**:
\[
P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}, \quad k = 0, 1, 2, \dots
\]
### 步骤:
1. **对数似然函数**:
\[
\log L(\lambda) = -\lambda + k \log \lambda - \log(k!)
\]
2. **一阶导数**:
\[
\frac{d}{d\lambda} \log L = -1 + \frac{k}{\lambda}
\]
3. **二阶导数**:
\[
\frac{d^2}{d\lambda^2} \log L = -\frac{k}{\lambda^2}
\]
4. **Fisher 信息量**:
\[
I(\lambda) = -E\left[\frac{d^2}{d\lambda^2} \log L\right] = E\left[\frac{k}{\lambda^2}\right] = \frac{\lambda}{\lambda^2} = \frac{1}{\lambda}
\]
(因为 \(E[k] = \lambda\))
5. **Jeffreys 先验**:
\[
\pi(\lambda) \propto \sqrt{I(\lambda)} = \lambda^{-1/2}
\]
### 结果:
\[
\boxed{\pi(\lambda) \propto \frac{1}{\sqrt{\lambda}}
\]
---
## 2. 负二项分布(Negative Binomial Distribution)
**参数**:\(p\)(成功概率),\(r\) 已知
**概率质量函数**:
\[
P(X = k) = \binom{k + r - 1}{k} p^r (1 - p)^k, \quad k = 0, 1, 2, \dots
\]
### 步骤:
1. **对数似然函数**:
\[
\log L(p) = \log \Gamma(k + r) - \log \Gamma(r) - \log(k!) + r \log p + k \log(1 - p)
\]
2. **一阶导数**:
\[
\frac{d}{dp} \log L = \frac{r}{p} - \frac{k}{1 - p}
\]
3. **二阶导数**:
\[
\frac{d^2}{dp^2} \log L = -\frac{r}{p^2} - \frac{k}{(1 - p)^2}
\]
4. **Fisher 信息量**:
\[
I(p) = -E\left[\frac{d^2}{dp^2} \log L\right] = \frac{r}{p^2} + \frac{E[k]}{(1 - p)^2}
\]
由于 \(E[k] = \frac{r(1 - p)}{p}\),代入得:
\[
I(p) = \frac{r}{p^2} + \frac{r(1 - p)}{p(1 - p)^2} = \frac{r}{p^2(1 - p)}
\]
5. **Jeffreys 先验**:
\[
\pi(p) \propto \sqrt{I(p)} = \frac{\sqrt{r}}{p \sqrt{1 - p}} \propto \frac{1}{p \sqrt{1 - p}}
\]
(忽略常数 \(\sqrt{r}\))
### 结果:
\[
\boxed{\pi(p) \propto \frac{1}{p \sqrt{1 - p}}
\]
---
## 3. 指数分布(Exponential Distribution)
**参数**:\(\lambda\)(率参数)
**概率密度函数**:
\[
f(x \mid \lambda) = \lambda e^{-\lambda x}, \quad x \geq 0
\]
### 步骤:
1. **对数似然函数**:
\[
\log L(\lambda) = \log \lambda - \lambda x
\]
2. **一阶导数**:
\[
\frac{d}{d\lambda} \log L = \frac{1}{\lambda} - x
\]
3. **二阶导数**:
\[
\frac{d^2}{d\lambda^2} \log L = -\frac{1}{\lambda^2}
\]
4. **Fisher 信息量**:
\[
I(\lambda) = -E\left[\frac{d^2}{d\lambda^2} \log L\right] = \frac{1}{\lambda^2}
\]
5. **Jeffreys 先验**:
\[
\pi(\lambda) \propto \sqrt{I(\lambda)} = \frac{1}{\lambda}
\]
### 结果:
\[
\boxed{\pi(\lambda) \propto \frac{1}{\lambda}}
\]
---
## 4. 伽马分布(Gamma Distribution)
**参数**:\(\alpha\)(形状参数),\(\beta\)(率参数)
**概率密度函数**:
\[
f(x \mid \alpha, \beta) = \frac{\beta^\alpha x^{\alpha - 1} e^{-\beta x}}{\Gamma(\alpha)}, \quad x > 0
\]
### 步骤:
1. **对数似然函数**:
\[
\log L(\alpha, \beta) = \alpha \log \beta + (\alpha - 1) \log x - \beta x - \log \Gamma(\alpha)
\]
2. **二阶导数**:
- \(\frac{\partial^2}{\partial \alpha^2} \log L = -\psi'(\alpha)\)(\(\psi'\) 是 trigamma 函数)
- \(\frac{\partial^2}{\partial \beta^2} \log L = -\frac{\alpha}{\beta^2}\)
- \(\frac{\partial^2}{\partial \alpha \partial \beta} \log L = \frac{1}{\beta}\)
3. **Fisher 信息矩阵**:
\[
I(\alpha, \beta) = \begin{pmatrix}
\psi'(\alpha) & -\frac{1}{\beta} \\
-\frac{1}{\beta} & \frac{\alpha}{\beta^2}
\end{pmatrix}
\]
4. **行列式**:
\[
\det(I) = \psi'(\alpha) \cdot \frac{\alpha}{\beta^2} - \left(-\frac{1}{\beta}\right)^2 = \frac{\alpha \psi'(\alpha) - 1}{\beta^2}
\]
5. **Jeffreys 先验**:
\[
\pi(\alpha, \beta) \propto \sqrt{\det(I)} = \frac{\sqrt{\alpha \psi'(\alpha) - 1}}{\beta}
\]
### 结果:
\[
\boxed{\pi(\alpha, \beta) \propto \frac{\sqrt{\alpha \psi'(\alpha) - 1}}{\beta}}
\]
---
## 5. 多项分布(Multinomial Distribution)
**参数**:\(\mathbf{p} = (p_1, \dots, p_k)\)(概率向量),\(\sum_{i=1}^k p_i = 1\)
**概率质量函数**:
\[
P(X_1 = x_1, \dots, X_k = x_k) = \frac{n!}{x_1! \cdots x_k!} p_1^{x_1} \cdots p_k^{x_k}
\]
### 步骤:
1. **对数似然函数**(单观测,\(n = 1\)):
\[
\log L(\mathbf{p}) = \sum_{i=1}^k x_i \log p_i
\]
2. **Fisher 信息矩阵**(对 \(p_1, \dots, p_{k-1}\)):
- 对角线元素:\(I_{ii} = \frac{1}{p_i} + \frac{1}{p_k}\)
- 非对角线元素:\(I_{ij} = \frac{1}{p_k}\)
3. **行列式**:
\[
\det(I) = \frac{1}{p_1 p_2 \cdots p_k}
\]
4. **Jeffreys 先验**:
\[
\pi(\mathbf{p}) \propto \sqrt{\det(I)} = \prod_{i=1}^k p_i^{-1/2}
\]
### 结果:
\[
\boxed{\pi(\mathbf{p}) \propto \prod_{i=1}^k \frac{1}{\sqrt{p_i}}}
\]
---
## 总结
| 分布 | Jeffreys 先验 |
|----------------|-----------------------------------------------|
| 泊松分布 | \(\pi(\lambda) \propto \lambda^{-1/2}\) |
| 负二项分布 | \(\pi(p) \propto \frac{1}{p \sqrt{1 - p}}\) |
| 指数分布 | \(\pi(\lambda) \propto \lambda^{-1}\) |
| 伽马分布 | \(\pi(\alpha, \beta) \propto \frac{\sqrt{\alpha \psi'(\alpha) - 1}}{\beta}\) |
| 多项分布 | \(\pi(\mathbf{p}) \propto \prod_{i=1}^k p_i^{-1/2}\) |






















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








