各项符号的意义






各类函数的图像
lnx的图像

e的x次幂的图像


e的1/x次幂的图像

tan x 函数图像

cot x 函数图像

sin 1/x 函数图像

cos 1/x 函数图像

arc sinx 函数图像

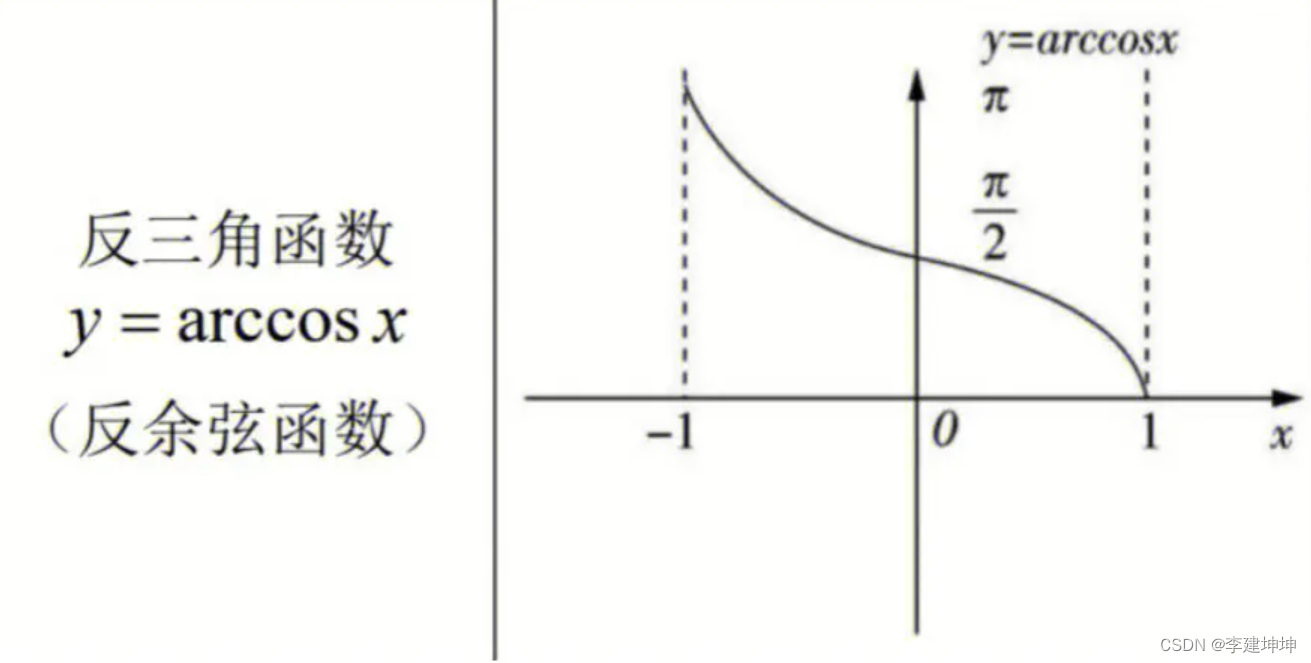
arc cos x 函数图像
arc tan x 函数图像

arc cot x 函数图像

常见公式
lim x→0 (1-cos x) = 1/2 x²
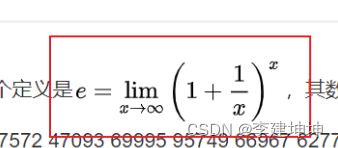
函数

复合函数的概念

反函数的概念

反函数例题

求反函数的方法

初等函数是什么

对数函数概念

三角函数以及反三角函数的概念

函数的单调性


函数的奇偶性

函数的周期性


函数例题



极限


极限例题


补充说明:解题3中,是利用了e的性质来解的

证明极限例题
 在证明命题1之前,首先需要知道一个定理,即| |a| - |b| | <= | a-b |
在证明命题1之前,首先需要知道一个定理,即| |a| - |b| | <= | a-b |



自变量趋于无穷时函数的极限


注意,n→∞ 等价于 n→+∞
因为n默认认为是数列下标,为正整数

自变量趋于有限时函数的极限

左极限与右极限

这里要注意区分e的无穷

三种需要区分左右极限的问题

同理,arctan x 也是没有极限的,但是分左右之后可以有两个极限

区分左右极限例题


左右极限证明题

该题关键在于记住两个公式,然后就是极限存在则证明两段极限相等

收敛与发散
数列收敛,等价于数列存在极限

数列发散,等价于数列不存在极限,不存在极限有两种情况:极限为∞,极限有多个
数列组合的变换

收敛数列相加减,相乘,结果都是收敛数列
收敛数据与发散数列想加减,结果是发散数列,但相乘,结果是不确定的,可能是收敛数列,也可能是发散数列,见红色圈中表达式

发散数列与发散数列相加减,结果是不确定的,如上方红框
相乘也是不确定的,如下方红框
数列极限的有界性

收敛必有界
有界未必收敛
比如 -1的n次幂
发散未必无界 比如 {-1,1,-1,1,…}
无界必发散
函数极限的有界性


即局部有界不能推出极限存在

如 f(x) = sin 1/x 在 【-1,1】之间是局部有界的,但是没有极限
数列极限的保号性

注意结论1中,Xn > 0 而 ≠ 0,因为 可以由反例 (-1的n次方)/ n 趋近于0可知,它是一左一右,一正一负跳着趋近于0的,所以不成立
注意结论2中,Xn ≥ 0 而不能只>0,因为由反例1/n可知,当n>0时,极限为0,所以不成立
函数极限的保号性

函数极限保号性例题


极限值与无穷小的关系

极限存在准则之夹逼准则

极限存在准则之单调有界准则

夹逼准则例题


上题中要注意,方框中是取整函数的性质,可以直接拿来用

上题中方框部分可以明显得出那部分小于1,所以看作1时,整体式子最大
单调有界准则习题

无穷小量

无穷小量例题


这道题的关键在于有个公式 ,即 lim x→0 (1-cos x) = 1/2 x²
还有就是当a(x) 与 sin(x) 极限都为0 时,可以带入到原来的式子中
注意:最后写错了,应该是为常数且≠1
无穷小的性质

有限个无穷小的和仍然是无穷小
但是无限个无穷小的和就不是无穷小了
看右面那个框框,结果为1/2,是常量了,就是因为他有n项,即无穷项
无穷小的性质例题

无穷大量

常用的一些无穷大量的比较

<<为远小于号
后面的/前面的极限为0 ,前面的/后面的极限为∞
无穷大量例题

根据上面的公式,直接选择C ,超级简单
无穷大量的性质

注意:
1.无穷大和无穷大的和并不为无穷大,比如 -∞ 和+∞
2.无穷大乘有界并不为无穷大,例如对于有界量(1/n)来说,无穷大是n ,则乘积为1,对于无穷大根号n来说,乘积是 0 ,对于无穷大n来说,乘积是∞,所以它是不确定的
无穷大量与无界变量的关系

无穷大无穷小例题

无穷大量与无穷小量的关系

极限的概念/性质/存在准则

数列 {Xn} 收敛于 a 表示对于任意给定的正实数ε,存在一个正整数 N,当 n>N 时,| Xn - a | < ε 成立。
这个题就变成了
| Xn - a | < ε 和
| Xn - a | <= 2ε
能否互相推论的问题。
因为ε是一个无限趋近于0的数字,所以2ε是没有意义的,它和ε一样都代表无限趋近于0的一个数字,又因为ε≠0,所以两个条件相同

这道题用到了之前学习的极限的奇偶性,
A选项中,数列极限的奇数列和偶数列同时取同一个极限时,则整个数列取这个极限。
B选项和D选项的差别在于,B选项包含了所有数列,而D选项中还差3n+2这个项
C选项中反着推怎么都是对的。

1/x²的图像是这样的

所以 lim x→0 1/x² = +∞
sin 1/x 的图像是这样的

所以 lim x→0 sin(1/x) 没有极限,但是处于∈[-1,1]
A选项,无穷小,
由于 1/x²是无穷大,sin (1/x) 如果取1的时候,结果就是无穷大了,所以不成立
B选项,无穷大,
由于 1/x²是无穷大,sin (1/x) 如果取0的时候,结果就是0了,所以不成立
C选项,有界但不是无穷小,
由于 1/x²是无穷大,sin (1/x) 如果取1的时候,结果就是无穷大了,所以不成立

像这种题,只要找sin图像中特殊的点,就能作答
求极限的8种方法

利用基本极限求极限
常用的基本极限

注意上面板书的那两个极限不存在
只有在x→0+以及x→+∞的时候才有极限

极限为1,这俩和上边的区别为,上边为无穷小的无穷大次幂,下边为无穷大的无穷小次幂,所以极限不同


1的无穷大次方


注意板书中红框中是错的,红框中的算式应该是下面的结果
这道题用到了两个基本极限


注意,这道题如果写成上面这种形式就是正确的了
这时候的P是个常数,而不是n,n是趋向于无穷的
1的常数次幂是1,而1的无穷次幂是不确定的

这道题利用的是上面的1的无穷大次幂三步走的方法

用排除法更简单,要点还是要了解1的无穷大次幂那个知识点

利用等价无穷小代换求极限

注意,这里面的波浪线是等价于的意思

可以通过如下方式证明这个结论

常用的等价无穷小替换

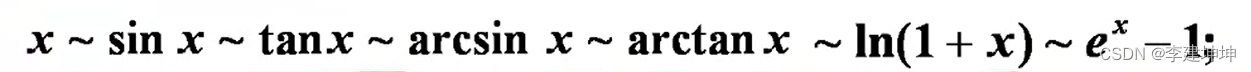


这两个蓝色的可以这样用洛必达证明得来



























 1493
1493

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








