
使用MCSDK配置基于STM32的电机控制工程,里面会自动配置很多参数。其中就有电流环的PI控制参数。FOC控制的情况下,默认是Id=0的控制模式。MCSDK里面默认Id和Iq的PI控制器参数是一样的,下面这个图里面自动生成的参数基本能跑,但是性能没有保障。因而我们需要明白这些参数设置的原理,才能更好的提高电流环控制性能,乃至整个系统的性能。

电流环PI控制器的原理图如下,控制器的输入是电流误差,输出是电压的指令值。需要注意的是,这里的PI是模拟量,PI输出到电压值时需要做模数转换(A/D),采集得到的电流误差值给进PI控制器之前需要做数模转换(D/A),这些转换需要给PI乘上相应的系数,最终体现在PI值上。
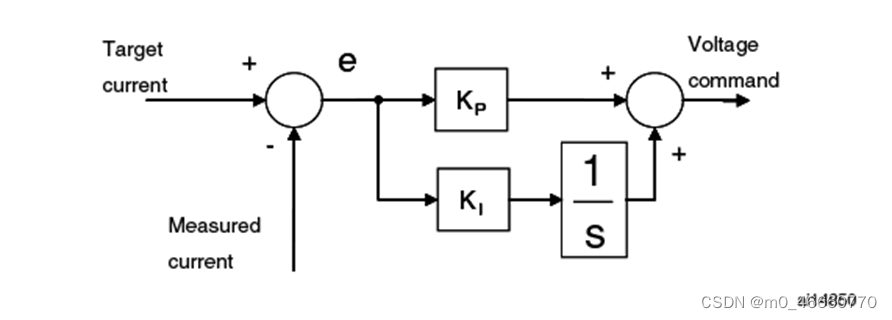
ST电机代码库的电流环PI跟电流环带宽(rad/s)有关,它的表达式如下,

其中,ωc是电流环带宽(rad/s),Rs是定子电阻,Ls是定子电感,Ts是电流环采样时间,Kcv是转换系数。

这个式子中,Rshunt是采样电阻,Aop是运放系数,Vbusdc是母线电压,Vdd是芯片工作电压。
那么回到代码里,
/* Gains values for torque and flux control loops */
#define PID_TORQUE_KP_DEFAULT 2477
#define PID_TORQUE_KI_DEFAULT 3456
#define PID_TORQUE_KD_DEFAULT 100
#define PID_FLUX_KP_DEFAULT 2477
#define PID_FLUX_KI_DEFAULT 3456
#define PID_FLUX_KD_DEFAULT 100
/* Torque/Flux control loop gains dividers*/
#define TF_KPDIV 256
#define TF_KIDIV 8192
#define TF_KDDIV 8192
#define TF_KPDIV_LOG LOG2((256))
#define TF_KIDIV_LOG LOG2((8192))
#define TF_KDDIV_LOG LOG2((8192))我们可以看到设置里不止有PIDKP, PIDKI,还有DIV,这里就涉及到嵌入式的定点数知识了,实际的KP = PID_TORQUE_KP_DEFAULT/ TF_KPDIV,这个设置增大的PI参数的精准度。
感兴趣的朋友可以试着计算一下。























 700
700

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








