《算法从入门到入土系列》第四集博弈论专题

最新推荐文章于 2025-05-03 09:07:35 发布

会划水才能到达彼岸

最新推荐文章于 2025-05-03 09:07:35 发布

阅读量320

点赞数 2

分类专栏：博弈论 Acwing笔记算法系统学习文章标签：博弈论算法

本文链接：https://blog.youkuaiyun.com/m0_46272108/article/details/115712684

版权

Acwing笔记同时被 3 个专栏收录

23 篇文章

订阅专栏

算法系统学习

17 篇文章

订阅专栏

博弈论

1 篇文章

订阅专栏

博弈论本来是数学专题里面的，为什么分一集出来写呢，感觉好久没写博客了，这不得减少点工作量嘛，hhh，其实也不是，其实博弈论里面的东西，挺模板的，很多东西就是离结果只差一点点，还是整理一下好一点吧。

后面还会做一下 kuangbin的题单，给出题解，有兴趣的小伙伴们，可以look一下。

博弈论专有名词及类型

NIM游戏

给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。
所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。
NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

先手必胜：当先手拿完一次，此时的状态为先手必败状态

先手必败：当先手拿完一次，此时的状态为先手必胜状态

定理： NIM博弈先手必胜，当且仅当 $A_1$ ^ $A_2$ ^ … ^ $A_n$ != 0

公平组合游戏ICG

若一个游戏满足：

由两名玩家交替行动；
在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关；
不能行动的玩家判负；
则称该游戏为一个公平组合游戏。
NIM博弈属于公平组合游戏，但城建的棋类游戏，比如围棋，就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不满足条件2和条件3。

有向图游戏

给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。

Mex运算

设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即：
mex(S) = min{x}, x属于自然数，且x不属于S

SG函数

在有向图游戏中，对于每个节点 $x$ ，设从 $x$ 出发共有 $k$ 条有向边，分别到达节点 $y_1, y_2, ..., y_k$ ，定义SG(x)为x的后继节点 $y_1, y_2, ..., y_k$ 的SG函数值构成的集合再执行mex(S)运算的结果，即：
$SG(x) = mex({SG(y_1), SG(y_2), ..., SG(y_k)})$
特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。

有向图游戏的和

设 $G_1, G_2, ..., G_m$ 是m个有向图游戏。定义有向图游戏G，它的行动规则是任选某个有向图游戏 $G_i$ ，并在 $G_i$ 上行动一步。G被称为有向图游戏 $G_1, G_2, ..., G_m$ 的和。
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即：
$SG(G) = SG(G_1)$ ^ $SG(G_2)$ ^ … ^ $SG(G_m)$

定理
有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

NIM游戏

给定N堆物品，第 $i$ 堆物品有 $A_i$ 个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。
所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。

NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

先手必胜：当先手拿完一次，此时的状态为先手必败状态

先手必败：当先手拿完一次，此时的状态为先手必胜状态

定理： NIM博弈先手必胜，当且仅当 $A_1$ ^ $A_2$ ^ … ^ $A_n$ != 0

① $0$ ^ $0$ ^ … ^ $0 = 0$

② $a_1$ ^ $a_2$ ^ … ^ $a_n$ = x ≠ 0

假设 $x$ 的二进制表示中，最高一位1在第k位

$a_1$ ~ $a_n$ 中必然存在一个数 $a_i$ 且满足 $a_i$ 的第k位是1 （反证法：如果从 $a_1$ 到 $a_n$ 中第k位都是0，那么 x 的第k位也必然是0）

$a_i$ ^ $x$ < $a_i$

从物品中拿走 $a_i - (a_i$ ^ $x)$ 个物品

此时变成： $a_i - (a_i -$ $a_i$ ^ $x))$ 即 $a_i$ ^ $x$

所以 $a_1$ ^ $a_2$ ^ $a_3$ ^ … ^ $a_i$ ^ $x$ ^ $a_{i+1}$ ^ … ^ $a_n$ = x ^ x = 0

③ $a_1$ ^ $a_2$ ^ … ^ $a_n$ = 0

证明：不管怎么拿，剩下的异或值一定不为0

反证法：假设其中第 $i$ 堆石子，从 $a_i$ 颗被取成 $a_i'$ 且满足 $a_1$ ^ $a_2$ ^ $a_{i-1}$ ^ $a_i'$ ^ $a_{i+1}$ ^… $a_n$ = 0

那么对这两个式子左右两边同时做异或运算

$a_1$ ^ $a_2$ ^ … ^ $a_n$ = 0

$a_1$ ^ $a_2$ ^ $a_{i-1}$ ^ $a_i'$ ^ $a_{i+1}$ ^… $a_n$ = 0

结果为 $a_i = a_i'$ 与 $a_i' < a_i$ 矛盾，所以当 $a_1$ ^ $a_2$ ^… $a_n$ = 0 不管怎么拿，剩下的异或值一定不为0。

/*

先手必胜状态：可以走到某一个必败状态
先手必败状态：走不到任何一个必败状态

结论：
先手必败：a1^a2^...^an = 0 
先手必胜：a1^a2^...^an != 0

当 如果有两个相等的数 时，例如：
1 1 2 2 3 3 为先手必败态
先手拿完，后手只需要与先手形成镜像拿石子，就能保证，后手一定有石子拿。
那么在这种情况下，^完结果就是0（先手必败）
*/

#include<bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    int n;
    int res = 0;
    cin >> n; 
    while (n--) {
        int x;
        cin >> x;
        res ^= x;
    }
    if (res) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

SG( )函数，如果SG(x) = 0，为必败态
SG(x) != 0，则当前状态一定能到 SG() = 0的状态，所以为必胜态。
LibreOJ 10243.移棋子游戏（SG函数）
在这里插入图片描述

题意：
有向无环图说明能走的完，一定不能有环，有环的话，可以无止境的走下去。图中某些节点可能会有一些棋子，两名玩家交替移动棋子，直到一方无法移动，另一方获胜。

结论：
只有一个棋子的情况下：
先手必胜 <=> 在开始的那个节点的 SG值：SG(start) ≠ 0 即可

多个棋子的情况下：
先手必胜 <=> $sg(s_1)$ ^ $sg(s_2)$ ^ … ^ $sg(s_k) ≠ 0$

实现sg()函数的过程：

sg(u)：看一下u的所有后继节点的sg()值是多少，求完之后可以放到一个set里面去
从小到大枚举每一个自然数，找到第一个不在里面的，然后输出

如果用哈希表的话：
时间复杂度是 O(M+N)

如果用set的话：
时间复杂度是：O(N+MlogM)

LibreOJ 10246. 取石子

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
const int N = 50, M = 50050;
int f[N][M];
int dp(int a, int b) {
    int &v = f[a][b];
    if (v != -1) return v;
    if (!a) return v = b % 2;//b为奇数就是赢，偶数就是输
    //如果b里面只有一堆石子数为1的堆
    if (b == 1) return dp(a + 1, 0);
    
    //a>0才能从a中取，且如果a-1是必败的，则当前状态必胜
    if (a && !dp(a - 1, b)) return v = 1;
    if (b && !dp(a, b - 1)) return v = 1;
    
    //从a中合并2个
    if (a >= 2 && !dp(a - 2, b + (b ? 3 : 2))) return v = 1;
    //a和b中合并一个
    if (a && b && !dp(a - 1, b + 1)) return v = 1;
    return v = 0;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    memset(f, -1, sizeof f);
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        int a = 0, b = 0;
        for (int i = 0; i < n; i++) {
            int x;
            cin >> x;
            if (x == 1) a++;
            //如果b ≠ 0，那么有石子数+x，堆数+1
            //如果b == 0，那么石子数+x，堆数+1，b = 1 + x - 1
            else b += b ? x + 1 : 1 + x - 1;
        }
        if (dp(a, b)) cout << "YES" << endl;
        else cout << "NO" << endl;
    }
    return 0;
}

台阶-Nm博弈 AcWing 892

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    cin >> n; 
    int res = 0;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        if (i & 1) res ^= x;
    }
    if (res) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

博弈论专题刷题

博弈论

HDU 1564（签到题）

在这里插入图片描述
题意：有两个人 “ailyanlu” 和 “8600” ，有个大小是n×n的棋盘。首先，在左上角的格子里放块石头。他们轮流玩，8600先走一步。每一次，玩家都可以水平或垂直地将石头移动到一个未访问的相邻方块上。谁动不了，谁就输。如果双方都采取最优策略，谁将赢得这场比赛?

题解：由于只能移动到为访问的相邻方块上，那么路径就是连续的，所以：
n为奇数，ailyanlu赢
n为偶数，8600赢

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int n;
	while (cin >> n && n) {
		if (n & 1) cout << "ailyanlu" << endl;
		else cout << "8600" << endl;
	}
	return 0;
}

HDU 2516（斐波那契博弈）

在这里插入图片描述
题意：有一堆个数为n的石子，游戏双方轮流取石子，满足：
1)先手不能在第一次把所有的石子取完；
2)之后每次可以取的石子数介于1到对手上一轮取的石子数的2倍之间（包含1和对手刚取的石子数的2倍）。
取走最后一个石子的win

斐波那契数列，f[n]：1,2,3,5,8,13 巧妙猜测：先手胜当且仅当n不是Fibonacci数。换句话说，必败态构成Fibonacci数列。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1000010;
int f[N];
void fib() {
	f[0] = 0;
	f[1] = 1;
	for (int i = 2; i <= N; i++) {
		f[i] = f[i - 1] + f[i - 2]; 
	}
}
signed main()
{
	fib();
	int n;
	while (cin >> n && n) {
		for (int i = 1; i <= N; i++) {
			if (n == f[i]) {
				cout << "Second win" << endl;
				break;
			} else if (n < f[i]) {
				cout << "First win" << endl;
				break;
			}
		}
	}
	return 0;
}

HDU 2897（类巴什博弈）

在这里插入图片描述
题意：给定n,p,q三个数字，总共有n个石子，每轮可以取石子的范围数在：[p, q]
思考的思路：读完题目感觉有点像巴什博弈，巴什博弈的结论是n%(m+1)，每轮可以取石子的范围数是在：[1, m]，所以，判断n%(p+q)>p 一不小心他就可以了，看样例，考虑特殊情况：n%(p+q) == 0 就可以了。

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
	int n, p, q;
	while (cin >> n >> p >> q) {
		int t = n % (p + q);
		if (t > p || t == 0) cout << "WIN" << endl;
		else cout << "LOST" << endl;
	}
	return 0;
}

【2020CCPC网络赛】1005 Lunch （类尼姆博弈）

在这里插入图片描述

2021牛客寒假算法基础集训营3 J.加法和减法

在这里插入图片描述
题解:
如果一开始有偶数张纸牌，其中偶数牌的张数是0或1，那么牛牛有必胜的可能，其他情况下，牛妹有必胜策略。（需要特判一下n==1的情况）

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    int odd = 0, even = 0;
	for (int i = 1; i <= n; i++) {
		int x;
        cin >> x;
		if (x % 2 == 1) odd++;
		else even++;
	}
    if (n == 1) {
        if (odd == 1) cout << "NiuNiu" << endl;
        else cout << "NiuMei" << endl;
        return 0;
    }
	if (n % 2 == 0 && (even == 0 || even == 1)) cout << "NiuNiu" << endl;
    else cout << "NiuMei" << endl;
	return 0;
}

HDU 3389（类阶梯博弈）

在这里插入图片描述

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
    int _;
    scanf("%lld", &_);
    int kase = 0;
    while (_--) {
        int n;
        cin >> n;
        int res = 0;
        for (int i = 1; i <= n; i++) {
            int x;
            cin >> x;
            if (i % 6 == 0 || i % 6 == 2 || i % 6 == 5) res ^= x;
        }
        
        if (res) printf("Case %lld: Alice\n", ++kase);
        else printf("Case %lld: Bob\n", ++kase);
    } 
    return 0;
}

HDU 3863 （签到题）

在这里插入图片描述
读懂题目就可以。
结论：谁先走谁就赢，As Oregon Maple is elder, he will always play first.
Oregon Maple总是先走，就总是他赢

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
	int n;
	while (cin >> n && n != -1) {
		cout << "I bet on Oregon Maple~" << endl;
	} 
	return 0;
}

HDU 3951（环形巴什博弈）

在这里插入图片描述
题解：因为是环形的，如果k==10，给石子标号1~10，假设我要取3颗石子，我可以取第1颗，第2颗和第10颗。先手取完第一次之后，后手只需要按照巴什博弈的规律来操作，就可以保持完胜。
先手胜利的条件：

n为奇数且k=1
k>=n，第一次就能取完所有的石子
其他情况都是后手胜利

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
	int _;
	cin >> _;
	int kase = 0;
	while (_--) {
		int n, k;
		cin >> n >> k;
		cout << "Case " << ++kase << ": ";
		if (n % 2 == 1 && k == 1) cout << "first" << endl;
		else if (n <= k) cout << "first" << endl;
		else cout << "second" << endl;
	} 
	return 0;
}

HDU 2188（标准巴什博弈）

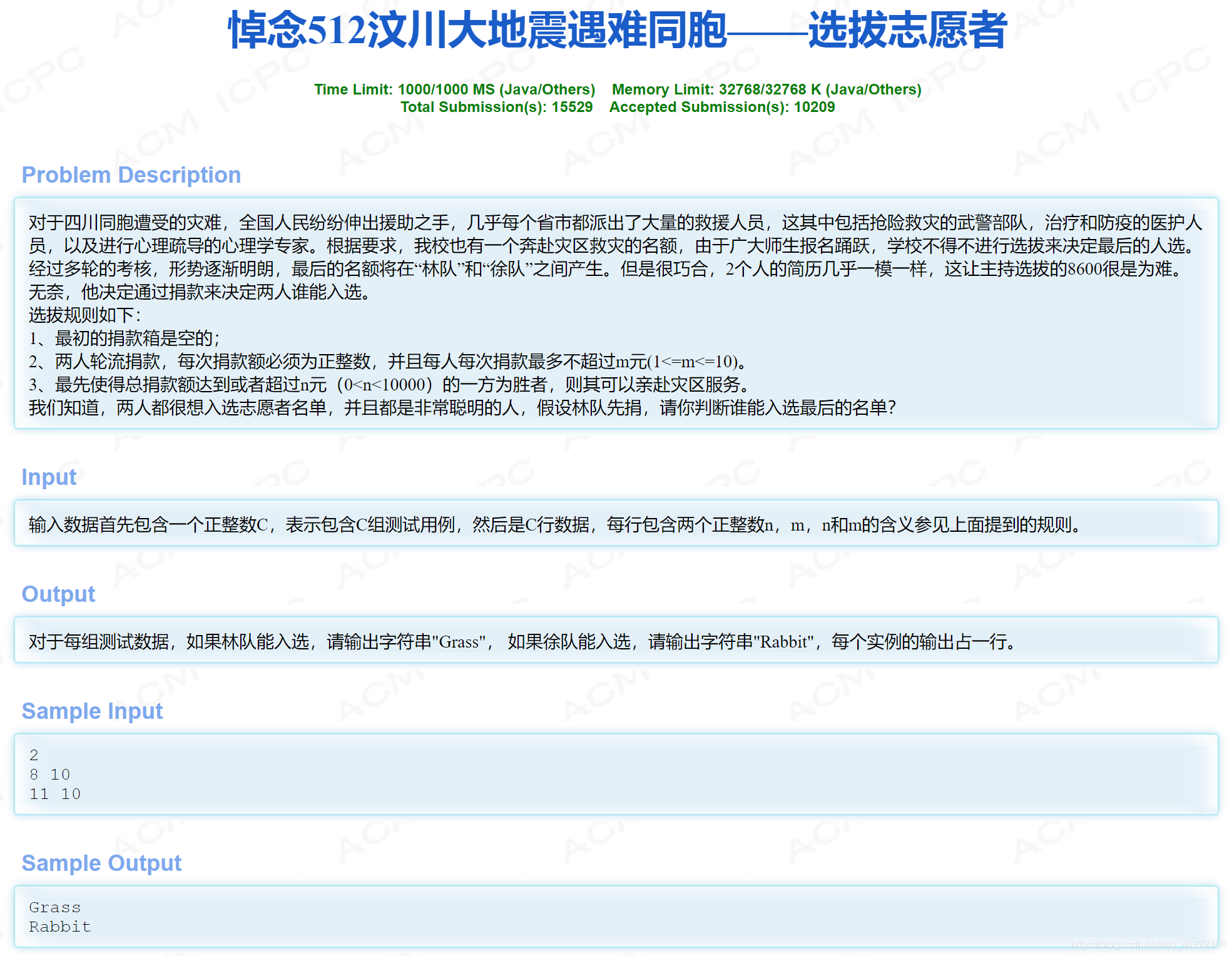
在这里插入图片描述

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
	int _;
	cin >> _;
	while (_--) {
		int n, m;
		cin >> n >> m;
		if (n %(m + 1)) cout << "Grass" << endl;
		else cout << "Rabbit" << endl;
	} 
	return 0;
}

HDU 2149（简单巴什博弈）

在这里插入图片描述

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
	int m, n;
	while (cin >> m >> n && m && n) {
		if (n >= m) {
			for (int i = m; i < n; i++) cout << i << ' ';
			cout << n << endl;
			continue;
		}
		if (m % (n + 1)) cout << m % (n + 1) << endl;
		else cout << "none" << endl;
	} 
	return 0;
}

HDU 2176（尼姆博弈）

在这里插入图片描述
一个标准的尼姆博弈，只是需要输出过程

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 200010;
int a[N];
signed main()
{
	int n;
	while (cin >> n && n) {
		int sum = 0;
		for (int i = 1; i <= n; i++) {
			cin >> a[i];
			sum ^= a[i];
		}
		if (sum) {
			cout << "Yes" << endl; 
			for (int i = 1; i <= n; i++) {
				int t = sum ^ a[i];
                if(t < a[i]) cout << a[i] << ' ' << t << endl;
			}
		}
		else cout << "No" << endl;
	}
	return 0;
}

HDU 1527（威佐夫博弈裸题)

在这里插入图片描述
威佐夫博弈的重要结论

假设两堆石子为(a,b)（其中a<b）

那么先手必败，当且仅当

$(b−a)∗\frac{(\sqrt 5+1)}{2}=a$

其中的 $\frac{(\sqrt 5+1)}{2}$ 实际就是1.618，黄金分割数！

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
	int a, b;
    while (cin >> a >> b) {
    	if (a > b) swap(a, b);
	    int t = abs(a - b);
	    int ans = t * (1.0 + sqrt(5.0)) / 2.0;
	    if (ans == a) cout << 0 << endl;
		else cout << 1 << endl; 
	}
    return 0;
}