GAN系列：李宏毅老师GAN课程P6——Tips for Improving GAN

最新推荐文章于 2022-09-20 23:04:38 发布

burning_planet

最新推荐文章于 2022-09-20 23:04:38 发布

阅读量527

点赞数

CC 4.0 BY-SA版权

分类专栏： Machine Learning Deep Learning

本文链接：https://blog.youkuaiyun.com/lynlindasy/article/details/87902435

Deep Learning 同时被 2 个专栏收录

40 篇文章

订阅专栏

Machine Learning

39 篇文章

订阅专栏

探讨GAN训练中目标函数散度问题，分析图像数据高维特性与采样限制，提出LSGAN与WGAN改进方法，利用Earth Mover's Distance优化生成器，及EBGAN自编码器判别器创新。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在上节课中发现目标函数中的散度会使GAN的训练产生各种各样的问题，通常是因为真实数据分布和生成分布间往往重合部分很少，可从两个方面理解：

1. 图像数据本身的原因：图像表示为一个高维的向量，但在这个高维空间中，只有极少一部分向量是图像(高维空间中的低维流形)。因此在这个高维空间中这两个低维流形的重合是非常少的(低维向量被扭曲成空间)。

2. 在衡量两个分布间的散度时，是先对两个分布采样，由于采样点有限且独立，这两个分布的采样点重合的可能性很小。

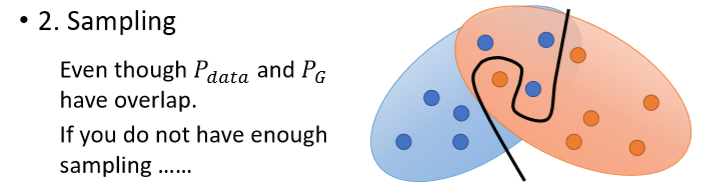
在两个分布几乎不重合的情况下，用JS散度来训练GAN就会产生问题：训练中通过判别器得到两个分布间的散度，然后通过找到最小的散度来得到生成器。但是JS散度有一个特性，两个分布只要不重合，它们之间的JS散度就是log2，如下图所示：

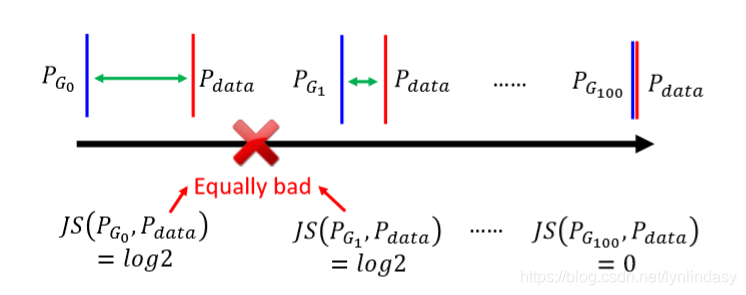
上图中所有的生成分布 $P_{G_0},P_{G_1},...,P_{G_100}$ 等，与真实数据分布 $P_{data}$ 间都是不重合的(由平行线表示)。但从 $P_{G_0}$ 到 $P_{G_1}$ 等等，生成分布越来越靠近真实数据分布 $P_{data}$ ，说明生成器 $G_1$ 优于 $G_0$ ，然而它们与分布 $P_{data}$ 之间的JS散度(由于不重合)都等于log2。在判别器训练后得到这些JS散度后( $JS(P_{G_{0}},P_{data}),JS(P_{G_{1}},P_{data}),...,JS(P_{G_{100}},P_{data})$ )，然而由于它们的值都为log2，生成器无法从 $G_0$ 更新至 $G_1$ (生成器更新的过程是minimize散度，然而所有散度都一样，相当于都是最小值，生成器就不会更新)。这时就相当于一个二分类器(两个分布无重合就相当于两个类别)，只要分类错误，不管这个分类和真实之间的偏差是多少，产生的loss都是固定的。JS这种特性使其不能衡量无重合分布间的距离，生成器无法正常地优化。

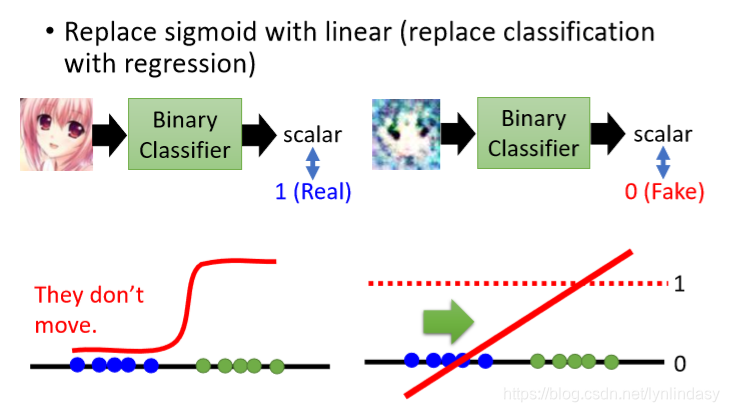
另一种解释方法：此时判别器的输出相当于分类器的输出(如下图所示)，最后的sigmoid函数使得生成分布的采样点(蓝色点)都是非常接近0的值(因为和真实分布不重合，有一定距离)，这部分的梯度非常平缓(sigmoid函数的性质)，类似于梯度消失的概念，训练时优化将十分困难。因此有想法：用线性函数(linear function)代替sigmoid函数，这样分类就转化为了回归(regression)。如果是positive example，令其输出接近1；如果是negative example，令其输出接近0。这就是LSGAN：Least Square GAN。

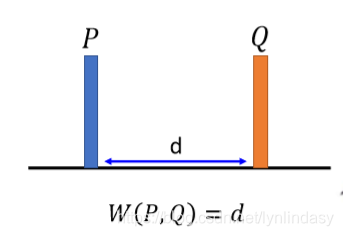
另一种改进方法就是Wasserstein GAN(WGAN)，该方法改变了衡量两个分布间距离的方法，使用Earth Mover's Distance(Wasserstein Distance)。该方法不属于f-divergence，但意义类似。现有两个数据分布P和Q，P视作一堆土，Q视作目标，是另一处的一堆土，把土堆P搬运形成土堆Q要走的平均距离就是Earth Mover's Distance/Wasserstein Distance，如下图所示：这是非常简单的情况，P和Q形式相同，直接把P搬到Q就可以，而且Earth Mover's Distance就是P和Q之间的距离d。

更普遍的情况下，P和Q分布在一定区间(每个分布都是好几堆土构成)，如下图所示，此时把P变成Q存在多种方案(moving plans)：左侧与右侧的方案中所走的平均距离就会不同。此时的Wasserstein Distance就是穷举所有方案(moving plans)，取其中最小值。

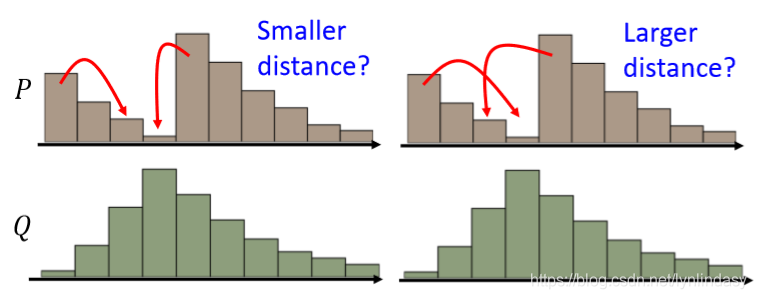
该问题中的最优方案如下图所示：划分出每个小土堆要移动的部分，然后把它们就近挪动，就会得到最短的平均距离。

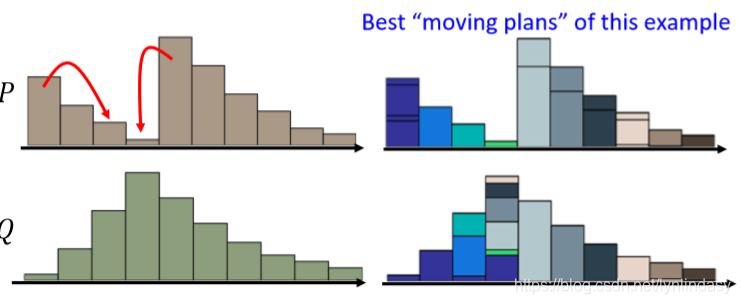
另一种表现形式如下图所示：把一个moving plan化作矩阵 $\gamma$ (所有moving plan的集合写作 $\Pi$ )，其中的每一个元素表示从纵坐标挪到横坐标的量，每一个moving plan( $\gamma$ )的平均距离为 $B(\gamma )=\sum_{x_{p},x_{q}}\gamma (x_{p},x_{q})\left \| x_{p}-x_{q} \right \|$ ，其中 $\gamma (x_{p},x_{q})$ 是矩阵中对应位置元素的值，表示移动的量， $\left \| x_{p}-x_{q} \right \|$ 表示两元素间的距离。则该情况下的Earth Mover's Distance为 $W(P,Q)=\underset{\gamma \in \Pi }{min}B(\gamma )$ ，即平均距离B的最小值。

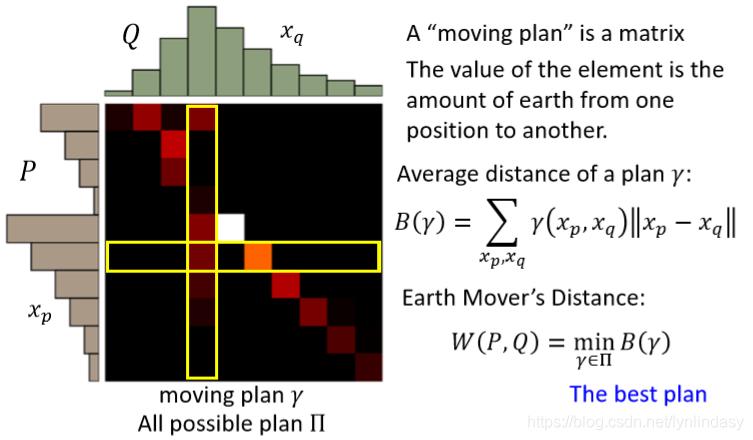
在此意义上，可以发现：每一列的元素值相加就是该列对应的土堆的量，每一行的元素值相加也是该行对应土堆的量。由于涉及到穷举进行minimize，Wasserstein Distance的计算是比较麻烦的，但它可以解决JS散度存在的问题，衡量无重合分布间的真正距离，进而允许生成器优化。

那么该如何修改目标函数，使其可以衡量分布 $P_G$ 和 $P_{data}$ 之间的Wasserstein Distance呢？目标函数 $V(G,D)$ 如下：

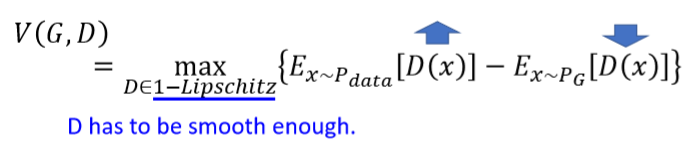
第一项中的 $D(x)$ 是判别器对真实数据的打分，第二项中的 $D(x)$ 是判别器对生成分布的打分，第一项越高越好，第二项则越低越好，表示是一个性能好的判别器。但不对判别器加以限制时，在训练的过程中它将不会收敛(converge)，直到无限大和无限小的值，两者间就会差距极大，导致 $D(x)$ 不平滑，如下图所示：

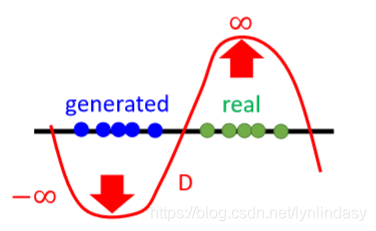
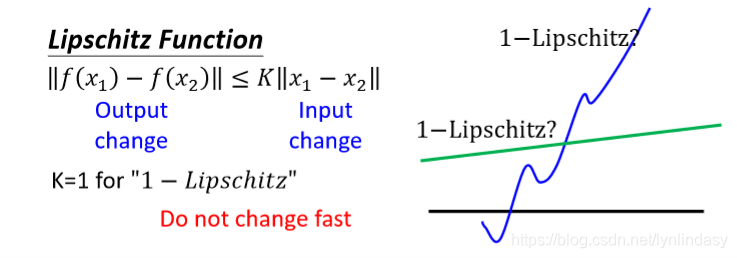
因此需要对其加一个限制(constriant)：1-Lipschitz，令 $D(x)$ 是一个平滑(smooth)的函数。Lipschitz function的定义为：

$\left \| f(x_1)-f(x_2) \right \|\leq K\left \| x_1-x_2 \right \|$ ，其中 $x_1,x_2$ 为函数的输入， $f(x_1),f(x_2)$ 为函数的输出，对于“1-Lipschitz”，K=1。该式就表示，输入的改变缩放一定的倍数后一定不小于输出的变化，说明对输出的改变进行了限制(相当于限制二维中的斜率，在高维中就是对应多个方向导数)，令其不能变化太快，以达到平滑的目的。如下图所示，右图中的蓝线在输入变化很小时输出就跳动很大，导致其不平滑；而绿线就是受限于1-Lipschitz的，是一个平滑函数。

确定目标函数的形式后该如何求解呢：一般情况下max求解利用梯度上升即可，但梯度上升的过程中一般并没有对参数进行限制。此时对梯度上升法进行一定的修改：加入Weight Clipping，限制weight在常数c确定的范围 $[-c,c]$ 内。在梯度上升的过程中观察更新的权重(weight)，若是w>c，则令w=c；若w<-c，令w=-c。但其实并不是利用该方法就能令 $D(x)$ 服从1-Lipschitz，只是会让 $D(x)$ 更平滑一些。

另一种方法是Improved WGAN(WGAN-GP)：一个函数D服从1-Lipschitz等价于D在任意x取值下梯度的范数是不大于1的，即 $D\in 1-Lipschitz\Leftrightarrow \left \| \triangledown _xD(x) \right \|\leq 1$ for all x。令 $D(x)$ 服从1-Lipschitz是比较困难的，但其等价的限制是可以近似得到的：在原本的目标函数后加一项得到： $V(G,D)\approx \underset{D}{max}\left \{ E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[D(x)]-\lambda \int_{x}max(0,\left \| \triangledown _xD(x)- \right \|-1)dx \right \}$ ，加上的这项类似于正则化项(regularization)，对所有x做积分，若是该点的 $||\triangledown _xD(x)||-1>0$ 就会产生penalize。这样在训练过程中就会尽量使得 $\left \| \triangledown _xD(x)\right \|\leq 1$ for all x，但实际上无法对x积分，因为无法sample得到所有的x。因此将正则项改为：

$-\lambda E_{x\sim P_{penalty}}[max(0,\left \|\triangledown _xD(x) \right \|-1)]$ ，假设x服从某个已知分布 $P_{penalty}$ ，这项就表示只要x的采样点服从 $\left \| \triangledown _xD(x)\right \|\leq 1$ 就可以了。此时目标函数为： $V(G,D)\approx \underset{D}{max}\left \{ E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[D(x)]-\lambda E_{x\sim P_{penalty}}[max(0,\left \|\triangledown _xD(x) \right \|-1)] \right \}$ 。

这种方法相当于只对一部分不符合 $\left \| \triangledown _xD(x)\right \|\leq 1$ 的点x进行惩罚，这些被惩罚的点是服从分布 $P_{penalty}$ 的采样点，这个分布表示的区域如下图所示，介于分布 $P_{G}$ 和 $P_{data}$ 之间：

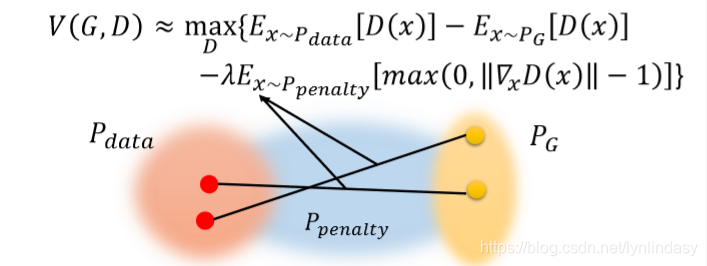
这个分布设置的意义是：只有介于分布 $P_{G}$ 和 $P_{data}$ 之间的点才会有意义，因为分布 $P_{G}$ 在训练中是会不断靠近 $P_{data}$ 的，一定会经过两者之间的部分，中间的点的分布就相当于两者的过渡分布，而空间中其他位置的点几乎不会出现在训练中。 $P_{penalty}$ 是如何确定的呢？从 $P_{data}$ 中sample一个点，从 $P_{G}$ 中sample一个点，两点连直线，从直线上randomly取一个点作为分布 $P_{penalty}$ 中的采样点所以分布 $P_{penalty}$ 就介于两个分布间。继续改进的话，希望梯度范数越接近1越好(上一步中只是希望梯度范数不大于1，只对大于1的点进行惩罚)，对所有梯度范数不等于1的点进行惩罚： $-\lambda E_{x\sim P_{penalty}}[(\left \|\triangledown _xD(x) \right \|-1)^2]$ 。尽管只对大梯度( $\left \| \triangledown _xD(x)\right \|>1$ )的样本点进行penalty也是理论上可行的，但对梯度范数小于1的点也进行penalty能使得算法更快地收敛到更好的局部最优值。

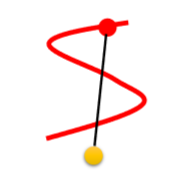
但该方法可能会存在问题：在下图所示的情况中，红色点为分布 $P_{data}$ 中采样点，黄色点为分布 $P_{G}$ 中的采样点，红线表示黄色点能够接近红色点的路径，所以其实只有在该路径上的点才是真正的 $P_{penalty}$ 中的点，求它的梯度才会有意义。也就是黄色点的真实路径并不是黑色的直线，而是红色的曲线，因此对黑色直线采样再求梯度是无意义(don't make sense)的。但红色曲线如何求呢，这是优化的过程，又不是已知的。

这个Wasserstein Distance其实上学期有听过，虽然当时也不是很懂。讲座内容是基于数据的分布式鲁棒优化算法，是一位清华博士分享的，视频链接：https://www.bilibili.com/video/av37311386/。她也是在估计数据的分布中使用了Wasserstein Distance：

1）基于数据的分布未知，想要通过优化目标函数对分布进行估计。目标函数中包含参数 $\xi$ 和决策变量 $x$ ，则一般的优化问题为： $\underset{x\in X}{min} h(x,\xi)$ ；

2）当参数具有不确定性(服从某一分布P，那么参数 $\xi$ 也是一个采样点，具有随机性)时，该优化问题变为： $\underset{x\in X}{min}E_P[h(x,\xi)]$ ，即对包含参数 $\xi$ 的目标函数 $h(x,\xi)$ 求期望；

3）当参数服从的分布P也具有不确定性(在一个分布集合内)，要利用参数的样本 $\left \{ {\xi}_i\right \}_{i=1}^{M}$ 对参数 $\xi$ 服从的分布P进行估计。那么优化问题又变为： $\underset{x\in X}{min}\underset{P\in \mathbb{P}}{max}E_P[h(x,\xi)]$ ，其中 $\mathbb{P}$ 就是根据参数的样本 $\left \{ {\xi}_i\right \}_{i=1}^{M}$ 构造的分布的不确定集。

到此，就是构建了一个分布随机优化问题(所以所谓的分布随机是指参数的分布吧)：既包含了参数的不确定性，也包含了参数分布的不确定性。根据不确定集(参数的分布所在的集合)的形式，鲁棒优化问题可分为几类：

1. 基于矩信息的不确定集： $\mathbb{P}=\left \{ \xi :E[\xi\leq \mu],E[\xi^T\xi]\leq \Sigma ,... \right \}$ ，认为真实分布可以用一阶矩，二阶矩等满足上述条件的集合中。基于矩信息的不确定集的分布随即优化问题一般处理困难，而且也只利用了数据的矩信息，忽略了其他数据能提供的有效信息，且计算比较复杂。

2. 基于概率距离的不确定集： $\mathbb{P}=\left \{P:d(P_m,P)\leq \rho \right \}$ ，认为不确定集是以经验分布 $P_m$ 为中心，半径为?的概率空间一个的球，d(P,Q)是衡量两个分布相似度的一种度量。基于概率距离的不确定集下的分布随机优化问题在选择合适的度量d后，可以将某些无限维的凸分布随机优化问题转化为有限维的凸优化问题。

到这里就引入了Wasserstein Distance， $W(P_1,P_2)=\underset{\gamma \in \Pi (P_1,P_2)}{inf}E_{x,y\sim \gamma }\left \| x-y \right \|$ ，其中 $\Pi(P_1,P_2)$ 代表 $P_1,P_2$ 所有可能联合分布的集合， $x,y$ 就是某个联合分布中的一个采样点，在这个集合下求所有 $x$ 和 $y$ 距离的期望，存在某个联合分布使这个期望最小，这个期望的下确界就是 $P_1,P_2$ 的Wasserstein Distance。

其实一直学到这节课，我才比较理解如何估计一个数据的分布，而度量分布间的距离又是怎样一个概念。感觉GAN这个问题就是个分布随机优化问题的直接应用啊，上面的式子 $\underset{x\in X}{min}\underset{P\in \mathbb{P}}{max}E_P[h(x,\xi)]$ 也就是GAN的目标函数啊。对应一下， $\underset{P\in \mathbb{P}}{max}E_P[h(x,\xi)]$ 是判别器的作用：找到期望最大值(穷举所有参数 $\xi$ 服从的分布看哪一个分布P下得到的目标函数最差)就是在找那些被判别器打了高分的负样本，然后把最大的期望最小化就是生成器根据这些令判别器晕了的负样本对自己进行优化，缩小与真实分布间的距离。

Energy-based GAN(EBGAN)：用一个自编码器(Autoencoder)做判别器，经过编码解码后重建图像，取重建误差(reconstructure error)的负值(图中乘以了-1)，作为判别器的输出。

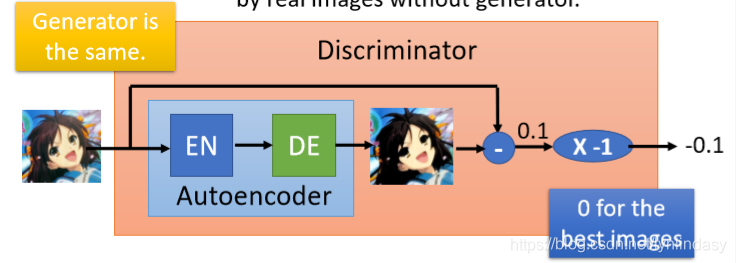
一般的判别器类似一个二分类器，训练它必须需要正负样本，负样本就需要生成器来产生。而一开始，生成器是很差的，产生的负样本也很差，训练得到的判别器就很弱；但EBGAN中判别器是由编码器和解码器组成的，可以仅用真实图像训练，就不需要生成器，因此可以进行预训练，刚开始就有一个很好的判别器。

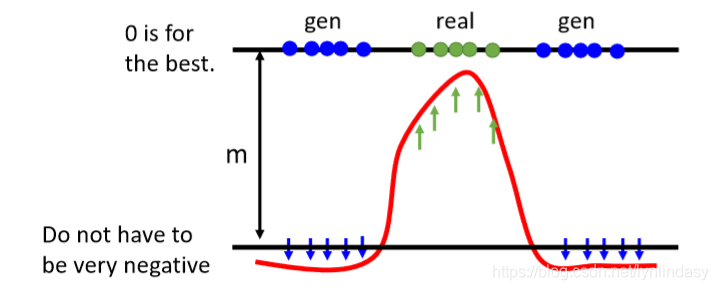
另一方面，在目标函数中，我们一直的标准是让正样本的重建误差尽可能大(因为EBGAN中判别器输出的是负值，所以是越大越好)，让负样本的得分尽可能小。但由于重建是困难的，所以改善重建误差就很难；但产生负样本是简单的，让生成器产生噪声即可。因此这种目标函数在训练中会趋向于不去改进重建误差，而是去减小负样本的得分，使得loss变小(0是最好的情况)，这不是期待的优化方向。因此要给negative example设置一个边界(margin)，限制负样本得分，只要低于margin即可，不需要过低。margin是手调参数。