Work modes recognition and boundary identification of MFR pulse sequences with a hierarchical seq2seq LSTM
期刊信息
IET Radar, Sonar & Navigation
IET Engineering and Technology Journals
Research Article
ISSN 1751-8784
收稿日期:2020年2月2日
修回日期:2020年3月18日
录用日期:2020年4月24日
作者及单位
Yunjie Li¹,², Mengtao Zhu¹,², Yihao Ma¹, Jian Yang²,³
¹School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, People’s Republic of China
²Peng Cheng Laboratory, Shenzhen 518055, People’s Republic of China
³Northern Institute of Electronic Equipment, Beijing 100091, People’s Republic of China
E-mail: liyunjie@bit.edu.cn
阅读论文时的一些问题
为什么不能直接基于脉冲级的h_t进行分类,而是要将h_t再次输入到另一个LSTM中进行分类?
在该论文提出的分层序列到序列长短期记忆(HSSLSTM)框架中,不能直接基于脉冲级bi-LSTM输出的隐藏状态hth_tht进行分类,而需将hth_tht进一步输入片段级bi-LSTM,核心原因在于MFR脉冲序列的分层特性与特征提取需求的匹配性——脉冲级hth_tht仅能捕捉“模式内局部特征”,而片段级LSTM可补充“模式间全局依赖与结构特征”,二者结合才能满足MFR工作模式识别与边界检测的任务要求,具体可从以下三方面结合论文内容展开说明:
1. 脉冲级hth_tht的特征局限性:仅覆盖模式内局部信息
论文明确指出,脉冲级bi-LSTM的核心作用是“提取模式内特征(intra-class features)”。其输出的hth_tht是通过正向(htfh_t^fhtf)与反向(htbh_t^bhtb)遍历原始脉冲序列生成的,本质是单个脉冲在局部上下文(相邻脉冲)中的特征表征。这种特征仅能反映脉冲自身及其近邻脉冲的局部关联(如单个脉冲在某一工作模式内的参数调制规律),但无法捕捉更宏观的“模式间依赖关系”——例如,某一工作模式片段与相邻片段的过渡逻辑、不同模式在序列中的全局分布规律等。而MFR工作模式的本质是“有限或可变数量脉冲组成的片段”,其识别不仅需要判断单个脉冲的局部归属,更需基于片段级的全局结构区分模式类别与检测边界,仅依赖hth_tht的局部特征无法实现这一目标。
2. 片段级LSTM的核心价值:补充模式间全局特征与分层结构匹配性
论文提出HSSLSTM的分层结构,正是为了匹配MFR脉冲序列的“脉冲→片段→模式”分层特性:
- 片段级bi-LSTM以脉冲级特征hth_tht为输入,通过再次正向(h~tf\tilde{h}_t^fh~tf)与反向(h~tb\tilde{h}_t^bh~tb)遍历,专门提取“模式间特征(inter-class features)”——包括不同工作模式片段之间的过渡依赖(如“搜索模式”切换为“跟踪模式”时的序列特征变化)、片段在整个脉冲流中的全局位置信息等;
- 论文强调,这种分层建模与MFR脉冲序列的“天然分层属性一致”,可有效利用序列的层级结构信息。例如,当脉冲序列包含多个模式片段(如“A-B-C-A”)时,片段级LSTM能识别“片段A与片段B的过渡逻辑”,而脉冲级hth_tht仅能感知“A片段内脉冲的局部关联”,无法捕捉跨片段的全局规律。
3. 实验验证:仅用脉冲级hth_tht的模型性能显著不足
论文通过对比“移除片段级LSTM的单层LSTM(SSLSTM)”与完整HSSLSTM的性能,直接验证了片段级LSTM的必要性。实验结果显示,在复杂非理想场景(如含30%丢失脉冲、60%杂波脉冲的混合场景4-7)中,HSSLSTM的识别准确率显著优于SSLSTM。这一差异的核心原因在于:SSLSTM仅依赖脉冲级hth_tht进行分类,缺乏对模式间全局依赖的建模,面对多片段、高污染的长序列时,易因“局部特征误判”导致边界检测错误或类别混淆;而HSSLSTM通过片段级LSTM补充全局结构特征,可有效规避这一问题。
综上,直接基于脉冲级hth_tht分类无法覆盖MFR脉冲序列的全局结构与模式间依赖,与论文“分层建模匹配MFR序列特性、联合提取 intra/inter 特征”的核心设计思想相悖;而将hth_tht输入片段级LSTM,是实现“精准识别多模式类别+检测过渡边界”任务目标的关键设计,且实验已验证该分层结构的优越性。
摘要
识别输入脉冲序列中的多功能雷达(MFR)工作模式,是解析MFR功能与行为的基础任务。该任务需解决三大核心挑战:(1)接收的雷达脉冲流可能包含数量未知的多段工作模式类别片段;(2)现代MFR的模式内与模式间特性灵活复杂,难以通过传统手工特征与学习模型进行表征和学习;(3)各工作模式的持续时长不固定,导致相邻模式的过渡边界难以检测。为应对上述挑战并实现脉冲级MFR工作模式序列的自动识别,本文基于MFR工作模式序列的时间序列表征与序列到序列(seq2seq)长短期记忆网络,提出一种新型处理框架。该方法不仅能自动识别脉冲序列中多类复杂调制的工作模式,还能通过为每个脉冲标注类别信息,精准检测各类别间的过渡边界。实验结果表明,相较于当前主流的工作模式分类方法,所提方法具备更全面的功能与更优的性能。
1 引言
在认知电子侦察系统中,精准理解雷达意图具有重要作用[1]。随着电扫描相控阵技术的发展,现代多功能雷达(MFR)能够同时执行多项任务,且具备高度智能性、灵活性与适应性[2-5]。每种特定任务的调制模式在脉冲重复间隔(PRI)、脉冲宽度(PW)和射频(RF)等参数上均表现出显著差异性[6,7]。因此,精准识别、分析与预测MFR工作模式成为一项艰巨挑战,但目前该领域的研究仍相对有限。
早期模式识别技术(如模板匹配[8,9]、统计直方图法[10])在工作模式由固定调制参数定义的传统雷达中表现良好,但无法对MFR的动态变化行为进行建模与识别。因此,亟需建立新的表征模型与处理框架,用于分析MFR的行为特性。
首先,Visnevski[11]提出一种分层模型来描述MFR的灵活性与动态性:将雷达行为划分为“雷达字”(word)、“雷达指令”(即工作模式)和“任务”三个层级。其中,“雷达字”表示有限个脉冲的固定排列,“雷达工作模式”表示有限个雷达字的串联。因此,执行特定雷达任务的调度型工作模式序列可通过句法方式描述。该研究中提出的MFR信号分层模型与句法建模方法,已被广泛应用于各类MFR工作模式相关研究[7,12-21]。
此后,众多基于分层模型的工作模式识别方法被提出。这些方法通常先从输入脉冲流中提取“雷达字序列”,再执行识别任务[15,16,18-20]。此类两阶段识别方法在“水星”(Mercury)、“冥王星”(Pluto)等早期MFR中表现良好[11],但面对新型MFR时性能会显著下降,主要原因包括:(1)这类方法需要各层级中所有基本元素及其过渡规则的充足先验信息,而实际应用中往往无法获取完整先验;(2)它们将所有可用先验知识编码为近乎固定的拟合模型,并在该先验框架下分析截获信号。然而,实际截获的雷达信号可能包含杂波脉冲、丢失脉冲与测量误差脉冲,导致基于先验的模板失效,甚至无法处理PRI、RF、PW等参数动态捷变的工作模式[6,7,22]。
随后,研究发现脉冲间参数(PRI、RF、PW)的调制模式是区分不同工作模式的固有特征,这为解析MFR工作意图提供了可行方向[23]。借助机器学习分类器,学者们设计了多种脉冲间调制分类方法以应对现代MFR的识别问题[23-28]。例如,文献[23]设计了不变特征与分层分类方案,用于对MFR辐射源的复杂PRI调制模式进行分类;近年来,基于深度学习网络的自动特征提取方法被用于高污染场景下的PRI调制分类[27],该研究采用一维卷积神经网络(1-D CNN)并取得了理想性能;此外,Liu与Yu[28]利用循环神经网络(RNN)对不同周期时长的脉冲序列进行分类,克服了卷积神经网络(CNN)对输入长度固定的限制。
上述所有研究均采用“序列到单一输出”(seq2one)的直接粗粒度识别方案:输入一个脉冲序列,仅输出该序列整体的单一类别标签。然而,现代MFR的脉冲信号通常以连续脉冲流形式存在。在非协作场景下,难以将截获的脉冲序列完美分段,因此seq2one方法无法对多类别混合的输入序列进行正确分类,且其部分正确的结果粒度过粗,无法支撑后续深入分析。
为缓解基础seq2one分类器的上述缺陷,文献[23]提出滑动窗口技术:通过设置合适的窗口长度,可识别序列中存在的多类别并检测相邻类别的边界,但需付出一定计算开销。然而,滑动窗口内每次分类操作仍基于seq2one方案,不仅分类结果粒度粗,还无法利用序列中不同工作模式间的依赖关系与类间特征,因此在实际应用中性能难以满足需求。
序列到序列(seq2seq)方法可克服seq2one方案的局限性。理想的seq2seq分类器应能接收输入脉冲序列,并为每个脉冲生成一个模式标签,最终形成输出标签序列。一旦获取每个脉冲的类别标签,即可精准确定序列中包含的多类别及其过渡边界。基础seq2seq方法及其变体已在神经机器翻译[29,30]、序列标注[31]、文档分析[32]、图像描述[33]等领域广泛应用;近年来,该方法还被用于脑电信号标记[34]、轨迹规划[35]、电能质量扰动识别[36]等领域。然而,据作者所知,目前尚无研究将seq2seq方法应用于MFR工作模式序列分析。
本文提出一种基于分层序列到序列长短期记忆网络(HSSLSTM)的新型框架,实现脉冲级MFR工作模式序列的自动识别。通过精心设计的序列制备与固定阈值归一化处理,经有效模型训练后,该方法不仅能自动识别脉冲序列中所有复杂调制的工作模式类别,还能通过为每个脉冲标注类别信息,精准检测各类别的边界。脉冲级模式标注能力还可实现杂波脉冲的自动标记与截获信号的后续深入分析。该方法克服了基于seq2one方案与滑动窗口技术的传统方法在上下文利用、分类粒度、计算开销与性能稳定性方面的不足,并通过全面实验验证了其有效性与鲁棒性。
本文的主要贡献如下:
(1)设计了MFR工作模式序列的新型时间序列表征方式;
(2)提出了基于HSSLSTM的脉冲级MFR工作模式识别框架;
(3)所提框架可精准识别脉冲序列中包含的多类工作模式,并检测所有类别间的过渡边界;
(4)脉冲级识别结果可实现杂波脉冲的自动标记与后续细粒度分析。
全文结构安排如下:第2章阐述脉冲级MFR工作模式序列识别任务的数学建模;第3章介绍所提框架的整体结构及三个处理步骤的实现细节;第4章提供数据描述、实验设计与实验结果;第5章总结全文并给出未来研究方向。
2 问题建模
本文旨在实现连续输入MFR工作模式序列的脉冲粒度自动识别。本章将介绍典型MFR工作模式、定义工作模式序列,并给出识别任务的数学建模。
2.1 候选MFR工作模式定义
为满足不同功能任务的性能需求,MFR需优化脉冲内与脉冲间参数,并在时间轴上调度工作模式[2-5,37-40]。MFR工作模式可定义为执行特定雷达功能的有限或可变数量脉冲的排列。本文参考文献[22,23],将MFR工作模式定义为PRI、RF、PW三参数脉冲间调制模式的组合。具体而言,脉冲间调制类型相同但调制参数不同的脉冲序列,视为同一工作模式;相邻脉冲片段间调制类型的变化,通常表明MFR发生模式过渡。
上述三个参数存在不同的脉冲间调制类型:对于PRI调制,文献[23]提出6类典型模式,包括固定PRI、捷变PRI、抖动PRI、驻留切换PRI、滑动PRI与周期PRI;RF与PW参数也可采用这些典型调制模式。为不失一般性,本文人工定义5类MFR工作模式作为候选类别,如表1所示。需说明的是,第4类模式包含两个等概率子模式,这是考虑到MFR的特定工作模式可能存在子模式(例如,文献[41]中描述的“搜索模式”包含针对不同机动目标的“近程搜索”与“远程搜索”两个子模式)。
表1 基于PRI、RF和PW调制模式的5种典型MFR工作模式定义
| 工作模式类别 | PRI调制模式 | RF调制模式 | PW调制模式 |
|---|---|---|---|
| 1 | 驻留切换 | 固定 | 固定 |
| 2 | 捷变 | 捷变 | 捷变 |
| 3 | 抖动 | 抖动 | 固定 |
| 4 | 驻留切换 | 驻留切换/固定 | 捷变 |
| 5 | 滑动 | 驻留切换/固定 | - |
2.2 MFR工作模式序列的分层定义
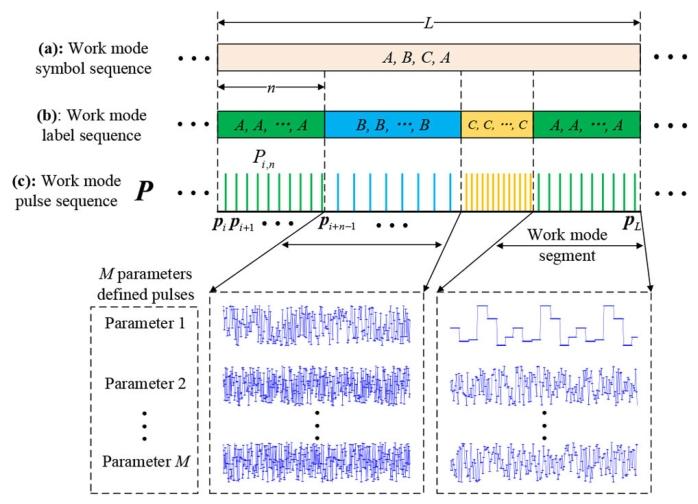
参考传统脉冲多普勒MFR的分层结构[13]与序列基本元素定义[42],本文将MFR工作模式序列定义为多层架构。图1展示了基于M个参数的MFR工作模式序列示意图。
图1 基于M个参数的雷达工作模式序列示意图(自上而下)
(a)工作模式符号序列:描述脉冲序列P中各片段的片段级标签;(b)工作模式标签序列:描述脉冲序列P中每个脉冲的脉冲级标签;(c)工作模式脉冲序列P:包含构成多工作模式片段的所有脉冲,每个片段由子序列构成,每个脉冲由M维参数向量表示。
定义1:雷达脉冲p∈RMp \in \mathbb{R}^{M}p∈RM用M维实值向量表示,即p=(p1,p2,...,pM)Tp=(p_{1}, p_{2}, ..., p_{M})^{T}p=(p1,p2,...,pM)T。
定义2:包含L个脉冲的(工作模式)脉冲序列P∈RM×LP \in \mathbb{R}^{M \times L}P∈RM×L,是有序脉冲的集合。
定义3:脉冲序列P中包含n个脉冲的(工作模式)片段Pi,n∈RM×nP_{i,n} \in \mathbb{R}^{M \times n}Pi,n∈RM×n,是脉冲子序列Pi,n=(pi,pi+1,...,pi+n−1)P_{i,n}=(p_{i}, p_{i+1}, ..., p_{i+n-1})Pi,n=(pi,pi+1,...,pi+n−1),其中1≤i≤L−n+11 \leq i \leq L-n+11≤i≤L−n+1且n≤Ln \leq Ln≤L。每个片段属于某一类别,不同片段可属于同一类别。
定义4:包含J个工作模式片段与K个工作模式类别的(工作模式)符号序列,是存储工作模式类别符号的数据结构,其中每个符号代表P中一个片段的工作模式类别。例如,符号序列为“A, B, C, A”的脉冲序列P,包含4个连续片段,分属3个类别。
定义5:脉冲序列P的(工作模式)标签序列,是存储P中每个雷达脉冲工作模式类别标签的数据结构(每个脉冲对应一个标签)。需注意,同一片段Pi,nP_{i,n}Pi,n中的所有脉冲可能不属于同一类别(例如,多辐射源信号解交织不完全时,会导致部分杂波脉冲混入P,且这些杂波脉冲与片段中其他脉冲不属于同一类别)。
为简化表述,后续章节中括号内的“工作模式”一词将酌情省略。
2.3 脉冲级MFR工作模式识别任务
脉冲级MFR工作模式识别任务要求为输入测试脉冲序列输出一个标签序列(每个脉冲对应一个标签)。设包含L个脉冲的输入脉冲序列为P=(p1,p2,...,pL)P=(p_{1}, p_{2}, ..., p_{L})P=(p1,p2,...,pL),其中pt=(pt1,pt2,...,ptM)p_{t}=(p_{t1}, p_{t2}, ..., p_{tM})pt=(pt1,pt2,...,ptM)(1≤t≤L1 \leq t \leq L1≤t≤L)表示第t个脉冲;P对应的真实标签序列为Y=(y1,y2,...,yL)Y=(y_{1}, y_{2}, ..., y_{L})Y=(y1,y2,...,yL)。脉冲级识别的目标是为P计算预测标签序列Y^=(y^1,y^2,...,y^L)\hat{Y}=(\hat{y}_{1}, \hat{y}_{2}, ..., \hat{y}_{L})Y^=(y^1,y^2,...,y^L)(每个脉冲对应一个预测标签)。
文献[27,28]中的“seq2one”方法仅考虑静态场景:假设预分段的测试脉冲序列P仅包含“纯净”数据且属于单一类别。然而,雷达脉冲以流形式存在,在复杂电磁环境中难以保证上述理想场景,截获的脉冲序列P中可能包含多类工作模式(如图2所示)。一个可靠的脉冲级识别方案需妥善解决以下三大挑战:(1)输入测试脉冲序列P通常包含多个分属不同工作模式类别的片段,且片段数量与类别数量随样本变化;(2)不同类别或不同样本中,片段包含的脉冲数量存在差异;(3)由于截获处理限制,P首尾两端的片段可能被截断,导致工作模式模式不完整。
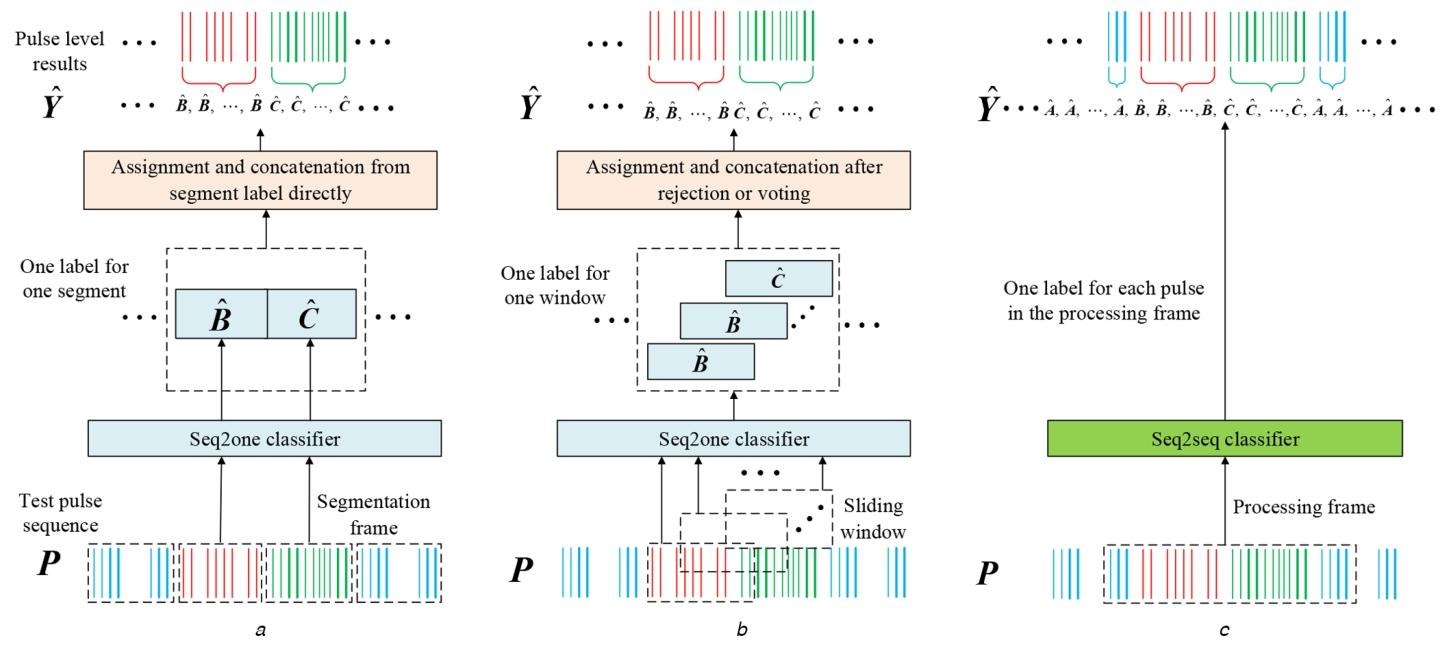
图2 传统seq2one方案与seq2seq方案用于脉冲级识别的示意图
(a)基于专属分段的seq2one分类;(b)基于滑动窗口的seq2one分类;(c)用于脉冲级工作模式识别的seq2seq方案。
为应对上述挑战并实现脉冲级识别,部分专属分段方法首先将整个序列划分为多个非重叠片段,为每个片段预测一个标签(如图2a),再将片段标签分配给该片段内所有脉冲,最终拼接所有标签形成脉冲级结果。然而,在缺乏充足先验信息的情况下,难以实现片段的精准划分,导致这类“分段-分类”方法存在大量分类误差。
随后,文献[23]采用滑动窗口技术实现自适应划分与脉冲级分类(如图2b):按用户定义的步长滑动窗口,以seq2one方式为每个窗口内的脉冲序列分类;通过拼接所有窗口的分类结果形成最终输出。对于被多个窗口覆盖的脉冲,有两种处理方式:一是采用文献[23]的方法,通过经验阈值剔除模式过渡区域窗口的分类结果;二是对多个重叠窗口的分类结果进行投票,将得票最高的标签分配给重叠脉冲。尽管上述两种方法可借助滑动窗口获取脉冲级预测结果,但其核心仍基于seq2one分类,因此实际精度粒度仍为片段级。
seq2seq方法是实现脉冲级识别任务的直观且可行的方案。图2c展示了seq2seq方案用于脉冲级工作模式识别的映射关系:训练良好的seq2seq模型可联合挖掘整个输入脉冲序列的模式内与模式间特征,而非像文献[23]那样拼接多个seq2one识别结果,从而确定每个脉冲的类别标签。
3 方法设计
3.1 所提脉冲级识别框架
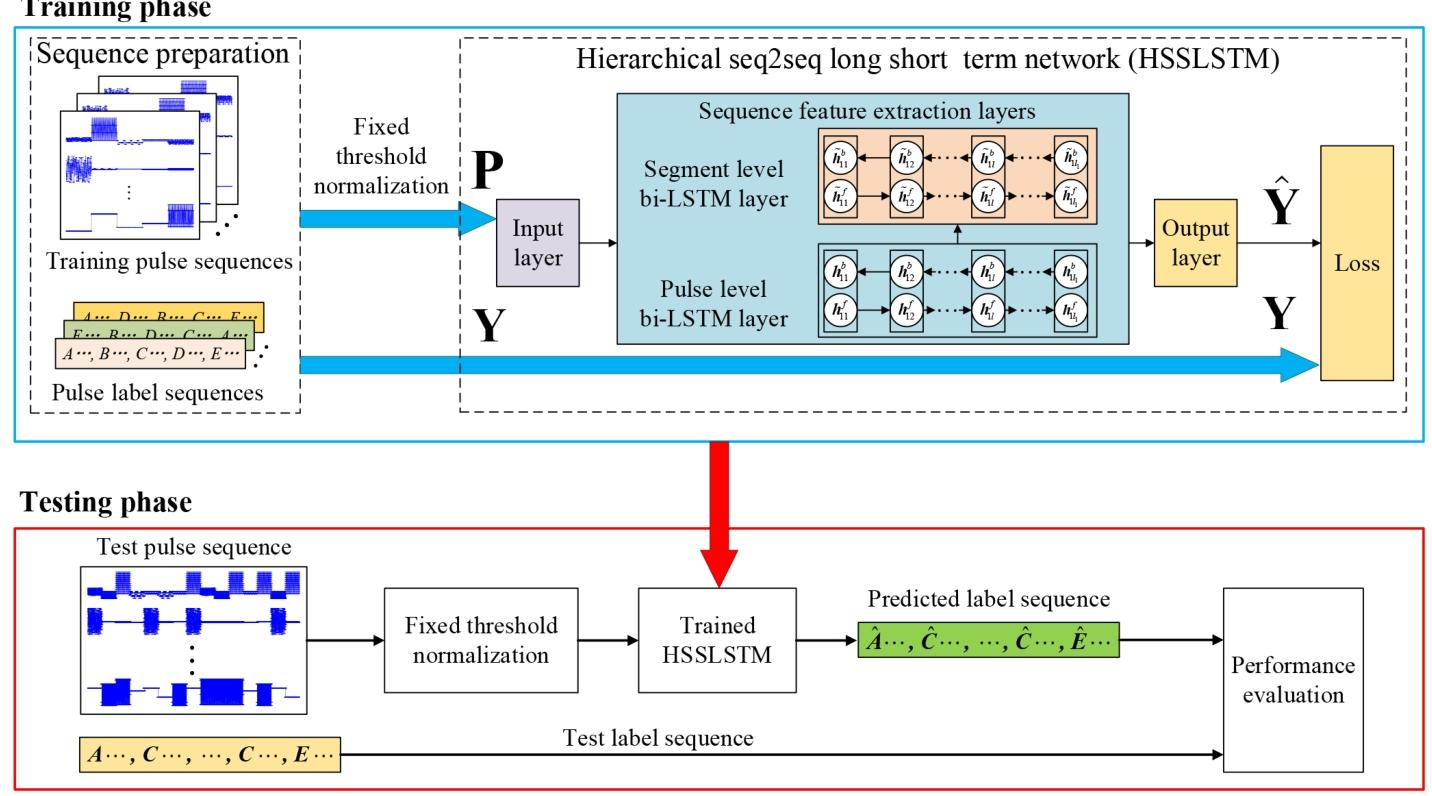
为克服seq2one方法在脉冲级识别中的缺陷,本文提出一种新型seq2seq处理框架,其流程图如图3所示。
图3 基于seq2seq的脉冲级工作模式识别框架流程图
所提框架的训练过程包含三个核心步骤:(1)序列制备:生成训练数据;(2)固定阈值归一化:保障模型有效训练;(3)HSSLSTM构建:实现脉冲级识别。
3.2 序列制备
首先分析典型MFR模式序列的特性:以“搜索”(模式“A”)、“跟踪”(模式“B”)、“测距”(模式“C”)三类典型工作模式为例,“搜索”模式可能持续一段时间(如符号序列“A, A, A”);当跟踪目标丢失时,MFR会从“跟踪”模式切换回“搜索”模式,导致符号序列出现模式过渡(如“A, B, C, A”);此外,“测距”等模式仅在需要识别目标时短暂出现(如符号序列“A, B, C, A”中“C”仅出现一次,而在“A, A, A, B”中未出现)。
考虑到上述场景,需通过序列制备步骤生成高质量训练数据,以确保模型在复杂实际场景中仍能有效训练并取得理想识别性能(实际场景中,序列可能包含任意数量的已知类别,每个类别包含任意数量的片段,且不同样本中类别对应的脉冲数量动态变化)。为保证模型能充分学习模式内与模式间特征,训练样本需覆盖所有可能类别及所有可能类别顺序,因此需根据具体识别任务精心设计训练样本。
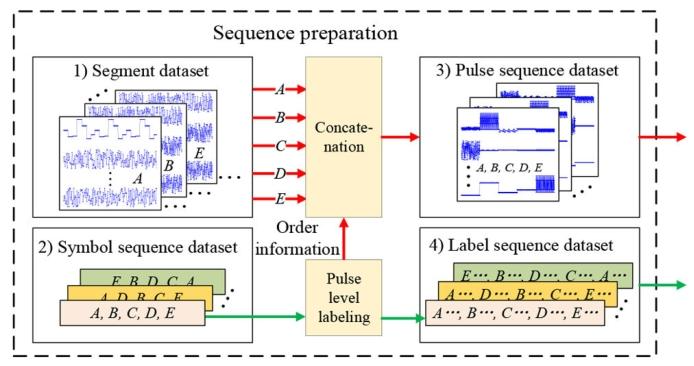
所提框架的序列制备步骤包含四个连续子步骤:(1)片段数据集生成;(2)符号序列数据集生成;(3)脉冲序列数据集生成;(4)标签序列数据集生成,具体流程如图4所示。
图4 序列制备流程
红色线条表示生成包含“A, B, C, D, E”片段的脉冲序列的步骤;绿色线条表示生成标签序列的步骤。
(1)片段数据集生成:为每个工作模式类别独立仿真样本,每个样本仅包含单一工作模式类别,且不同样本的脉冲数量与调制参数存在差异。
(2)符号序列数据集生成:每个符号序列样本包含K个来自K个类别的工作模式符号(每个符号对应一个类别),符号顺序随机生成,以覆盖所有可能的序列场景。
(3)脉冲序列数据集生成:将符号序列数据集中每个样本的每个符号,替换为片段数据集中对应的片段,从而拼接形成脉冲序列数据集。例如,图4中符号序列“A, B, C, D, E”(分属5个工作模式类别),通过拼接片段数据集中对应的5个片段样本,转化为脉冲序列。
(4)标签序列数据集生成:根据符号序列数据集与脉冲序列数据集生成标签序列数据集,为脉冲序列中的每个脉冲标注对应类别标签。此外,借助标签级识别能力,可将脉冲序列中的所有杂波脉冲标注为新类别(即第K+1类)。
3.3 固定阈值归一化
脉冲通常由多个参数(本文为M个)表征,这些参数的单位与数量级不同,因此需通过归一化将其转换为可比尺度。传统归一化方法基于序列中参数的最大值与最小值对参数向量aaa进行归一化。
然而,在脉冲级MFR工作模式识别问题中,序列可能不包含所有模式类别。若仅基于序列中已存在类别的参数进行归一化,会破坏类别间的相对关系,导致分类误差;在测试阶段,由于无法保证接收的测试序列在给定时间内包含所有模式类别,这种误差会进一步扩大。
为此,本文基于M个参数的固定下界LB=[LB1,LB2,...,LBM]LB=[LB_1, LB_2, ..., LB_M]LB=[LB1,LB2,...,LBM]与上界UB=[UB1,UB2,...,UBM]UB=[UB_1, UB_2, ..., UB_M]UB=[UB1,UB2,...,UBM],采用下述公式对脉冲序列进行归一化:
am′=2(am−LBm)UBm−LBm−1,m=1,2,...,Ma_{m}'=\frac{2\left(a_{m}-LB_{m}\right)}{UB_{m}-LB_{m}}-1, \quad m=1,2, ..., Mam′=UBm−LBm2(am−LBm)−1,m=1,2,...,M
其中,ama_mam为输入序列的第m个参数向量,通过对应的下界LBmLB_mLBm与上界UBmUB_mUBm进行归一化;LBLBLB与UBUBUB的取值可依据脉冲参数的统计区间确定。该方法可避免因类别缺失导致的归一化过程中类别间关系破坏的问题。
3.4 用于脉冲级识别的HSSLSTM构建
长短期记忆网络(LSTM)[43]及其变体[44,45]已在脉冲序列分类[28]等众多领域广泛应用。为同时学习模式内与模式间特征,所提框架采用基于分层seq2seq的双向LSTM(bi-LSTM)网络,该分层结构与MFR脉冲序列的分层特性一致,有利于提升识别性能。
3.4.1 HSSLSTM网络结构
所提bi-LSTM网络包含两个层级的bi-LSTM层:脉冲级bi-LSTM层与片段级bi-LSTM层,分别用于提取模式内特征与模式间特征。
经归一化后,得到包含N个脉冲序列样本的训练数据集D={P1,Y1;P2,Y2;...;PN,YN}D=\{P_1,Y_1; P_2,Y_2; ...; P_N,Y_N\}D={P1,Y1;P2,Y2;...;PN,YN},其中:
- Pi=(Pi1,Pi2,...,PiJ)P_i=(P_{i1}, P_{i2}, ..., P_{iJ})Pi=(Pi1,Pi2,...,PiJ)为第i个样本,Pij=(pij1,pij2,...,pijlj)P_{ij}=(p_{ij1}, p_{ij2}, ..., p_{ijl_j})Pij=(pij1,pij2,...,pijlj)(1≤j≤J1 \leq j \leq J1≤j≤J)为第i个样本的第j个片段;
- J=KJ=KJ=K(K为总类别数,即第i个样本的片段数);
- ljl_jlj为第j个片段的脉冲数,因此第i个样本的总脉冲数为Li=∑j=1KljL_i=\sum_{j=1}^{K} l_jLi=∑j=1Klj;
- 每个脉冲p=(p1,p2,...,pM)Tp=(p_1, p_2, ..., p_M)^Tp=(p1,p2,...,pM)T由M个参数表征,故Pi∈RM×LiP_i \in \mathbb{R}^{M \times L_i}Pi∈RM×Li;
- Yi=(yi1,yi2,...,yiLi)Y_i=(y_{i1}, y_{i2}, ..., y_{iL_i})Yi=(yi1,yi2,...,yiLi)为PiP_iPi对应的标签序列。
将数据集D输入HSSLSTM网络进行训练。
3.4.2 脉冲级bi-LSTM层
脉冲级bi-LSTM层沿正向(以上标“f”表示)与反向(以上标“b”表示)两个方向遍历原始脉冲序列PiP_iPi,分别生成隐藏状态向量Hif=(hi1f,hi2f,...,hiLif)H_i^f=(h_{i1}^f, h_{i2}^f, ..., h_{iL_i}^f)Hif=(hi1f,hi2f,...,hiLif)与Hib=(hi1b,hi2b,...,hiLib)H_i^b=(h_{i1}^b, h_{i2}^b, ..., h_{iL_i}^b)Hib=(hi1b,hi2b,...,hiLib),其中:
hitf=LSTM(pit,hi(t−1)f),t=1,2,...,Lih_{it}^f = \text{LSTM}(p_{it}, h_{i(t-1)}^f), \quad t=1,2, ..., L_ihitf=LSTM(pit,hi(t−1)f),t=1,2,...,Li
hitb=LSTM(pit,hi(t+1)b),t=Li,Li−1,...,1(3)h_{it}^b = \text{LSTM}(p_{it}, h_{i(t+1)}^b), \quad t=L_i, L_i-1, ..., 1 \tag{3}hitb=LSTM(pit,hi(t+1)b),t=Li,Li−1,...,1(3)
式中,pitp_{it}pit为第i个样本的第t个脉冲(时间步t);LSTM(⋅)\text{LSTM}(\cdot)LSTM(⋅)表示LSTM单元函数,由以下公式实现:
ft=σ(Wf⋅[ht−1,xt]+bf)f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)ft=σ(Wf⋅[ht−1,xt]+bf)
it=σ(Wi⋅[ht−1,xt]+bi)i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)it=σ(Wi⋅[ht−1,xt]+bi)
C~t=tanh(WC⋅[ht−1,xt]+bC)\tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)C~t=tanh(WC⋅[ht−1,xt]+bC)
Ct=ft⊙Ct−1+it⊙C~tC_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_tCt=ft⊙Ct−1+it⊙C~t
ot=σ(Wo⋅[ht−1,xt]+bo)(12)o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \tag{12}ot=σ(Wo⋅[ht−1,xt]+bo)(12)
ht=ot⊙tanh(Ct)h_t = o_t \odot \tanh(C_t)ht=ot⊙tanh(Ct)
其中,ftf_tft、iti_tit、oto_tot与C~t\tilde{C}_tC~t分别表示遗忘门向量、输入门向量、输出门向量与候选细胞状态向量;带下标与门标识的WWW和bbb分别表示对应门的权重矩阵与偏置向量;CtC_tCt为细胞状态;⊙\odot⊙表示元素-wise乘法;σ(⋅)\sigma(\cdot)σ(⋅)与tanh(⋅)\tanh(\cdot)tanh(⋅)分别为sigmoid激活函数与双曲正切激活函数。
将正向与反向隐藏状态向量拼接,即hit=[hitf,hitb]h_{it}=[h_{it}^f, h_{it}^b]hit=[hitf,hitb],得到脉冲pitp_{it}pit的脉冲级特征表征。关于LSTM单元的详细信息,可参考文献[43,45]。
3.4.3 片段级bi-LSTM层
片段级bi-LSTM层遍历脉冲级bi-LSTM层生成的隐藏状态向量Hi=(hi1,hi2,...,hiLi)H_i=(h_{i1}, h_{i2}, ..., h_{iL_i})Hi=(hi1,hi2,...,hiLi),分别生成正向与反向的片段级隐藏状态向量H~if=(h~i1f,h~i2f,...,h~iLif)\tilde{H}_i^f=(\tilde{h}_{i1}^f, \tilde{h}_{i2}^f, ..., \tilde{h}_{iL_i}^f)H~if=(h~i1f,h~i2f,...,h~iLif)与H~ib=(h~i1b,h~i2b,...,h~iLib)\tilde{H}_i^b=(\tilde{h}_{i1}^b, \tilde{h}_{i2}^b, ..., \tilde{h}_{iL_i}^b)H~ib=(h~i1b,h~i2b,...,h~iLib),其中:
h~itf=LSTM(hit,h~i(t−1)f),t=1,2,...,Li(10)\tilde{h}_{it}^f = \text{LSTM}(h_{it}, \tilde{h}_{i(t-1)}^f), \quad t=1,2, ..., L_i \tag{10}h~itf=LSTM(hit,h~i(t−1)f),t=1,2,...,Li(10)
h~itb=LSTM(hit,h~i(t+1)b),t=Li,Li−1,...,1(11)\tilde{h}_{it}^b = \text{LSTM}(h_{it}, \tilde{h}_{i(t+1)}^b), \quad t=L_i, L_i-1, ..., 1 \tag{11}h~itb=LSTM(hit,h~i(t+1)b),t=Li,Li−1,...,1(11)
同样,将正向与反向片段级隐藏状态向量拼接,即h~it=[h~itf,h~itb]\tilde{h}_{it}=[\tilde{h}_{it}^f, \tilde{h}_{it}^b]h~it=[h~itf,h~itb],得到隐藏状态hith_{it}hit的片段级特征表征。
3.4.4 输出层与损失函数
HSSLSTM网络生成输出向量序列Oi=(oi1,oi2,...,oiLi)O_i=(o_{i1}, o_{i2}, ..., o_{iL_i})Oi=(oi1,oi2,...,oiLi),其中第t个输出向量oito_{it}oit(1≤t≤Li1 \leq t \leq L_i1≤t≤Li)由片段级特征表征h~it\tilde{h}_{it}h~it计算得到。
将每个输出向量oito_{it}oit输入softmax层,生成预测标签序列Y^i=(y^i1,y^i2,...,y^iLi)\hat{Y}_i=(\hat{y}_{i1}, \hat{y}_{i2}, ..., \hat{y}_{iL_i})Y^i=(y^i1,y^i2,...,y^iLi),其中y^it\hat{y}_{it}y^it为第i个样本第t个脉冲属于所有类别的概率分布。通过该概率分布,可分类脉冲序列P中存在的所有工作模式类别,并确定各类别的过渡边界。
所提HSSLSTM网络对所有输入序列中脉冲的分类错误进行惩罚,N个训练序列样本的序列损失函数Eˉ\bar{E}Eˉ定义为:
Eˉ=1N∑i=1N(−1Li∑t=1Liyitlog(y^it))+λ2∥ω∥22\bar{E} = \frac{1}{N} \sum_{i=1}^{N} \left( -\frac{1}{L_i} \sum_{t=1}^{L_i} y_{it} \log(\hat{y}_{it}) \right) + \frac{\lambda}{2} \|\omega\|_2^2Eˉ=N1i=1∑N(−Li1t=1∑Liyitlog(y^it))+2λ∥ω∥22
其中,Ei=−1Li∑t=1Liyitlog(y^it)E_i = -\frac{1}{L_i} \sum_{t=1}^{L_i} y_{it} \log(\hat{y}_{it})Ei=−Li1∑t=1Liyitlog(y^it)表示第i个序列样本的序列损失;LiL_iLi(i=1,2,...,Ni=1,2,...,Ni=1,2,...,N)为第i个脉冲序列样本的脉冲数;yity_{it}yit为第i个样本第t个脉冲的真实标签;y^it\hat{y}_{it}y^it为对应的分类输出;正则项λ2∥ω∥22\frac{\lambda}{2} \|\omega\|_2^22λ∥ω∥22用于降低过拟合风险,其中ω\omegaω为权重向量,λ\lambdaλ为正则化系数。HSSLSTM网络的训练目标是最小化N个训练样本的序列损失。
4 实验验证
为验证所提框架的有效性与优越性,本文基于仿真MFR工作模式脉冲序列开展实验。4.1节介绍实验设计(含仿真设置、评价指标与基准方法);4.2节与4.3节分别呈现实验结果与分析。
4.1 实验设计
4.1.1 仿真设置
参考表1,基于PRI、RF、PW三参数脉冲间调制模式的不同组合,人工定义5类工作模式(即K=5K=5K=5)。脉冲及调制参数的取值范围参考文献[23],如表2所示。对于每个脉冲序列样本,不同类别的脉冲与调制参数从表2的区间内随机生成(服从均匀分布)。从统计角度看,不同类别的初始参数区间存在重叠,因此要求所提方法主要依赖序列特征完成分类任务。
表2 脉冲及调制参数的取值范围(U(⋅)U(\cdot)U(⋅)表示均匀分布)
| 调制参数 | PRI | RF | PW |
|---|---|---|---|
| 脉冲参数初始区间 | U(100,200)U(100,200)U(100,200) μs | U(9×103,9.2×103)U(9 \times 10^3, 9.2 \times 10^3)U(9×103,9.2×103) MHz | U(1,50)U(1,50)U(1,50) μs |
| 捷变脉冲组数 | U(2,16)U(2,16)U(2,16) | U(2,16)U(2,16)U(2,16) | U(2,8)U(2,8)U(2,8) |
| 驻留切换脉冲组数 | U(2,8)U(2,8)U(2,8) | U(2,8)U(2,8)U(2,8) | - |
| 每组脉冲数 | U(8,12)U(8,12)U(8,12) | U(8,12)U(8,12)U(8,12) | - |
| 抖动偏差(均值占比) | U(5%,30%)U(5\%,30\%)U(5%,30%) | U(5%,30%)U(5\%,30\%)U(5%,30%) | - |
| 滑动偏差(均值占比) | U(2,8)U(2,8)U(2,8) | - | - |
表3 7种混合场景参数
| 场景编号 | 测量噪声(μs, MHz, μs) | 丢失脉冲占比(%) | 杂波脉冲占比(%) |
|---|---|---|---|
| 1 | (0, 0, 0) | 0 | 0 |
| 2 | (0.5, 0.5, 0.05) | 5 | 10 |
| 3 | (1, 1, 0.1) | 10 | 20 |
| 4 | (1.5, 1.5, 0.15) | 15 | 30 |
| 5 | (2, 2, 0.2) | 20 | 40 |
| 6 | (2.5, 2.5, 0.25) | 25 | 50 |
| 7 | (3, 3, 0.3) | 30 | 60 |
本文制备两类数据集:
- 第一类数据集:包含“片段标注数据集(SLD)”与“脉冲标注序列数据集(PLSD)”。SLD中每个序列样本仅包含一个工作模式片段及对应类别标签,用于训练seq2one模型;PLSD基于3.2节的序列制备步骤,由SLD生成,用于训练所提seq2seq方法。
- 第二类数据集:用于脉冲级测试,包含“类别数量可变数据集(VNCD)”与“片段数量可变数据集(VNSD)”。其中:
- VNCD=⋃k=15VNCDkVNCD = \bigcup_{k=1}^5 VNCD_kVNCD=⋃k=15VNCDk,kkk(1≤k≤5)为VNCDkVNCD_kVNCDk中的工作模式类别数,且VNCDkVNCD_kVNCDk的片段数J=kJ=kJ=k(每个片段分属唯一类别);
- VNSD=⋃JVNSDJVNSD = \bigcup_{J} VNSD_JVNSD=⋃JVNSDJ,JJJ(1,2,3,4,5,10,15,20,…,100)为VNSDJVNSD_JVNSDJ中的片段数,这些片段通过“频繁过渡(FT)”与“非频繁过渡(INFT)”两种类别过渡策略生成。FT策略中,序列中不同工作模式类别随机过渡;INFT策略基于文献[19]的过渡矩阵(模拟实际MFR的模式过渡关系),雷达更可能保持当前工作模式而非切换到其他模式,因此序列中类别过渡频率较低。
两类数据集均考虑三种非理想因素:测量噪声、丢失脉冲与杂波脉冲[23,27,28,46],并设置三种基础非理想场景:
- 仅测量噪声(MNO):为PRI、RF、PW的观测值添加高斯分布测量噪声(均值为0,标准差σ=[σPRI(μs),σRF(MHz),σPW(μs)]\sigma=[\sigma_{\text{PRI}}(\mu\text{s}), \sigma_{\text{RF}}(\text{MHz}), \sigma_{\text{PW}}(\mu\text{s})]σ=[σPRI(μs),σRF(MHz),σPW(μs)])。设计7个噪声等级,σPRI\sigma_{\text{PRI}}σPRI从0到3 μs(步长0.5),σRF\sigma_{\text{RF}}σRF从0到3 MHz(步长0.5),σPW\sigma_{\text{PW}}σPW从0到0.3 μs(步长0.05)。例如,第1等级σ1=[0 μs,0 MHz,0 μs]\sigma_1=[0\ \mu\text{s}, 0\ \text{MHz}, 0\ \mu\text{s}]σ1=[0 μs,0 MHz,0 μs],第2等级σ2=[0.5 μs,0.5 MHz,0.05 μs]\sigma_2=[0.5\ \mu\text{s}, 0.5\ \text{MHz}, 0.05\ \mu\text{s}]σ2=[0.5 μs,0.5 MHz,0.05 μs]。
- 仅丢失脉冲(LPO):仅考虑包含一定比例丢失脉冲的序列,测量噪声固定为σ=[1.5 μs,1.5 MHz,0.15 μs]\sigma=[1.5\ \mu\text{s}, 1.5\ \text{MHz}, 0.15\ \mu\text{s}]σ=[1.5 μs,1.5 MHz,0.15 μs],丢失脉冲占比设为17个等级(0%~80%,步长5%)。
- 仅杂波脉冲(SPO):仅考虑包含一定比例杂波脉冲的序列,测量噪声同样固定为σ=[1.5 μs,1.5 MHz,0.15 μs]\sigma=[1.5\ \mu\text{s}, 1.5\ \text{MHz}, 0.15\ \mu\text{s}]σ=[1.5 μs,1.5 MHz,0.15 μs],杂波脉冲占比设为17个等级(0%~80%,步长5%)。
此外,定义7种混合场景(如表3所示),以评估非理想因素联合作用对方法性能的影响。
HSSLSTM网络采用Adam优化器[47],学习率为10−310^{-3}10−3,批大小为64;经多次实验验证,两层隐藏状态向量的维度均设为128;为降低过拟合,在片段级bi-LSTM层后添加dropout层( dropout系数为0.25)[48];正则化系数λ=10−4\lambda=10^{-4}λ=10−4,最大训练轮次为300。所提HSSLSTM与基准深度学习模型(见4.1.3节)均基于MATLAB R2018b深度学习工具箱实现。
4.1.2 评价指标
传统seq2one方法的准确率(accseq2oneacc_{\text{seq2one}}accseq2one)定义为正确分类的序列样本数占总样本数的比例。脉冲级识别任务需关注每个脉冲的分类准确率,因此需调整准确率计算方式以适应脉冲级识别方法(accpulseacc_{\text{pulse}}accpulse)。
为便于对比分析,本文中seq2one方法与脉冲级识别方法的准确率计算公式如下:
seq2one方法:
I[y^i=yi]={1,若 y^i=yi0,否则\mathbb{I}[\hat{y}_i = y_i] = \begin{cases}
1, & \text{若}\ \hat{y}_i = y_i \\
0, & \text{否则}
\end{cases}I[y^i=yi]={1,0,若 y^i=yi否则
accseq2one=1N∑i=1NI[y^i=yi]acc_{\text{seq2one}} = \frac{1}{N} \sum_{i=1}^{N} \mathbb{I}[\hat{y}_i = y_i]accseq2one=N1i=1∑NI[y^i=yi]
脉冲级识别方法:
accpulse=1N∑i=1N1Li∑t=1LiI[y^it=yit]acc_{\text{pulse}} = \frac{1}{N} \sum_{i=1}^{N} \frac{1}{L_i} \sum_{t=1}^{L_i} \mathbb{I}[\hat{y}_{it} = y_{it}]accpulse=N1i=1∑NLi1t=1∑LiI[y^it=yit]
式中,NNN为测试样本数;y^i\hat{y}_iy^i(seq2one方法)为第i个样本的预测标签,y^it\hat{y}_{it}y^it(脉冲级方法)为第i个样本第t个脉冲的预测标签;yiy_iyi(seq2one方法)为第i个样本的真实标签,yity_{it}yit(脉冲级方法)为第i个样本第t个脉冲的真实标签;LiL_iLi为第i个测试样本的脉冲数;I[⋅]\mathbb{I}[\cdot]I[⋅]为指示函数。
4.1.3 基准方法与实验规划
为定量评估所提脉冲级识别框架的有效性与效率,选取以下具有竞争力的脉冲级基准方法:
(1)seq2one方案的基础分类方法
首先分析三种基于seq2one方案的基础分类方法性能:
- FANN:基于手工特征的人工神经网络方法。参考文献[23]的直方图特征与序列特征,并扩展至三参数场景,分类器采用反向传播神经网络。
- CNN:参考文献[27]用于PRI调制识别的CNN,并扩展至三参数场景。
- SOLSTM:参考文献[28]用于seq2one分类的单层bi-LSTM分类器。
采用包含四种非理想场景的SLD数据集评估上述三种seq2one分类器的性能,且其他场景与脉冲级识别实验的实现设置保持一致。以仅测量噪声场景为例:SLD数据集中每个噪声等级生成1000个样本,共7000个样本;按7:1.5:1.5的比例划分为训练集、验证集与测试集;使用训练集与验证集训练三种seq2one分类器,在测试集的每个噪声等级上分别测试,得到7组测试结果,如图5所示。
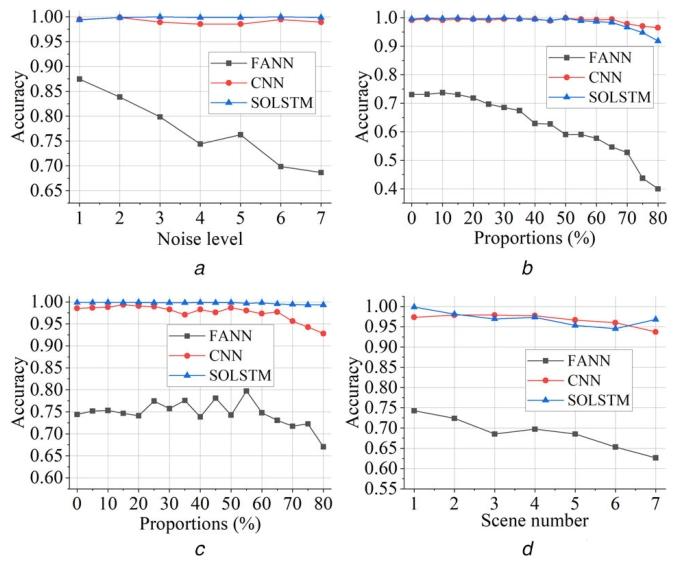
图5 四种非理想场景下的seq2one分类结果
(a)仅测量噪声;(b)仅丢失脉冲;(c)仅杂波脉冲;(d)混合场景。
总体而言,CNN与SOLSTM在seq2one分类中表现良好,四种场景下的准确率均接近1.0(超过0.9)。这得益于深度学习网络(如CNN、SOLSTM)从高非理想数据中提取有效模式内特征的强大能力,同时也归因于联合使用PRI、RF、PW三参数向量(其中RF与PW参数受丢失脉冲与杂波脉冲的影响较小)。然而,FANN在四种非理想场景下均表现最差,表明手工特征提取方法在面对非理想数据时失效。
(2)脉冲级基准方法
将上述三种seq2one分类器与滑动窗口技术[23]结合,构建三种脉冲级基准方法,以“SL-”为前缀命名为SL-FANN、SL-CNN与SL-SOLSTM。参考文献[23],选取拒绝阈值并丢弃低于该阈值的窗口处理结果;同时,对连续窗口中重叠脉冲的分类结果进行集成(投票)。由于片段样本的脉冲数服从U(200,300)U(200,300)U(200,300)的均匀分布,窗口长度设为250;经多次实验验证,滑动步长设为25,以平衡滑动窗口的计算开销。
此外,通过移除所提HSSLSTM的片段级bi-LSTM层,构建第四种基准方法——单层LSTM(SSLSTM),用于对比HSSLSTM分层特征学习的优势。
(3)实验规划
基于上述数据集与基准方法,设计脉冲级识别的完整实验流程(如图6所示),实验结果与分析聚焦以下两个方面:
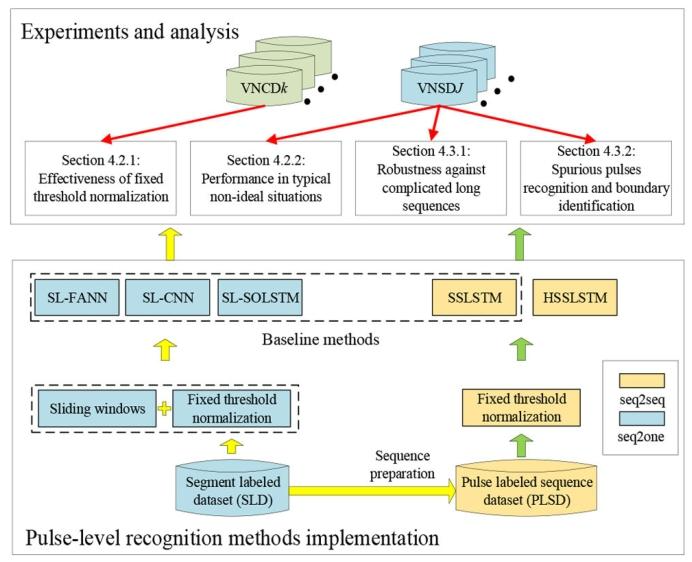
图6 脉冲级识别方法实现与实验设计
A:所提框架的实现验证
(1)固定阈值归一化的有效性(4.2.1节);
(2)方法在典型非理想场景下的性能(4.2.2节)。
B:HSSLSTM模型的扩展能力
(1)方法对复杂长序列的鲁棒性(4.3.1节);
(2)杂波脉冲识别与边界检测能力(4.3.2节)。
4.2 所提框架的实现验证
4.2.1 固定阈值归一化的有效性
本实验使用PLSD与SLD数据集分别训练HSSLSTM与基准模型,使用VNCD数据集测试。在VNCDkVNCD_kVNCDk中,每个样本包含kkk(1≤k≤5)个工作模式类别,且片段数J=kJ=kJ=k。4.2节与4.3节均采用脉冲级准确率作为评价指标。
根据3.3节的固定阈值归一化方法,设置PRI、RF、PW的归一化下界分别为100 μs、9000 MHz、1 μs,上界分别为200 μs、9200 MHz、50 μs。训练阶段仅考虑“仅测量噪声”场景,测试样本的噪声参数设为σ=[1.5 μs,1.5 MHz,0.15 μs]\sigma=[1.5\ \mu\text{s}, 1.5\ \text{MHz}, 0.15\ \mu\text{s}]σ=[1.5 μs,1.5 MHz,0.15 μs]。
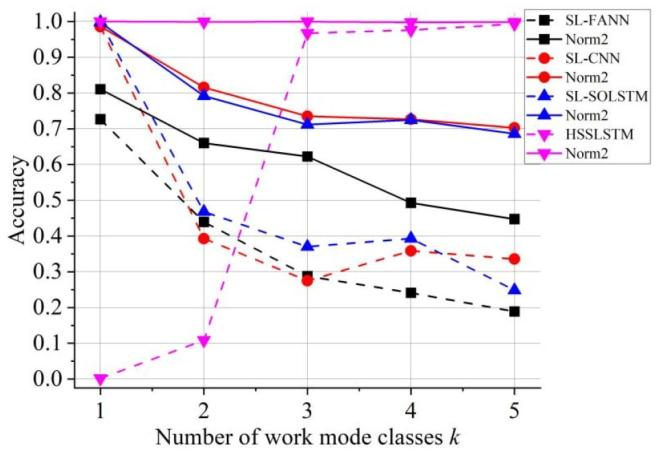
实验结果如图7所示:在类别数量变化的情况下,采用固定阈值归一化的HSSLSTM性能均优于SL-FANN、SL-CNN与SL-SOLSTM;此外,相较于传统归一化方法,固定阈值归一化方法对四种方法的性能均有提升。这表明,当序列中缺失部分模式类别时,传统归一化方法会破坏类别间的相对关系,导致seq2seq与seq2one方法的性能均下降。
图7 不同归一化方法下的脉冲级识别性能
虚线与实线分别表示传统归一化方法与所提固定阈值归一化方法(记为“norm2”)。
当测试样本中仅包含12个工作模式类别时,采用传统归一化方法的HSSLSTM性能远未达到理想水平。由于HSSLSTM同时学习模式内与模式间特征,当仅存在12个类别时,传统归一化导致的关系破坏带来的性能损失,超过了模式间特征带来的性能提升;随着序列中类别数量增加,模式间特征带来的性能提升迅速增大,最终超过关系破坏带来的损失。例如,当k≥3k \geq 3k≥3时,采用传统归一化方法的HSSLSTM性能甚至优于采用固定阈值归一化的SL-CNN与SL-SOLSTM。
由于固定阈值归一化不会破坏模式内与模式间关系,后续章节的训练与测试均采用该方法。
4.2.2 典型非理想场景下的性能
脉冲流在电磁环境中易受污染,导致脉冲序列呈现高度非理想特性,因此优秀的识别方法需具备鲁棒性,能对污染脉冲序列进行正确识别。本实验评估不同方法在非理想场景(包括测量噪声、丢失脉冲、杂波脉冲三种单独场景与7种混合场景)下的性能:训练数据集为SLD与PLSD(见4.1.3节示例),测试数据集为J=15J=15J=15的VNSD_J,且VNSD_J采用INFT策略模拟模式过渡。
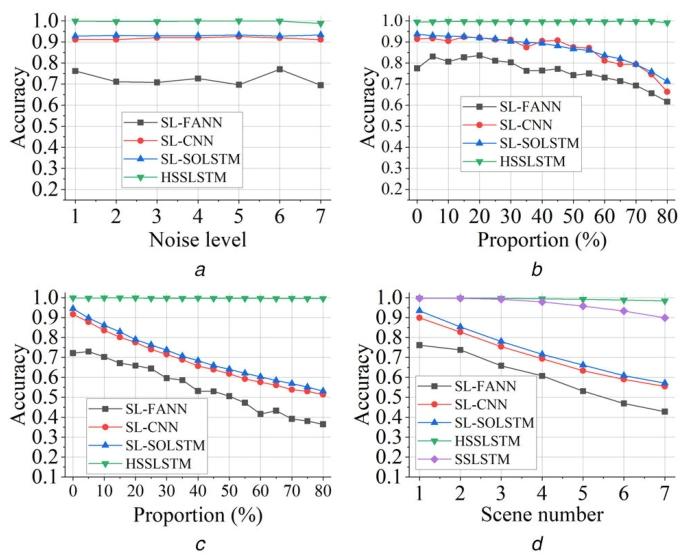
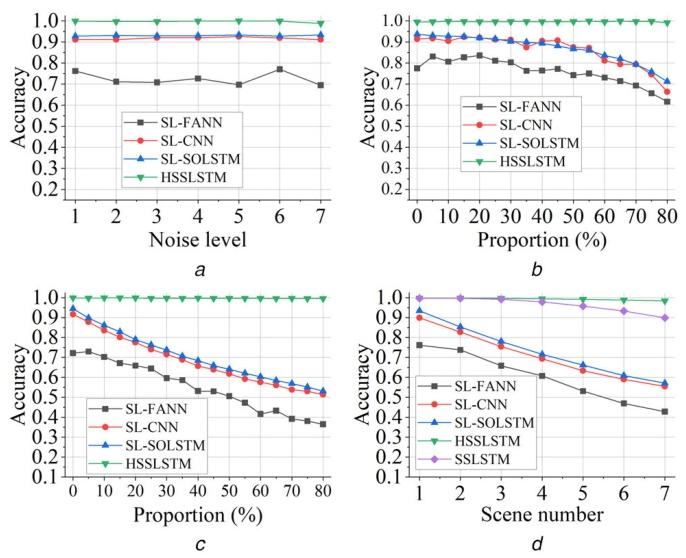
实验结果如图8所示:在所有测试场景中,HSSLSTM性能均优于其他三种基准方法。具体分析各场景:
- 仅测量噪声场景:所有方法均表现稳定,SL-CNN与SL-SOLSTM的准确率甚至超过0.9;
- 丢失脉冲/杂波脉冲场景:三种滑动窗口方法的性能随场景恶化(丢失/杂波占比增加)逐渐下降,其中SL-FANN性能最差;
- 混合场景:尽管在seq2one分类中(图5)CNN与SOLSTM准确率接近100%且对非理想场景鲁棒,但在脉冲级识别中(图8)性能显著下降。
图8 不同非理想场景下各脉冲级识别方法的性能
(a)仅测量噪声;(b)仅丢失脉冲;(c)仅杂波脉冲;(d)混合场景。
对于杂波脉冲场景:在仅杂波脉冲与混合场景中,三种基于seq2one的方法性能随杂波脉冲占比增加近似线性下降。由于seq2one方法每次对整个处理窗口进行分类,无法对杂波脉冲进行单独分类;而所提HSSLSTM在训练阶段将杂波脉冲标注为第K+1类,因此在测试阶段可对脉冲序列中的每个杂波脉冲进行正确分类。由于杂波脉冲不包含序列特征,HSSLSTM可轻松识别。
在混合场景实验中,新增SSLSTM作为第四种基准方法。结果显示,在复杂场景(如场景4~7)下,HSSLSTM的学习效率与性能均优于SSLSTM,这是因为HSSLSTM的分层结构与工作模式序列的分层特性一致。
综上,尽管基准方法可实现脉冲级识别,但在实际非理想场景下,其性能远不如所提HSSLSTM。
4.3 基于seq2seq结构的扩展能力
本节从两个方面验证所提HSSLSTM基于seq2seq结构的扩展能力:(1)对复杂长序列的识别能力;(2)杂波脉冲标注与过渡边界检测能力。
4.3.1 对复杂长序列的识别能力
实际应用中,截获的脉冲序列以无限脉冲流形式存在,分类器需识别长输入序列中包含的多类别,面临三大挑战:类别数量未知、片段重复出现、类别持续时长可变、输入序列首尾片段可能被截断。本实验评估所提框架对包含可变数量片段与截断片段的长序列的识别性能:使用SLD数据集训练三种基于seq2one的基准方法,使用PLSD数据集训练所提HSSLSTM;基于片段数JJJ,在VNSD_J数据集上评估四种方法的性能;采用FT与INFT两种过渡策略,为每个JJJ从5个工作模式类别中生成200个序列样本;训练阶段仅考虑“仅测量噪声”场景,测试阶段在VNSD_J中添加σ=[1.5 μs,1.5 MHz,0.15 μs]\sigma=[1.5\ \mu\text{s}, 1.5\ \text{MHz}, 0.15\ \mu\text{s}]σ=[1.5 μs,1.5 MHz,0.15 μs]的测量噪声。
图9展示了片段数JJJ变化时的识别准确率:采用固定阈值归一化的HSSLSTM(实线)在FT与INFT策略下,对所有JJJ的识别准确率均接近100%,避免了传统归一化方法的缺陷。
图9 片段数可变样本的识别准确率
(a)FT策略;(b)INFT策略。
对于三种基准模型:
- 在INFT策略下,SL-FANN、SL-CNN与SL-SOLSTM的整体性能优于FT策略。由于INFT策略中雷达更可能保持当前模式而非切换,序列稳定性更高,因此滑动窗口处理在稳定序列上的性能更优;
- 当测试样本仅包含1个片段时,SL-CNN与SL-SOLSTM的准确率接近100%;随着片段数增加,性能先急剧下降(J=2J=2J=2时),随后在FT策略下缓慢下降,在INFT策略下缓慢上升。当J=2J=2J=2时,两个片段可能分属不同类别,序列复杂度增加,导致性能显著下降;随着JJJ继续增加,FT策略下类别过渡更频繁,性能因片段数增加进一步缓慢下降;而INFT策略下类别过渡频率低,过渡带来的性能提升超过片段数增加带来的损失,因此性能缓慢上升。
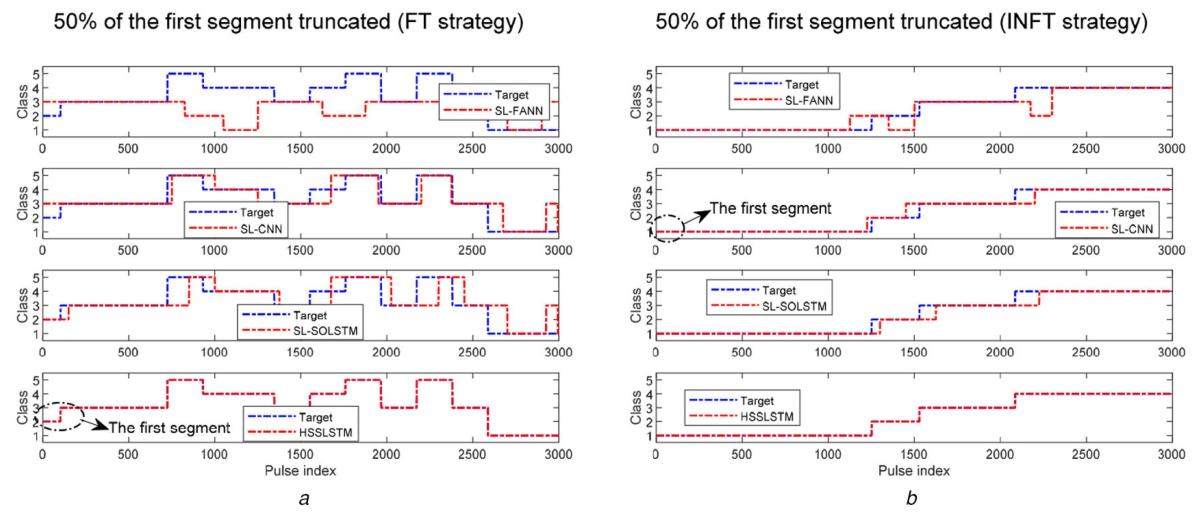
图10展示了“首段50%脉冲被截断”的脉冲序列的识别结果:得益于seq2seq方案的优势,所提HSSLSTM几乎不受截断影响;而滑动窗口方法在截断片段后发生模式过渡时,会产生分类误差。例如,图10a中,SL-FANN与SL-CNN将首段脉冲(真实标签“2”)分类为与第二段脉冲(真实标签“3”)相同的标签,SL-SOLSTM则将第二段部分脉冲分类为与首段相同的标签;而当截断后未发生模式过渡时(图10b),截断的影响大幅缓解,所有方法均可正确识别截断片段与后续片段的脉冲标签。
图10 首段50%脉冲被截断的脉冲序列的识别结果
(a)FT策略;(b)INFT策略。
综上,与SL-FANN、SL-CNN、SL-SOLSTM相比,所提HSSLSTM可精准识别复杂长序列中每个脉冲的类别标签。
4.3.2 杂波脉冲识别与边界检测能力
HSSLSTM的另一重要优势是其脉冲级输出结果:可区分目标脉冲中的杂波脉冲,并精准检测序列中相邻类别的过渡边界。
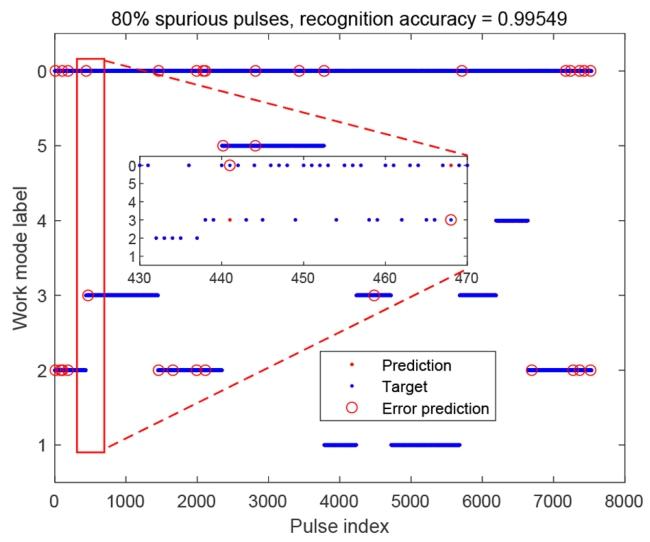
图11展示了HSSLSTM对“含80%杂波脉冲的序列”的脉冲级识别结果。为增加识别复杂度,杂波脉冲参数的统计区间与真实脉冲一致,迫使方法需通过挖掘序列特征识别杂波脉冲。图11显示,所有杂波脉冲均被预测为“0类”,识别准确率达99.55%;相比之下,传统seq2one方法无法对杂波脉冲进行分类。
图11 含80%杂波脉冲的序列识别结果
蓝色与红色圆点分别表示每个脉冲的真实标签与预测标签;红色圆圈标记的“错误预测”表示标签预测错误的脉冲。需注意,除错误预测脉冲外,大部分红色圆点被蓝色圆点覆盖(即预测正确)。横轴表示脉冲索引,纵轴表示工作模式类别标签(“0类”为杂波脉冲,“1~5类”为5种工作模式)。
一旦获取每个脉冲的类别标签,即可通过HSSLSTM实现类别过渡边界的检测:设包含L个脉冲的归一化脉冲序列样本为Pi=(pi1,pi2,...,piL)P_i=(p_{i1}, p_{i2}, ..., p_{iL})Pi=(pi1,pi2,...,piL),HSSLSTM输出预测标签序列Y^i=(y^i1,y^i2,...,y^iL)\hat{Y}_i=(\hat{y}_{i1}, \hat{y}_{i2}, ..., \hat{y}_{iL})Y^i=(y^i1,y^i2,...,y^iL);移除所有预测为杂波脉冲的标签后,若连续两个脉冲的标签满足y^it≠y^i(t+1)\hat{y}_{it} \neq \hat{y}_{i(t+1)}y^it=y^i(t+1),则表明发生模式过渡。
所提HSSLSTM的脉冲级识别能力在脉冲解交织中具有重要应用潜力:在混合脉冲序列中,可将其他辐射源的脉冲视为“杂波脉冲”,与目标辐射源的脉冲区分开。
5 结论
识别截获MFR脉冲序列中的多类工作模式并检测各类别的精准边界,是战术对抗与干扰对抗的关键预处理步骤。
本文将MFR工作模式识别与边界检测建模为脉冲级识别问题,指出seq2seq方法是实现该任务的直观且可行的方案,并提出一种基于HSSLSTM的新型脉冲级工作模式识别框架,该框架包含三个连续步骤:(1)序列制备;(2)固定阈值归一化;(3)HSSLSTM构建。实验结果表明,所提框架可实现脉冲级精准识别,能处理包含任意数量已知类别、任意数量片段且类别脉冲数动态变化的脉冲序列。此外,该新型序列表征与识别框架可推广至多种脉冲序列识别与边界检测任务。
然而,所提方法仍存在局限性,需进一步研究以完善雷达工作模式序列分析:
- 若需将杂波脉冲识别为第K+1类(而非污染的训练类别),所提seq2seq方法需在训练数据集中对杂波脉冲进行大量标注,而对实际数据进行此类细粒度标注耗时费力;
- 随着候选类别数量增加,训练序列会变得冗长复杂,需更强大的深度学习模型与专用损失函数以保证性能;
- 所提方法属于监督学习,需提前使用已知类别的脉冲序列样本进行训练。但随着自适应MFR、认知MFR等新型MFR的发展,其控制参数可实时调整,会为训练良好的监督分类器带来新类别。因此,一方面需改进所提方法,使其能检测接收脉冲流中的未训练新类别;另一方面需研究基于无监督序列聚类与控制参数估计的方法,以分析新型MFR的工作模式。
6 致谢
本研究得到中国国家自然科学基金(项目编号:61901032、61976019)资助。作者感谢编辑与匿名评审专家提出的宝贵意见,助力提升本文质量。
7 参考文献
[1] Wiley, R.G.Ebrary, inc.: ‘ELINT: the interception and analysis of radar signals’ (Artech House, Boston, 2006)
[2] Weber, M.E., Cho, J.Y.N., Thomas, H.G.: ‘Command and control for multifunction phased array radar’, IEEE Trans. Geosci. Remote Sens., 2017, 55, (10), pp. 5899–5912
[3] Stailey, J.E., Hondl, K.D.: ‘Multifunction phased array radar for aircraft and weather surveillance’, Proc. IEEE, 2016, 104, (3), pp. 649–659
[4] Mir, H.S., Guitouni, A.: ‘Variable dwell time task scheduling for multifunction radar’, IEEE Trans. Autom. Sci. Eng., 2014, 11, (2), pp. 463–472
[5] Boers, Y., Driessen, H, Zwaga, J.: ‘Adaptive MFR parameter control: fixed against variable probabilities of detection’, IEE Proc. - Radar Sonar Navig., 2006, 153, (1), pp. 2–6
[6] Arasaratnam, I., Haykin, S., Kirubarajan, T., et al.: ‘Tracking the mode of operation of multi-function radars’. IEEE Conf. on Radar. Verona, NY, USA, 2006
[7] Visnevski, N., Krishnamurthy, V., Wang, A., et al.: ‘Syntactic modeling and signal processing of multifunction radars: a stochastic context-free grammar approach’, Proc. IEEE, 2007, 95, (5), pp. 1000–1025
[8] Roe, J., Pudner, A.: ‘The real-time implementation of emitter identification for ESM’. IEE Colloquium on Signal Processing in Electronic Warfare, London, UK, 1994, pp. 7/1–7/6
[9] Wilkinson, D.R., Watson, A.W.: ‘Use of metric techniques in ESM data processing’, IEE Proc. F - Commun. Radar Signal Process., 1985, 132, (4), pp. 229–232
[10] Ata, A.W., Abdullah, S.N.: ‘Deinterleaving of radar signals and PRF identification algorithms’, IET Radar Sonar Navig., 2007, 1, (5), pp. 340–347
[11] Visnevski, N.A.: ‘Syntactic modeling of multi-function radars’. PhD thesis, McMaster University, 2005
[12] Wang, A., Krishnamurthy, V.: ‘Threat estimation of multifunction radars: modeling and statistical signal processing of stochastic context free grammars’. IEEE Int. Conf. on Acoustics, Honolulu, HI, 2007, pp. II-793–III-796
[13] Wang, A., Krishnamurthy, V.: ‘Signal interpretation of multifunction radars: modeling and statistical signal processing with stochastic context free grammar’, IEEE Trans. Signal Process., 2008, 56, (3), pp. 1106–1119
[14] Visnevski, N., Krishnamurthy, V., Haykin, S., et al.: ‘Multi-function radar emitter modelling: a stochastic discrete event system approach’. IEEE Conf. on Decision & Control, Maui, HI, 2003, Vol. 6, pp. 6295–6300
[15] Visnevski, N., Haykin, S., Krishnamurthy, V., et al.: ‘Hidden Markov models for radar pulse train analysis in electronic warfare’. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Philadelphia, PA, 2005, Vol. 5, pp. v/597–v/600
[16] Li, C., Wang, W., Wang, X.: ‘A method for extracting radar words of multi-function radar at data level’. Int. Radar Conf., Xi’an, China, 2013, pp. 1–5
[17] Dai, L.P., Wang, B., Jia, L., et al.: ‘A method for states estimation of multifunction radar based on stochastic context free grammar’, J. Air Force Eng. Univ., 2014, 15, (3), pp. 24–28
[18] Ou, J., Chen, Y., Zhao, F., et al.: ‘A method for operating mode identification of multi-function radars based on predictive state representations’, IET Radar Sonar Navig., 2017, 11, (3), pp. 426–433
[19] Ou, J., Chen, Y., Zhao, F., et al.: ‘Novel approach for the recognition and prediction of multi-function radar behaviours based on predictive state representations’, Sensors, 2017, 17, (3), p. 632
[20] Ou, J., Chen, Y., Zhao, F., et al.: ‘Novel method for radar word extraction in the syntactic model of multi-function radar’. 18th Int. Radar Symp., Prague, 2017, pp. 1–7
[21] Liu, H., Yu, H., Sun, Z., et al.: ‘Multi-function radar emitter identification based on stochastic syntax-directed translation schema’, Chin. J. Aeronaut., 2014, 27, (6), pp. 166–173
[22] Ou, J., Chen, Y., Zhao, F., et al.: ‘Research on extension of hierarchical structure for multi-function radar signals’. 2017 Progress in Electromagnetics Research Symp., St. Petersburg, 2017, pp. 2612–2616
[23] Kauppi, J.P., Martikainen, K., Ruotsalainen, U.: ‘Hierarchical classification of dynamically varying radar pulse repetition interval modulation patterns’, Neural Netw., 2010, 23, (10), pp. 1226–1237
[24] Liu, Y., Zhang, Q.: ‘An improved algorithm for PRI modulation recognition’. 2017 IEEE Int. Conf. on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 2017, pp. 1–5
[25] Hu, G., Liu, Y.: ‘An efficient method of pulse repetition interval modulation recognition’. Int. Conf. on Communications & Mobile Computing, Shenzhen, China, 2010, pp. 287–291
[26] Mahmoud, K.P., Mansour, A., Forouhar, F.: ‘A new method for detection of complex pulse repetition interval modulations’. IEEE 11th Int. Conf. on Signal Processing, Beijing, China, 2012, pp. 1705–1709
[27] Li, X., Huang, Z., Wang, F., et al.: ‘Toward convolutional neural networks on pulse repetition interval modulation recognition’, IEEE Commun. Lett., 2018, 22, (11), pp. 2286–2289
[28] Liu, Z.M., Yu, P.S.: ‘Classification, denoising and deinterleaving of pulse streams with recurrent neural networks’, IEEE Trans. Aerosp. Electron. Syst., 2019, 55, (4), pp. 1624–1639
[29] Bahdanau, D., Cho, K., Bengio, Y.: ‘Neural machine translation by jointly learning to align and translate’ (Computer Science, arXiv, 2014)
[30] Luong, M.-T., Pham, H.: ‘Manning, effective approaches to attention-based neural machine translation’, arXiv, 2015
[31] Ma, X., Hovy, E.: ‘End-to-end sequence labeling via Bi-directional LSTM-CNNs-CRF’, arXiv, 2016
[32] Al-Sabahi, K., Zuping, Z, Nadher, M.: ‘A hierarchical structured self-attentive model for extractive document summarization (HSSAS)’, IEEE Access, 2018, 6, pp. 24205–24212
[33] Gao, L., Li, X., Song, J., et al.: ‘Hierarchical LSTMs with adaptive attention for visual captioning’, IEEE Trans. Pattern Anal. Mach. Intell., 2020, 42, pp. 1112–1131
[34] Phan, H., Andreotti, F., Cooray, N., et al.: ‘Seqsleepnet: end-to-end hierarchical recurrent neural network for sequence-to-sequence automatic sleep staging’, IEEE Trans. Neural Syst. Rehabil. Eng., 2019, 27, (3), pp. 400–410
[35] Kutsuzawa, K., Sakaino, S, Tsuji, T.: ‘Sequence-to-sequence model for trajectory planning of nonprehensile manipulation including contact model’, IEEE Robot. Autom. Lett., 2018, 3, (4), pp. 3606–3613
[36] Deng, Y., Wang, L., Jia, H., et al.: ‘A sequence-to-sequence deep learning architecture based on bidirectional GRU for type recognition and time location of combined power quality disturbance’, IEEE Trans. Ind. Inf., 2019, 15, (8), pp. 4481–4493
[37] Miranda, S., Baker, C., Woodbridge, K., et al.: ‘Knowledge-based resource management for multifunction radar: a look at scheduling and task prioritization’, IEEE Signal Process. Mag., 2006, 23, (1), pp. 66–76
[38] Miranda, S.L.C., Baker, C.J., Woodbridge, K., et al.: ‘Comparison of scheduling algorithms for multifunction radar’, IET Radar Sonar Navig., 2007, 1, (6), pp. 414–424
[39] Winter, É., Baptiste, P.: ‘On scheduling a multifunction radar’, Aerosp. Sci. Technol., 2007, 11, (4), pp. 289–294
[40] Miranda, S.L.C., Baker, C.J., Woodbridge, K., et al.: ‘Fuzzy logic approach for prioritisation of radar tasks and sectors of surveillance in multifunction radar’, IET Radar Sonar Navig., 2007, 1, (2), pp. 131–141
[41] Charlish, A., Katsilieris, F.: ‘Array radar resource management’. Novel Radar Techniques and Applications Volume 1: Real Aperture Array Radar, Imaging Radar, and Passive and Multistatic Radar’ (Institution of Engineering and Technology, 2017), pp. 135–171
[42] Zolhavarieh, S., Aghabozorgi, S, The, Y.W.: ‘A review of subsequence time series clustering’, Scientific World J., 2014, 2014, pp. 1–19
[43] Hochreiter, S., Schmidhuber, J.: ‘Long short-term memory’, Neural Comput., 1997, 9, (8), pp. 1735–1780
[44] Greff, K., Srivastava, R.K., Koutník, J., et al.: ‘LSTM: a search space odyssey’, IEEE Trans. Neural Netw. Learn. Syst., 2017,























 6643
6643

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










