Codeforces Round #716 （A-C）题解

开学之后就没咋打过CF了，天天早八打CF属实有点扛不住，准备蓝桥杯也有一阵没做CF的题了，碰到一场九点半的div2，就试了一把。。。

A. Perfectly Imperfect Array

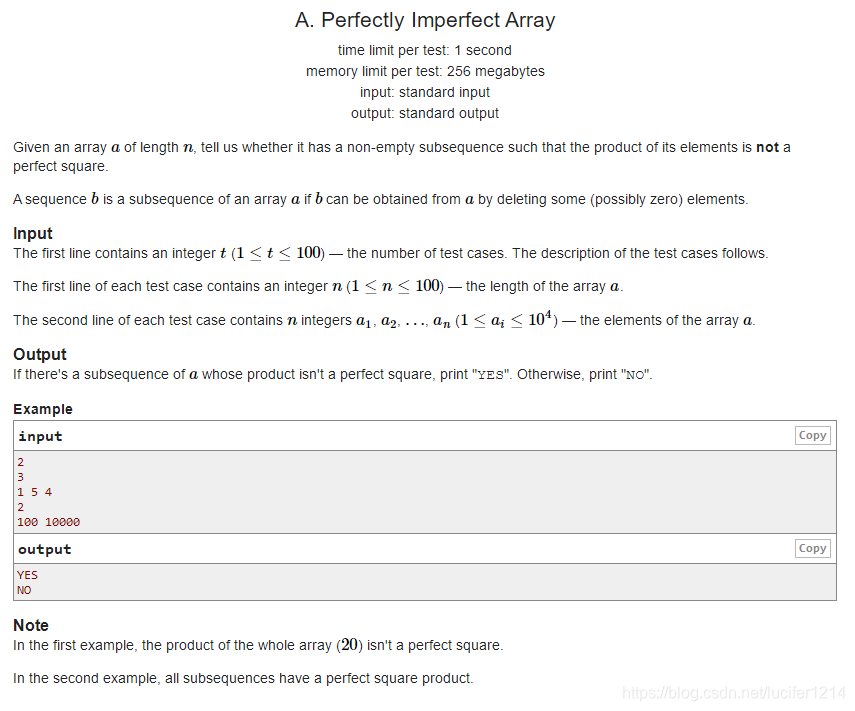
题目大意：给定一个长度为n 的数组a，问是否存在一个非空子序列其中的所有元素的乘积不是一个平方式。
思路：我们只需找到数组中是否存在一个数不是平方数，如果存在这个数，则该数组不成立，若不存在则答案成立。

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>

#include <cstring>

#include<algorithm>

#include <queue>

#include<string>

#include<map>
#define mod 1000000009
using namespace std;
int cnt;
const int N = 100010;
typedef long long ll;
typedef pair<int, int> pii;
int a[N];
map<int, int>mp;
int main() {
	int t;
	cin >> t;
	for (int i = 1; i <= 100; i++) {
		mp[i*i]++;
	}
	while (t--)
	{
		int n;
		cin >> n;
		int flag = 0;
		for (int i = 1; i <= n; i++) {
			cin >> a[i];
			if (mp[a[i]] == 0)flag = 1;
		}
		if (!flag) {
			puts("NO");
		}
		else puts("YES");

	}
}

B. AND 0, Sum Big

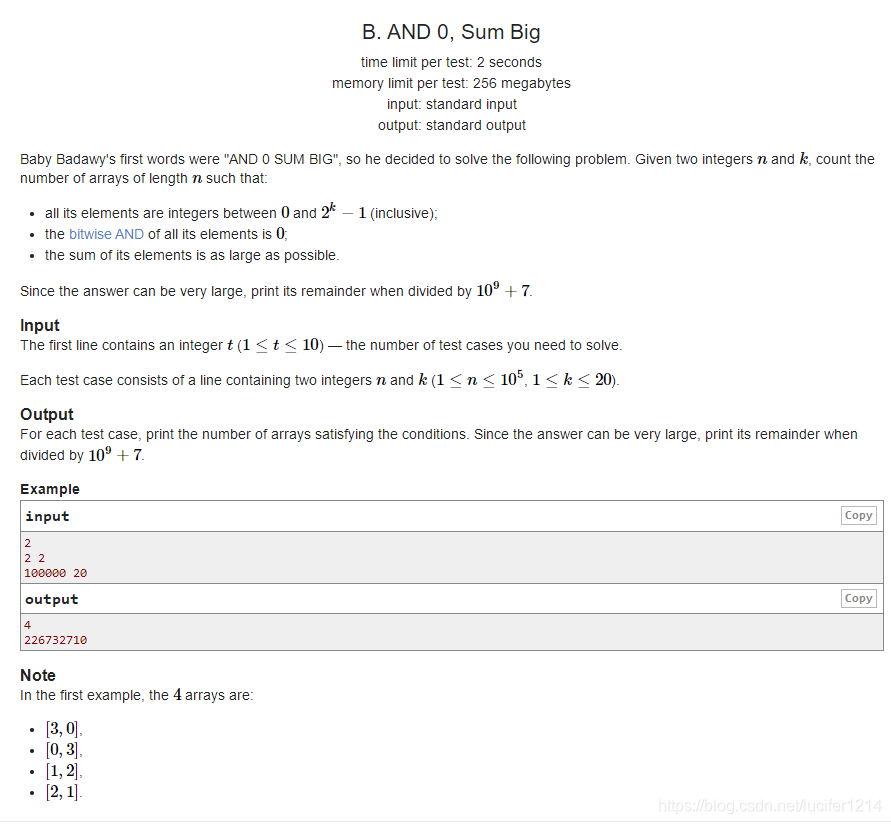
题目大意：
给出n , k 要求输出满足以下条件的数组的数量，答案模1 e 9 + 7 。

（1）数组的元素大小在[ 0 , 2^k-1 ]中
（2）所有元素按位与之后的结果是0。
（3）数组元素的和尽量大。

思路：
赛时看到题人是懵的，赛后仔细思考才明白了题意。其实就是给出n个数，每个数的二进制表达占一行，每个数的二进制表达都是k位，于是我们就组成了一个nk的矩阵，要想使得所有元素按位与之后的结果为0的话，每一列的二进制表达上都必须至少存在一个0，而如果与此同时我们要满足条件3，是元素之和尽量大，所以我们每一列中，只让一个元素为0，即最后变成了一个排列组合问题：在一个nk的矩阵中，另每一列的任一位为0的方案数有多少，答案也就是你n^k.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>

#include <cstring>

#include<algorithm>

#include <queue>

#include<string>

#include<cmath>

#include<map>
#define mod 1000000007
using namespace std;
int cnt;
const int N = 100010;
typedef long long ll;
typedef pair<int, int> pii;
ll a[N];
map<int, int>mp;
int main() {
	int t;
	cin >> t;
	
	while (t--)
	{
		int n, k;
		cin >> n >> k;
		long long ans = 1;
		for (int i = 1; i <= k; i++) {
			ans *= n;
			ans = ans % mod;
		}
		cout << ans << endl;

	}
}

C. Product 1 Modulo N

题目大意：
给出一个数n，从1-n-1挑出几个数组成一个最长序列，该序列的所有元素的乘积mod n = 1。
（赛时理解题意想了半天。。）
思路：
由于要求序列最长，所以所有的答案中都要将1包含进去，随后我们就要寻找我们的答案，首先我们要排除所有与 n 不互质的数，因为如果一个数与 n 不互质那么他的gcd(n, n % x) != 1即此时，任何情况下都不能满足乘积mod n = 1，所以我们将互质的数放入依次数组中，并且计算其乘积 mod n = 1，如果最后发现余数不为 1 ，弹出最后一个数即可（这里听说是威尔逊定理的一个推广，本人对数论研究不深，就不做赘述了）。

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>

#include <cstring>

#include<algorithm>

#include <queue>

#include<string>

#include<cmath>

#include<map>
#define mod 1000000007

using namespace std;
const int N = 100010;
typedef long long ll;
typedef pair<int, int> pii;
ll a[N];
map<int, int>mp;
int n;
int ans[N];
bool st[N];
int gcd(int a, int b) {
	return b ? gcd(b, a % b) : a;
}
int main() {
	ll flag = 1;
	cin >> n;
	int k = 0;
	for (int i = 1; i < n; i++) {
		if (gcd(i, n) == 1) {
			ans[k++] = i;
			flag *= i;
			flag %= n;
		}
	}
	if (flag == 1) {
		cout << k << endl;
		for (int i = 0; i < k; i++)
			cout << ans[i] << ' ';
	}
	else {
		cout << k - 1 << endl;
		for (int i = 0; i < k - 1; i++)
		{
			cout << ans[i] << ' ';
		}
	}
	cout << endl;
}