特征工程

特征工程

特征是从数据中选出能够对模型结果有用的信息。一般可采用专业知识进行选择，但是当数据特征很多时，或者难以通过人工进行选择时，采用数据方法进行筛选。

数据预处理

1.数据缺失

（１）连续值：采用中位数或者均值或者前后值进行填充。
（２）离散值：选择出现频次最多的值进行填充。
当缺失严重值，直接去掉该特征

2.离散值连续化(数值化)

离散特征往往不是数值型，无法直接输入模型，需要数值化。

(1)直接数值化

当离散取值有一定的大小关系时，直接用1,2,3,4…替代。

(2)独特编码(one-hot encoding)

当离散取值没有大小关系时，直接用1,2,3,4会误导模型，采用独热编码可以独立毫无相关的表示特征取值。如离散取值有３个,则用[1,0,0],[0,1,0],[0,0,1]分别表示。缺点:当取值很多时，维度会爆炸，只适用于取值个数少的。

(3)特征嵌入(embedding)

类似于独热编码，将取值映射成某个向量，但是映射后的向量一般不具有可解释性。用独热编码时，特征的取值之间相关性为0，内积为０，当特征的取值有一定关系，可以采用embedding。如生物这个特征，有男人，女人，猫，狗，熊猫，鱼…，显然男人与女人这两个的向量表示相似度要高与男人与猫之间的相似度。同时，embedding可以限定向量的维度，解决独热编码的维度爆炸问题。

3.连续值离散化

作用
(1)对异常数据的鲁棒性
如年龄，把30岁以下为0,30岁以上为1。当有异常值300时，也是1不会对模型带来很多干扰。
(2)模型更稳定，不易过拟合
如20-30岁为一个区间，2,3岁的差值实际没太大影响，若没有离散化，则相差一些，结果就差很多。但是处于区间边界的就会相反，30,31差一岁，但是离散后，两者就会差很多，因此如何确定好区间很重要。
(3)增强非线性，提高模型的表达能力(拟合能力)
当一个连续型特征没有离散化时，模型对该特征就是只有一个权重。离散后，在采用独热编码等，就能将１个特征变为多个特征，此时每个特征取值都有一个权重，引入非线性，模型也复杂了，提高拟合能力。同时可以进行特征的交叉组合，生成更多的特征，进一步引入非线性。

(1)根据阀值进行分组

如将取值的0－0.3分一组，0.3-0.7分一组,0.7-1分一组。

(2)基于聚类分析的方法

根据聚类算法将数据分为多个簇，对应多个区间。

(3)采用决策树模型

通过单特征决策树模型，通过信息增益等，确定取值分区。

4.特征标准化和归一化（数值型特征）

作用
（1)消除特征之间的量纲和取值范围的差异对模型的影响。
（2)有利于梯度下降法的收敛速度

(1)零－均值标准化（Z-score）

(x－均值)/标准差。将数据变成均值为0，方差为1。要求原始数据分布近似符合高斯分布。不会改变每个特征各自的原本的分布，量纲大的列被缩小，量纲小的列被放大，量纲不严格相等，只是消除了一大部分的量纲差异。

(2)归一化

比较简单，把值放缩到某个区间，量纲会严格相等。最大最小值容易受异常值影响

(3)L1/L2范数标准化

求出样本的Ｌ1或L2范数，在将样本的每个特征除以该范数。该方法可以去处特征的量纲。经过该标准化后，样本的欧式距离和余弦相似度是等价的。可以通过计算欧式距离来得到余弦相似独。

如何选择
如果需要进行欧式距离计算，梯度下降等，最好选归一化。若注重取值分布情况，选择标准化。

5.时间类型的数据处理

(1) 连续的时间差值法

以某个时间点为基点(0点)，将时间化为为多少秒或分钟或小时。

(2)将时间转化为离散特征

将时间特征分离成年，月，日，星期，小时，分钟，多个单独离散特征，这对于一些，比如周五有特殊活动的数据比较好。

6.文本类型的数据预处理

离散表示和分布式表示。离散表示是词袋模型（one-hot，TF-IDF,n-gram)，分布式是词嵌入word embedding，经典模型word2vec,Glove，ELMO,GPT,BERT。

(1)词袋

one-hot
将词根据词库转为稀疏向量。通过一个语料库，即文章中所有的词去重后，得到一个n维向量，n为所有词的个数。对于每个样本，样本词对应的语料库位置为1，其他为0，便得到这个样本的表示方式。如词库[a,b,c,d,e,f,g]。样本为adc,则向量表示为[1,0,1,1,0,0,0]。这个方法显然忽略了词的顺序关系，以及词之间的相关性，并且当语料库很大时，向量维度就会变非常大。
TF-IDF
用来评估某个词在文章中的重要性。可以过滤掉文章中的无用词，提取出关键词。
TF:某个词在文章中出现的频率：该文章中出现该词的次数/文章总词数
IDF:逆文档频率，当一个词在很多文章中都出现，则该词不是这篇文章的关键词。
log(语料库文档总数/(包含该词的文档数+1))
最后用TF*IDF表示该词的重要性，从而代替one-hot中用0,1表示。但是仍然存在数据稀疏，维度大，没有考虑字前后信息。
n-gram
2-gram:　原：a,b,c,d,e,f 变为：a,ab,b,bc,c,ce,e,ef,f。多取２个连续字，然后在用one－hot　或TF-IDF进行编码，这种方式前后词就有了联系，但是显然更加加剧了向量维度爆炸。

(1)word embedding

word2vec
将词映射成一个向量，但是映射关系是黑盒。其实就是将词输入到神经网络，得到的输出层的向量就是表示该词的向量，当然这个网络需要先训练，可以设置输出层神经元个数，解决one-hot编码的维度爆炸。同时向量之间的相似度还能表征词之间的相关性。

7.异常特征样本清洗

(1)偏差检测（聚类和k近邻）

用KMeans聚类将训练样本聚成几类，样本数少，且和其他簇离得远的，那么很可能是异常数据

(2)异常点检测(iForest,one class SVM)

iForest:孤立森林，基于Ensemble的快速异常检测方法。应用于连续型数据的异常检测，将异常定义容易被孤立的离群点。思想为将不断对数据根据某一维度进行划分，直到每个小区域只包含一个样本点，则离群点很容易就被划分到单独一个区域，正常样本通常比较密集，需要划分比较多次。
具体步骤：
１．从样本中随机取m个样本，放在树根。
２．随机取某个特征，在当前数据中，该特征最大值和最小值，在中间随机取分割点，对样本划分为两个分支。
３．递归重复２的操作，直到每个样本都单独落入一个叶子节点，或者达到了设定的树的深度。
４．通过１－３的步骤建立n课孤立树，孤立森林建立完成。
５. 将每个训练样本，输入孤立森林，即遍历每课孤立树，看样本落在哪一层，取所有结果平均值，根据设定的阀值，小于该阀值，认定为异常数据。目前算法输出的是一个０－１的值，越接近与１，表明是异常数据的可能性越高。
优点:快，具有线性时间复杂度。每棵树独立建立，可并行。
缺点：仅对全局稀疏点敏感，不擅长处理局部相对稀疏点。不适合维度特别高的数据，因为每次都是随机选择一个特征，很可能树建好后，还有很多特征没用到，导致结果不可靠。
one class svm
思想是，知道正常数据的特征，当一个数据样本不满足正常样本的特征时，就认定是异常数据。方法是，训练一个最小超球面，将正常数据都包含进去，当样本落在该超球面外时，认定不属于正常样本这个类，则属于异常。通常可以用来解决数据样本不均匀的二分类问题。

(3)基于统计的异常点检测

极差，四分位数间距，均值，标准差等，对单值变量进行分析，对每个特征进单独分析。
四分位距通常用来构建箱形图(盒须图，盒式图，盒状图，箱线图)

１.首先对数据进行排序。
2.下四分位数：1*(n＋１)/4,例如14个样本，则计算结果为3.75。
下四分位数=0.25第三项的值＋0.75第四项
3.中位数：最中间的数，如果是偶数，取中间的两个数的平均值
2*(14+1)/4=7.5
中位数＝0.5第七项的值＋0.5第八项的值
4.上四分位数：3*(14+1)/4=11.25
上四分位数＝0.75×第11项的值+0.25第4项的值
5.上限:非异常值的最大值
四分位距＝上四分位数－下四分位数
上限＝四分位距×１.5+上四分位数
6.下限:非异常值的最小值
下限＝下四分位数－1.5四分位距
优点：
1.异常值不会影响箱线图的形状，可以直观明了看出异常值
2.判断数据的偏态和尾重
标准正态分布，异常值少。异常值多时，尾部越重。
异常值集中在较小值侧，则分布呈左偏，反之则亦然。
缺点:
不能精确地衡量数据分布的偏态和尾部程度。

(5)基于密度或距离异常点检测。

通过考察样本点周围的密度，或者和大多数点之的距离，通过阀值进行筛选。

特征选择

1.过滤法选择特征(Filter)

按照特征的发散性或者相关性指标对各个特征进行评分，设定阀值，或排序，选择合适的特征。

(1) 方差筛选法

方差大的特征，认为是比较有用的信息，若值都是相同，则方差为0，该特征就毫无意义。一般特征选择阶段，先用方差筛选过滤一些方差很小的特征。

(2) 相关系数

主要用于连续型输出值。通过计算特征与输出值的相关系数，确定特征与输出的相关性，选择特征。
欧式距离
计算两个向量之间的距离差，以此来表征向量间的相关性，但是变量直接的取值范围不同时,结果不可靠，a的取值0-1，b的取值0-1000，则b变化一点点，结果就差很多，需要先进行归一化。
余弦相似度
cos(a,b) = (ab)/|a||b|，取值-1,1，衡量方向上的相似独。取值为0,说明两者垂直，毫无相关。取值为1,同向正相关，夹角为0,为-1时，负相关，方向完全相反。
皮尔逊相关系数
度量两个变量之间的相关程度(线性相关)。用于服从正态分布的两连续性变量。对异常值特别敏感。
协方差:


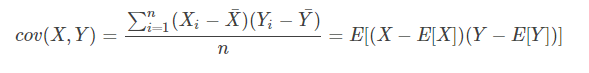
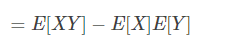
为1表示正相关，-1表示负相关，但是为０表示无线性相关性，但是可能存在其他的相关性。
相关系数:

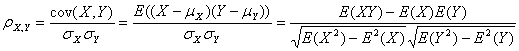
实际上只是标准化后的协方差，剔除了X,Y这两个偏离程度量纲的影响。
普通最小二乘法在相关性大的问题上误差较大。（原因待解）

也相当于先将向量中心化，在进行余弦相似度得到的结果。余弦相似度要求向量每个维度都不能缺失，而皮尔逊相关系数处理缺失值时，采用的是将缺失值补0，在对向量中心化，这样每个维度的均值都是0，缺失值补0的均值也是0。

(3)假设检验法（卡方检验，F检验，t检验）

假设检验衡量自变量取值分布与因变量取值分布的关系。其思想是”小概率事件“原理，即小概率事件在一次试验中基本上不会发生。用于离散变量。

(4)互信息

互信息＝信息熵－条件信息熵。若加入一个特征的信息后，输出的信息熵变小很多多，则说明该特征对输出值影响很大。从信息熵的角度分析各个特征和输出值之间的关系评分。互信息越大，说明该特征和输出值之间相关性大。经典的互相信息一般用于离散类型。

过滤法选特征的缺点:　没有考虑特征之间的关联作用，有可能两个特征单独对输出值没什么影响，但是两个特征一起时，对结果影响很大，如此就可能把有用的关联特征误踢掉。

2.包装法选择特征(Wrapper)

每次选择部分特征，或这排除部分特征，看模型结果的目标函数得分，进行保留或剔除特征。

(1)递归消除特征算法

选择一个基本模型，决策树或者LR，采用PFE框架，将获取特征重要性权值方法嵌入，进行多轮训练，每轮把权重值很小的特征剔除，在根据新的特征进行下一轮训练，逐步剔除不重要的特征。

3.嵌入法选择特征

先用某些机器学习的算法模型训练，得到各个特征的权值系数，根据权值系数大小选择特征。

(1)基于惩罚项的特征选择法

常采用L1正则化和L2正则化。正则化惩罚项越大，特征系数就会越小。随着惩罚项增大，特征系数逐渐减到0,越早减到0的特征,重要性越差,就可以去除。L1,L2正则化采用基学习器是LR。(L1正则降维原理是在保留多个相同相关性的特征中，选择一个，其他没选到的并不代表不重要，可以采用L2进行优化)

(2) 基于树模型的特征选择法

可以采用决策树，gbdt。一般来说只有能得到特征系数或特征重要性的算法才可以作为嵌入法的基学习器。

4.　特征组合

常用方法:特征相加，相减,乘除，平方等，通过根据业务进行特征组合。如有路程和时间，可以得到速度这个组合特征。通常先确定好模型后，在进行特征组合优化。

特征工程－－降维

(1) 主成分分析（PCA）

选择特征投影方差最大的方向，将特征映射到该方向。映射后维度减小，且每一维都失去了原来的物理含义，是原本多维特征变换叠加。无监督降维。

(2) 线性判别分析法(LDA)

LDA是有监督降维，是分类模型。目标找一个投影方向，使得投影后，同一类的方差尽可能小，类与类之间的方差尽可能大。