感知机模型

原创

于 2019-10-24 16:08:48 发布 · 337 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#感知机 #二分类器

本文介绍了感知机作为线性二分类器的基本原理，包括模型表示、感知机学习过程以及点到超平面距离的计算。通过梯度下降法最小化损失函数来确定超平面的参数w和b，进而实现分类。文章还讨论了随机梯度下降在实际应用中的作用，以优化参数更新。

感知机

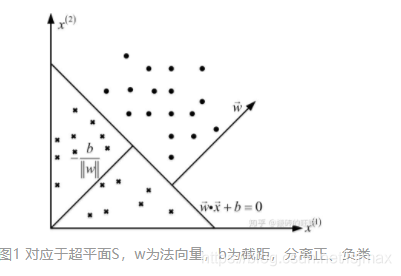
感知机时神经网络的雏形，是线性二分类器，输入实例的特征向量，输出1，-1进行实例的分类。感知机模型是寻找N维空间的超平面。(超平面是指将空间一分为二的平面，N维空间的超平面为N-1维，如二维平面的超平面是一条直线，三维空间的超平面是一个平面)。
感知机模型的表示：
$f(x⃗)=sign(w⃗⋅x⃗+b)f(\vec{x})=sign(\vec{w} \cdot \vec{x}+b)$
其中， $w⃗\vec{w}$ 和b是模型的参数，需要学习的， $w⃗\vec{w}$ 为该超平面 $w⃗⋅x⃗+b=0\vec{w} \cdot \vec{x}+b=0$ 的法向量。
在这里插入图片描述

感知机学习

感知机模型重要就是确定超平面，就是求出 $w⃗,b\vec{w},b$ 这两个参数。方法就是建立一个目标函数，就行迭代求优。该目标函数往往为损失函数(当前模型与实际真实模型的差距)，通过梯度下降，最小化损失函数。
自然容易想到的是，统计训练数据分类分错的样本个数，但是他无法用函数表示，就是无法就行微分，不能用梯度下降。因此采用另一个方法，计算误分类的点到超平面的距离 $d$ ,损失函数就是所有误分类点到超平面的距离的总和。
$L(w⃗,b)=∑diL(\vec{w},b)=\sum d_i$

点到超平面的距离计算

设样本点 $x0⃗\vec{x_0}$ ，在超平面 $w⃗⋅x⃗+b=0\vec{w} \cdot \vec{x}+b=0$ 的投影(作垂线)为 $x1⃗\vec{x_1}$ ,则所求的距离d就是向量 $x0x1⃗\vec{x_0x_1}$ 的模长。显然 $w⃗\vec{w}$ 和 $x0x1⃗\vec{x_0x_1}$ 平行，则有：
$w⃗⋅x0x1⃗=∣w⃗∣∣x0x1⃗∣cos(0orπ)\vec{w}\cdot\vec{x_0x_1}=|\vec{w}| |\vec{x_0x_1}|cos(0 or π)$