【中山纪念中学六年级程序设计思维班模拟赛第三场】修路（rood）

题目描述

有 n 个好朋友，目前任意两个朋友家之间没有任何道路相连，其中第 i 个朋友家对应着修路费用 di，凡是连接到朋友 i 家的道路都要增加 di 的费用，每条道路连接两个朋友家。换句话说，朋友 a 和朋友 b 家之间修一条道路花费的费用为 da+db。现在准备修建一些道路，使得 n 个好朋友家之间是连通的。也就是说，从任意一个朋友家出发能通过修建的道路到达其他朋友家。现在想知道最少需要花费多少费用？

输入

从文件 rood.in 中读入数据。

第一行包含一个正整数 n(1 ≤ n ≤ 100 000)，表示朋友的数量。
第二行包含 n 个正整数 di(1 ≤ di ≤ 10^9),表示朋友 i 家的道路维修费用。两个数之间用一个空格隔开。

输出

输出到文件 rood.out 中。

输出确保 n 个朋友家连通的最少维修费用。

样例数据

输入 #1 复制

样例输入1：
1
10
样例输入2：
3
5 5 5
样例输入3：
4
7 3 3 5

输出 #1 复制

样例输出1:
0
样例解释：因为只有一个朋友，他到自己家是可达的，所以不需要修建道路。
样例输出2：
20
样例输出3：
24
样例解释：可以在1号和2号，2号和3号，3号和4号这三对朋友之间修建道路，所需费用为(7+3)+(3+3)+(3+5)=24。

数据范围限制

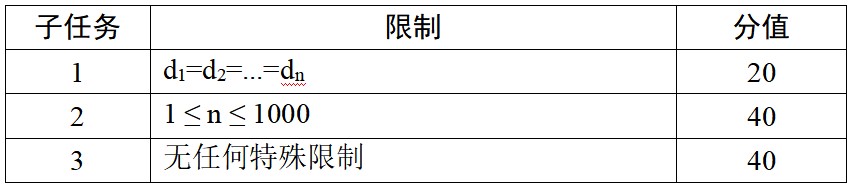
思路：

这道题是个贪心，看起来很吓人，实际上菜的要死，可以选中一个最小值来连接所有的点，其中每个点都要算一遍，最小值算n-1遍，再减去每个点算的最小值，就是n-1个最小值，最后相加并输出就行了。

AC代码：

#include<bits/stdc++.h>
using namespace std;
long long mi=INT_MAX,sum,a;
int n;
int main()
{
	freopen("rood.in","r",stdin);
	freopen("rood.out","w",stdout);	
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&a);
		sum+=a,mi=min(mi,a);
	}
	printf("%lld",(n-2)*mi+sum);
	return 0;
}